(人教版)2021-2022学年度第二学期八年级数学第19章一次函数 期末复习测试卷
试卷更新日期:2022-05-27 类型:复习试卷
一、单选题
-
1. 弹簧挂上物体后会伸长,测得一弹簧的长度y(cm)与所挂的物体的质量x(kg)间有下面的关系:
x/kg
0
1
2
3
4
5
y/cm
10
10.5
11
11.5
12
12.5
下列说法一定错误的是( )
A、x与y都是变量,且x是自变量,y是因变量 B、弹簧不挂重物时的长度为0cm C、物体质量每增加1kg,弹簧长度y增加0.5 cm D、所挂物体质量为7kg时,弹簧长度为13.5cm2. 下列函数中,图象经过原点的是( )A、 B、 C、 D、3. 下列各图中,不能表示y是x的函数的是( )A、 B、
B、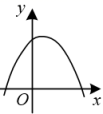 C、
C、 D、
D、 4. 已知正比例函数的图像经过点(2,4)、(1,)、(1,),那么与的大小关系是( )A、 B、 C、 D、无法确定5. 点 、点 在正比例函数 的图像上,当 时,则 与 的大小关系是( )A、 B、 C、 D、无法判断6. 对于函数 (k是常数, ),下列说法错误的是( )A、该函数是正比例函数 B、该函数图象过 C、该函数图象经过二、四象限 D、y随着x的增大而增大7. 如图,一束光线从点A(4,4)发出,经y轴上的点C反射后,经过点B(1,0),则点C的坐标是( )
4. 已知正比例函数的图像经过点(2,4)、(1,)、(1,),那么与的大小关系是( )A、 B、 C、 D、无法确定5. 点 、点 在正比例函数 的图像上,当 时,则 与 的大小关系是( )A、 B、 C、 D、无法判断6. 对于函数 (k是常数, ),下列说法错误的是( )A、该函数是正比例函数 B、该函数图象过 C、该函数图象经过二、四象限 D、y随着x的增大而增大7. 如图,一束光线从点A(4,4)发出,经y轴上的点C反射后,经过点B(1,0),则点C的坐标是( ) A、 B、 C、 D、8. 已知一次函数的图象如图,则不等式的解集为( )
A、 B、 C、 D、8. 已知一次函数的图象如图,则不等式的解集为( ) A、 B、 C、 D、9. 直线y=﹣2x﹣1关于y轴对称的直线与直线y=﹣2x+m的交点在第四象限,则m的取值范围是( )A、m>﹣1 B、m<1 C、﹣1<m<1 D、﹣1≤m≤110. 春节前,某加工厂接到面粉加工任务,要求5天内加工完220吨面粉.加工厂安排甲、乙两组共同完成加工任务.乙组加工中途停工一段时间维修设备,然后提高加工效率继续加工,直到与甲队同时完成加工任务为止.设甲、乙两组各自加工面粉数量y(吨)与甲组加工时间x(天)之间的关系如图所示,结合图象,下列结论错误的是( )
A、 B、 C、 D、9. 直线y=﹣2x﹣1关于y轴对称的直线与直线y=﹣2x+m的交点在第四象限,则m的取值范围是( )A、m>﹣1 B、m<1 C、﹣1<m<1 D、﹣1≤m≤110. 春节前,某加工厂接到面粉加工任务,要求5天内加工完220吨面粉.加工厂安排甲、乙两组共同完成加工任务.乙组加工中途停工一段时间维修设备,然后提高加工效率继续加工,直到与甲队同时完成加工任务为止.设甲、乙两组各自加工面粉数量y(吨)与甲组加工时间x(天)之间的关系如图所示,结合图象,下列结论错误的是( ) A、乙组中途休息了1天 B、甲组每天加工面粉20吨 C、加工3天后完成总任务的一半 D、3.5天后甲乙两组加工面粉数量相等
A、乙组中途休息了1天 B、甲组每天加工面粉20吨 C、加工3天后完成总任务的一半 D、3.5天后甲乙两组加工面粉数量相等二、填空题
-
11. 某市地铁票价计费标准如表所示:乘车距离x(单位:公里):
乘车距离x
x≤6
6<x≤12
12<x≤22
22<x≤32
x>32
票价(元)
3
4
5
6
每增加1元可乘20公里
另外,使用市政交通一卡通,每个自然月每张卡片支出累计满100元后,超出部分打8折;满150元后,超出部分打5折;支出累计达400元后,不再打折.小红妈妈上班时,需要乘坐地铁15公里到达公司,每天上下班共乘坐两次,如果每次乘坐地铁都使用市政交通一卡通,那么每月第22次乘坐地铁上下班时,她刷卡支出的费用是元.
12. 已知正比例函数的图象经过第一、三象限,且经过点(k,k+2),则k= .13. 已知一次函数的图象向上平移b个单位后经过第一象限,请你写出一个符合条件的b的值为 .14. 如图,函数y=2x和y=ax+4的图象相交于点A(n,2),则不等式2x≥ax+4的解集为 . 15. 河北给武汉运送抗疫物资,某汽车油箱内剩余油量Q(升)与汽车行驶路程s(千米)有如下关系:
15. 河北给武汉运送抗疫物资,某汽车油箱内剩余油量Q(升)与汽车行驶路程s(千米)有如下关系:行驶路程s(千米)
0
50
100
150
200
…
剩余油量Q(升)
40
35
30
25
20
…
则该汽车每行驶100千米的耗油量为 升.
三、解答题
-
16. 物体从高处自由下落的高度h(m)与物体下落的时间t(s)之间的函数关系式是:h= gt2(g表示重力加速度,g取9.8m/s2).某人发现头顶上空490m处有一炸弹自由下落,其地面杀伤半径为50m,此人发现后,立即以6m/s的速度逃离,那么此人有无危险?17. 请在图中画出直线 的图象,并且直线与 轴、 轴交点分别为 ,若直线 上的点 在第一象限,且 ,求点 的坐标.
 18. 已知正比例函数y=kx经过点A,点A在第四象限,过点A作AH⊥x轴,垂足为点H,点A的横坐标为3,且△AOH的面积为3.
18. 已知正比例函数y=kx经过点A,点A在第四象限,过点A作AH⊥x轴,垂足为点H,点A的横坐标为3,且△AOH的面积为3.(1)求正比例函数的解析式;
(2)在x轴上能否找到一点P,使△AOP的面积为5?若存在,求点P的坐标;若不存在,请说明理由.
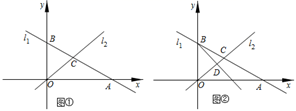
19. 已知 与 成正比例,且当 时, .(1)、求 与 之间的函数表达式;(2)、当 时,求 的值.20. 在平面直角坐标系中,直线 : 分别与x轴、y轴交于点A、点B,且与直线 : 于点C.Ⅰ 如图 ,求出B、C两点的坐标;
Ⅱ 若D是线段OC上的点,且 的面积为4,求直线BD的函数解析式.
Ⅲ 如图 ,在 Ⅱ 的条件下,设P是射线BD上的点,在平面内是否存在点Q,使以O、B、P、Q为顶点的四边形是菱形?若存在,直接写出点Q的坐标;若不存在,请说明理由.
 21. 如图,直线 分别与x轴,y轴交于A、B两点,A、B的坐标分别为 、 ,过点B的直线 交x轴于点C , 点 是直线l上的一点,连接 .
21. 如图,直线 分别与x轴,y轴交于A、B两点,A、B的坐标分别为 、 ,过点B的直线 交x轴于点C , 点 是直线l上的一点,连接 .
(Ⅰ)求 的解析式;
(Ⅱ)求C、D的坐标;
(Ⅲ)求 的面积.