(人教版)2021-2022学年度第二学期八年级数学19.2一次函数 期末复习测试卷
试卷更新日期:2022-05-27 类型:复习试卷
一、单选题
-
1. 在正比例函数y=kx中,y的值随着x值的增大而减小,则点A(﹣3,k)在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限2. 已知正比例函数y=(2m﹣6)x的图象上一点(x0 , y0),且<0,则m的取值范围是( )A、m>3 B、m> C、m< D、m<33. 一个正比例函数的图象经过点A(﹣2,3)点B(a,﹣3),则a的值是( )A、2 B、﹣2 C、 D、﹣4. 已知一次函数 ,y随x的增大而减小,则m的值可能是( )A、1 B、2 C、3 D、55. 把直线y=3x-2向上平移2单位长度后,其直线解析式为( )A、y=3x-4 B、y=-3x-4 C、y=3x D、y=3x+46. 如图,一次函数y=2x+3的图像交y轴于点A,交x轴于点B,点P在线段AB上(不与A,B重合),过点P分别作OB和OA的垂线,垂足分别为C,D.当矩形OCPD的面积为1时,点P的坐标为( )
 A、 B、(-1,1) C、 或(-1,1) D、不存在7. 如图,在平面直角坐标系中,直线 分别交x轴,y轴于点A,点B,线段AB上有一点C,点C的横坐标为 ,过点C的直线 与直线AB垂直,交y轴于点D,则不等式 的所有负整数解的和是( )
A、 B、(-1,1) C、 或(-1,1) D、不存在7. 如图,在平面直角坐标系中,直线 分别交x轴,y轴于点A,点B,线段AB上有一点C,点C的横坐标为 ,过点C的直线 与直线AB垂直,交y轴于点D,则不等式 的所有负整数解的和是( )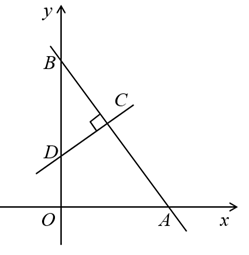 A、-10 B、-6 C、-3 D、-18. 甲、乙两辆遥控车沿直线AC作同方向的匀速运动.甲、乙同时分别从A,B出发,沿轨道到达C处.已知甲的速度是乙的速度的1.5倍,设t分钟后甲、乙两车与B处的距离分别为S1 , S2 , 函数关系如图所示.当两车的距离小于10米时,信号会产生相互干扰.那么t是下列哪个值时两车的信号会相互干扰( )
A、-10 B、-6 C、-3 D、-18. 甲、乙两辆遥控车沿直线AC作同方向的匀速运动.甲、乙同时分别从A,B出发,沿轨道到达C处.已知甲的速度是乙的速度的1.5倍,设t分钟后甲、乙两车与B处的距离分别为S1 , S2 , 函数关系如图所示.当两车的距离小于10米时,信号会产生相互干扰.那么t是下列哪个值时两车的信号会相互干扰( ) A、 B、2 C、 D、9. 一次函数y= kx+b的图象过点P (2,8),且分别与x轴和y轴的正半轴交于A,B两点,点O为坐标原点.当△AOB面积最小时,则k+b的值为( )A、10 B、12 C、14 D、1610. 如图,一束光线从点出发,经轴上的点反射后经过点 , 则点的坐标是( )
A、 B、2 C、 D、9. 一次函数y= kx+b的图象过点P (2,8),且分别与x轴和y轴的正半轴交于A,B两点,点O为坐标原点.当△AOB面积最小时,则k+b的值为( )A、10 B、12 C、14 D、1610. 如图,一束光线从点出发,经轴上的点反射后经过点 , 则点的坐标是( )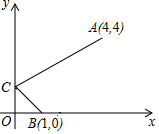 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 已知正比例函数的图象上有两点、 , 若 , 则与的大小关系是.12. 已知点A的坐标是 , 点B是正比例函数 的图象上一点,若只存在唯一的点B,使 为等腰三角形,则k的取值范围是.13. 直线y=x+4与x轴、y轴分别交于点A和点B,在x轴上取点C,使△ABC为等腰三角形,则点C的坐标是 .14. 如果一次函数y = kx + b(k≠0)中两个变量x,y的部分对应值如下表所示:那么关于x的不等式kx + b≥8的解集是 .
x
-3
-2
-1
0
1
y
11
8
5
2
-1
15. 若函数的图象经过点 , 其图像如图所示,则关于x的不等式的解集为 .
三、解答题
-
16. 如图,已知正比例函数y=kx经过点A , 点A在第四象限,过点A作AH⊥x轴,垂足为点H , 点A的横坐标为3,且△AOH的面积为3.求正比例函数的表达式.
 17. 已知正比例函数y=kx的图像经过第四象限内一点 ,求k的值.18. 某某鲜花销售公司每月付给销售人员的工资有两种方案.
17. 已知正比例函数y=kx的图像经过第四象限内一点 ,求k的值.18. 某某鲜花销售公司每月付给销售人员的工资有两种方案.方案一:没有底薪,只付销售提成;
方案二:底薪加销售提成.
如图中的射线l1 , 射线l2分别表示该鲜花销售公司每月按方案一,方案二付给销售人员的工资y1(单位:元)和y2(单位:元)与其当月鲜花销售量x(单位:千克)(x≥0)的函数关系.分别求y1、y2与x的函数解析式(解析式也称表达式).
 19. 如图,一次函数y=﹣2x+3的图象交x轴于点A,交y轴于点B,点P在线段AB上(不与点A,B重合),过点P分别作OA和OB的垂线,垂足为C,D.当矩形OCPD的面积为1时,求此时P点的坐标.
19. 如图,一次函数y=﹣2x+3的图象交x轴于点A,交y轴于点B,点P在线段AB上(不与点A,B重合),过点P分别作OA和OB的垂线,垂足为C,D.当矩形OCPD的面积为1时,求此时P点的坐标. 20. 如图,过点的直线:与直线:交于点.求k,b,m的值.
20. 如图,过点的直线:与直线:交于点.求k,b,m的值. 21. 学完《一次函数》后,老师布置了这样一道思考题:如图,在中, , , , , 和相交于点P.求的面积.
21. 学完《一次函数》后,老师布置了这样一道思考题:如图,在中, , , , , 和相交于点P.求的面积.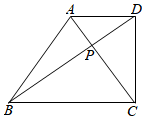
小明同学应用所学知识,顺利地解决了此题,他的思路是这样的:建立适当的“平面直角坐标系”,写出图中一些点的坐标.根据“一次函数”的知识求出点的坐标,从而可求得的面积.请你按照小明的思路解决这道思考题.

