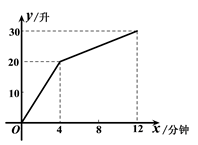(人教版)2021-2022学年度第二学期八年级数学19.1变量与函数 期末复习测试卷
试卷更新日期:2022-05-27 类型:复习试卷
一、单选题
-
1. 如图,正方形ABCD的边长是4,E是AB上一点,F是延长线上的一点,且BE=DF,四边形AEGF是矩形,设BE的长为x,AE的长为y,矩形AEGF的面积为S,则y与x,S与x满足的函数关系分别是( )
 A、一次函数关系,二次函数关系 B、反比例函数关系,二次函数关系 C、一次函数关系,反比例函数关系 D、反比例函数关系,一次函数关系2. 为预防传染病,某校定期对教室进行“药熏消毒”测出药物燃烧阶段室内每立方米空气中的含药量y(mg)和燃烧时间x(min)的数据如表:
A、一次函数关系,二次函数关系 B、反比例函数关系,二次函数关系 C、一次函数关系,反比例函数关系 D、反比例函数关系,一次函数关系2. 为预防传染病,某校定期对教室进行“药熏消毒”测出药物燃烧阶段室内每立方米空气中的含药量y(mg)和燃烧时间x(min)的数据如表:燃烧时间x(min)
2.5
5
7.5
10
含药量y(mg)
2
4
6
8
则下列叙述错误的是( )
A、燃烧时间为14min时,室内每立方米空气中的含药量为10mg B、在一定范围内,燃烧时间越长,室内每立方米空气中的含药量越大 C、室内每立方米空气中的含药量是因变量 D、燃烧时间每增加2.5min,室内每立方米空气中的含药量增加2mg3. 如果每盒水笔有10支,售价16元,用(元)表示水笔的售价,表示水笔的支数,那么与之间的关系应该是( )A、 B、 C、 D、4. 在函数中x的取值范围是( )A、 B、 C、 D、5. 已知函数 , 则自变量的取值范围是( )A、 B、﹣1且 C、 D、6. 一辆公共汽车从车站开出,加速行驶一段后开始匀速行驶,过了一段时间,汽车到达下一个车站.乘客上、下车后汽车开始加速,一段时间后又开始匀速行驶,下面哪幅图可以近似地刻画出汽车在这段时间内的速度变化情况( )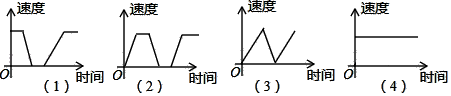 A、第(1)幅图 B、第(2)幅图 C、第(3)幅图 D、第(4)幅图7. 用表示a、b两数中较大的数,如 . 若函数y=max{1,(x>0)},则y与x之间的函数图象大致为( )A、
A、第(1)幅图 B、第(2)幅图 C、第(3)幅图 D、第(4)幅图7. 用表示a、b两数中较大的数,如 . 若函数y=max{1,(x>0)},则y与x之间的函数图象大致为( )A、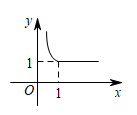 B、
B、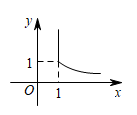 C、
C、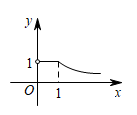 D、
D、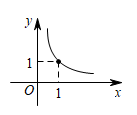 8. 对于关系式y=3x+5,下列说法:①x是自变量,y是因变量;②x的数值可以任意选择;③y是变量,它的值与x无关;④这个关系式表示的变量之间的关系不能用图象表示;⑤y与x的关系还可以用表格和图象表示,其中正确的是( )A、①②③ B、①②④ C、①③⑤ D、①②⑤9. 如图,菱形ABCD的边长为2cm,其中∠A=60°,动点E,F同时从点A都以1cm/s的速度出发,点E沿A→B→C路线,点F沿A→D→C路线运动。连接EF.设运动时间为ts,△AEF的面积为Scm2 , 则下列图象中能大致表示S与t的函数关系的是( )
8. 对于关系式y=3x+5,下列说法:①x是自变量,y是因变量;②x的数值可以任意选择;③y是变量,它的值与x无关;④这个关系式表示的变量之间的关系不能用图象表示;⑤y与x的关系还可以用表格和图象表示,其中正确的是( )A、①②③ B、①②④ C、①③⑤ D、①②⑤9. 如图,菱形ABCD的边长为2cm,其中∠A=60°,动点E,F同时从点A都以1cm/s的速度出发,点E沿A→B→C路线,点F沿A→D→C路线运动。连接EF.设运动时间为ts,△AEF的面积为Scm2 , 则下列图象中能大致表示S与t的函数关系的是( )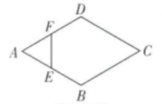 A、
A、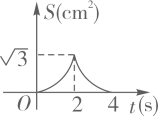 B、
B、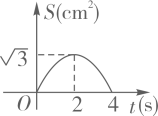 C、
C、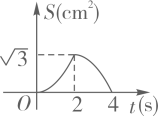 D、
D、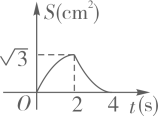 10. 一列货运火车从某站出发,加速行驶一段时间后开始匀速行驶,过了一段时间,火车到达下一个车站停下,装完货后,火车又加速行驶,一段时间后再次开始匀速行驶,那么可以近似地刻画出火车在这段时间内的速度变化情况的是( )A、
10. 一列货运火车从某站出发,加速行驶一段时间后开始匀速行驶,过了一段时间,火车到达下一个车站停下,装完货后,火车又加速行驶,一段时间后再次开始匀速行驶,那么可以近似地刻画出火车在这段时间内的速度变化情况的是( )A、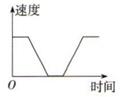 B、
B、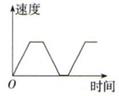 C、
C、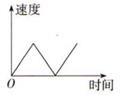 D、
D、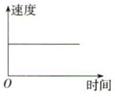
二、填空题
-
11. 在函数 中,自变量x的取值范固是 .12. 已知f(x)=x3 -1, 那么f(2)=13. 一个边长为2厘米的正方形,如果它的边长增加 厘米,则面积随之增加y平方厘米,那么y关于x的函数解析式为.14. 有边长为1的小等边三角形卡片若干张,使用这些三角形卡片拼出边长为2、3、4、……的大等边三角形(如图所示).
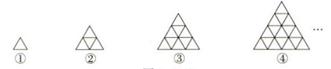
根据图形推断,每个大等边三角形所用的小等边三角形的卡片数S与大等边三角形的边长n的关系式是
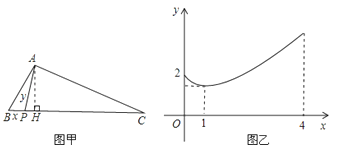
15. 如图,甲,乙两个工程队完成某项工程,首先是甲单独做了 天,然后乙队加入合做,完成剩下的全部工程.设工程总量为单位 ,工程进度满足如图所示的函数关系,设 甲的工作效率:乙的工作效率,则 的值为.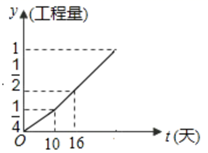
三、解答题
-
16. 已知 , 与 成反比例, 与 成正比例,并且当 时, ;当 时, .求:y关于x的函数解析式.17. 如图,正方形ABCD的边长为4cm,E,F分别是BC,CD边上一动点,点E,F同时从点C出发,以每秒2cm的速度分别向点B,D运动,当点E与点B重合时,运动停止,设运动时间为x(s),运动过程中△AEF的面积为y(cm2),求y关于x的函数表达式,并写出自变量x的取值范围.
 18. 在平面直角坐标系中,O为原点,点A(6,0),点B在y轴的正半轴上,∠ABO=30°.矩形CODE的顶点D , E , C分别在OA , AB , OB上,OD=2.
18. 在平面直角坐标系中,O为原点,点A(6,0),点B在y轴的正半轴上,∠ABO=30°.矩形CODE的顶点D , E , C分别在OA , AB , OB上,OD=2.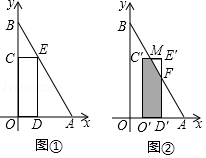
(Ⅰ)如图①,求点E的坐标;
(Ⅱ)将矩形CODE沿x轴向右平移,得到矩形C′O′D′E′,点C , O , D , E的对应点分别为C′,O′,D′,E′.设OO′=t , 矩形C′O′D′E′与△ABO重叠部分的面积为S .
①如图②,当矩形C′O′D′E′与△ABO重叠部分为五边形时,C′E′,E′D′分别与AB相交于点M , F , 试用含有t的式子表示S , 并直接写出t的取值范围;
②当 ≤S≤5 时,求t的取值范围(直接写出结果即可).
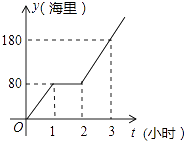
19. 为了增强居民的节水意识,某城区水价执行“阶梯式”计费,每月应缴水费y(元)与用水量x(t)之间的函数关系如图所示.若某用户去年5月缴水费18.05元,求该用户当月用水量.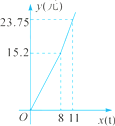 20. 某天早晨,王老师从家出发,骑摩托车前往学校,途中在路旁一家饭店吃早餐,如图所示的是王老师从家到学校这一过程中行驶路程s(千米)与时间t(分)之间的关系.
20. 某天早晨,王老师从家出发,骑摩托车前往学校,途中在路旁一家饭店吃早餐,如图所示的是王老师从家到学校这一过程中行驶路程s(千米)与时间t(分)之间的关系.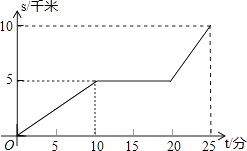 (1)、学校离他家多远?从出发到学校,用了多少时间?(2)、王老师吃早餐用了多少时间?(3)、王老师吃早餐以前的速度快还是吃完早餐以后的速度快?最快时速达到多少?21.
(1)、学校离他家多远?从出发到学校,用了多少时间?(2)、王老师吃早餐用了多少时间?(3)、王老师吃早餐以前的速度快还是吃完早餐以后的速度快?最快时速达到多少?21.一个装有进水管和出水管的容器,从某时刻开始的4分钟内只进水不出水,在随后的8分钟内既进水又出水,接着关闭进水管直到容器内的水放完.假设每分钟的进水量和出水量是两个常数,容器内的水量y(单位:升)与时间x(单位:分钟)之间的部分关系如图象所示.求从关闭进水管起需要多少分钟该容器内的水恰好放完.