（人教版）2021-2022学年度第二学期八年级数学第18章平行四边形 期末复习测试卷
试卷更新日期：2022-05-27 类型：复习试卷
一、单选题
-
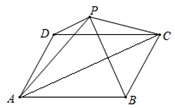
1. 如图，点P为▱ABCD外一点，连接PA、PB、PC、PD，若△APB的面积为18，△APD的面积为5，则△APC的面积为（ ）
A、10 B、13 C、18 D、202. 在▱ABCD中，若 ，则 的度数为（ ）A、100° B、130° C、140° D、150°3. 如图，四边形ABCD的对角线AC，BD交于点O，则不能判断四边形ABCD是平行四边形的是（ ）
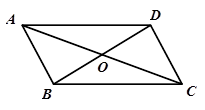A、∠ABD＝∠BDC，OA＝OC B、∠ABC＝∠ADC，AB＝CD C、AD∥BC，OB=OD D、∠ABD＝∠BDC，∠ADB＝∠CBD4. 如图，△ABC的面积为24，点D为AC边上的一点，延长BD交BC的平行线AG于点E，连结EC， 以DE、EC为邻边作平行四边形DECF，DF交BC边于点H，连结AH，当 时，则△AHC的面积为（ ）
A、4 B、6 C、 D、5. 如图，在Rt△ABC中，∠ACB = 90°，CE是斜边AB上的中线，BD⊥CE于点D，过点A作AF⊥CE交CE延长线于点F．下列结论不一定成立的是（ ）
A、∠BAC = ∠DBC B、tan ∠ECB C、AF = BD D、CE = CB6. 如图，点O是▱ABCD的对角线的交点， ， 点E，F分别是OC，OD的中点，过点F作交边AB于点P，连接PE．则下列结论中不一定正确的是（ ）
A、 B、 C、 D、7. 如图，矩形ABCD中，AC，BD相交于点O，过点B作 交CD于点F，交AC于点M，过点D作 交AB于点E，交AC于点N，连接FN，EM.则下列结论：① ；② ：③ ；④当 时，四边形DEBF是菱形.其中，正确结论的个数是（ ）
A、1 B、2 C、3 D、48. 如图，已知点O是矩形ABCD的对称中心，且AB＞AD.点E从点A出发沿AB向点B运动，移动到点B停止，延长EO交CD于点F，则四边形AECF的形状不可能是（ ）
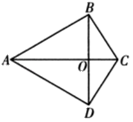
A、平行四边形 B、菱形 C、矩形 D、正方形9. 如图，在正方形ABCD中，点P在对角线BD上，PE⊥BC，PF⊥CD，E、F分别为垂足，连接AP、EF．则下列命题：①若AP=3，则EF=3；②若AP⊥BD，则EF∥BD；③若正方形的边长为4，则EF的最小值为2．其中正确的命题有（ ）
A、0个 B、1个 C、2个 D、3个10. 如图，在四边形ABCD中， ， ， AC，BD交于点O．关于四边形ABCD的形状，甲、乙、丙三人的说法如下：甲：若添加“”，则四边形ABCD是菱形；
乙：若添加“”，则四边形ABCD是矩形；
丙：若添加“”，则四边形ABCD是正方形．
则说法正确的是（ ）
A、甲、乙 B、甲、丙 C、乙、丙 D、甲、乙、丙二、填空题
-
11. 如图，在平行四边形ABCD中，∠BAD的平分线交BC于点E．若AB=6cm，AD=9cm，则EC=cm.
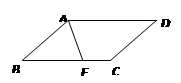12. 如图，已知平行四边形对角线 、 相交于点O，点E、F分别是线段 、 的中点.若 ， 的周长是 ，则 .
13. 如图，▱AFDE的顶点F在矩形ABCD的边BC上，点F与点B、C不重合，若△AED的面积为4，则图中阴影部分两个三角形的面积和为.
14. 如图，在菱形中，对角线 ， 相交于点O， ， ， ， 交于点E，则的长为 ．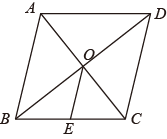
15. 如图，在正方形ABCD中，E为对角线BD上一点，且 ，则 的值为.
三、解答题
-
16. 如图，四边形ABCD是平行四边形，E，F是对角线AC的三等分点，连接BE，DF．证明BE=DF．
17. 如图，在平行四边形ABCD中，点M、N分别是AD、BC上的两点，点E、F在对角线BD上，且DM＝BN，BE＝DF.求证：四边形MENF是平行四边形.
18. 如图，△ABC是锐角三角形，分别以AB，AC为边向外侧作等腰△ABM和等腰△CAN，AM=AB AC=AN，∠MAB=∠CAN.D，E，F分别是MB，BC，CN的中点，连结DE，EF.求证：DE=EF。
19. 如图所示，BD为矩形ABCD的一条对角线，延长BC至点E，使CE=BD，连结AE，若AB=1，∠AEB=15°，求AD的长度.
20. 如图，在矩形ABCD中，E，F为BC上两点，且BE=CF，连结AF，DE交于点O.求证：AF=DE.
