(人教版)2021-2022学年度第二学期八年级数学第18.2特殊的平行四边形 期末复习测试卷
试卷更新日期:2022-05-27 类型:复习试卷
一、单选题
-
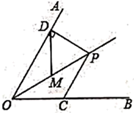
1. 如图, , 是 角平分线上一点, ,垂足为 ,点 是 的中点,且 ,如果点 是射线 上一个动点,则 的最小值是( )
 A、8 B、6 C、4 D、22. 如图,在Rt△ABC中,∠ACB=90°,D、E分别是AB、AC的中点,连接CD、DE,过E作EF∥DC交BC的延长线于F,若△ABC的周长是14,AC的长为4,则四边形CDEF的周长是( )
A、8 B、6 C、4 D、22. 如图,在Rt△ABC中,∠ACB=90°,D、E分别是AB、AC的中点,连接CD、DE,过E作EF∥DC交BC的延长线于F,若△ABC的周长是14,AC的长为4,则四边形CDEF的周长是( ) A、7 B、8 C、10 D、143. 如图,点是矩形的对角线上的点,点 , 分别是 , 的中点,连接 , .若 , , 则的最小值为( )
A、7 B、8 C、10 D、143. 如图,点是矩形的对角线上的点,点 , 分别是 , 的中点,连接 , .若 , , 则的最小值为( ) A、 B、2 C、 D、4. 如图菱形ABCD中, , ,则该菱形的周长为( )
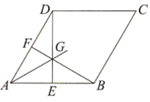
A、 B、2 C、 D、4. 如图菱形ABCD中, , ,则该菱形的周长为( ) A、 B、16 C、 D、85. 如图,在边长为 的菱形 中, ,点E,F分别为折线 上的点(不含菱形顶点), , 、 相交于点G,作射线 .甲、乙二人分别对这个问题进行了研究:
A、 B、16 C、 D、85. 如图,在边长为 的菱形 中, ,点E,F分别为折线 上的点(不含菱形顶点), , 、 相交于点G,作射线 .甲、乙二人分别对这个问题进行了研究:甲:射线 不一定经过点C;
乙:当 垂直于菱形的边时,线段 的长可能为3.
下列判断正确的为( )
 A、甲、乙都对 B、甲、乙都错 C、甲对,乙错 D、甲错,乙对6. 如图,在菱形 中, ,对角线 、 相交于点O,E为 中点,则 的度数为( )
A、甲、乙都对 B、甲、乙都错 C、甲对,乙错 D、甲错,乙对6. 如图,在菱形 中, ,对角线 、 相交于点O,E为 中点,则 的度数为( ) A、70° B、65° C、55° D、35°7. 如图,菱形的边长为6, , 对角线与相交于点O,点E在上,且 , 则线段的长度为( )
A、70° B、65° C、55° D、35°7. 如图,菱形的边长为6, , 对角线与相交于点O,点E在上,且 , 则线段的长度为( ) A、2 B、3 C、 D、8. 如图所示,O为正方形ABCD的中心,BE平分∠DBC,交DC于点E,延长BC到F,使FC=EC,连结DF交BE的延长线于点H,连结OH交DC于点G,连结HC,则下列结论:①OH∥BF;②∠CHF=45°;③GH= BC;④三角形BDF是直角三角形.其中正确的个数是( )
A、2 B、3 C、 D、8. 如图所示,O为正方形ABCD的中心,BE平分∠DBC,交DC于点E,延长BC到F,使FC=EC,连结DF交BE的延长线于点H,连结OH交DC于点G,连结HC,则下列结论:①OH∥BF;②∠CHF=45°;③GH= BC;④三角形BDF是直角三角形.其中正确的个数是( )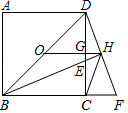 A、1个 B、2个 C、3个 D、4个9. 将正方形ABCD与正方形BEFG按如图方式放置,点F、B、C在同一直线上.已知BG = ,BC = 3,连接DF.M是DF的中点,连接AM,则AM的长是( )
A、1个 B、2个 C、3个 D、4个9. 将正方形ABCD与正方形BEFG按如图方式放置,点F、B、C在同一直线上.已知BG = ,BC = 3,连接DF.M是DF的中点,连接AM,则AM的长是( ) A、 B、 C、 D、10. 勾股定理是中国几何的根源,中华数学的精髓,诸如开方术、方程术、天元术等技艺的诞生与发展,寻根探源,都与勾股定理有着密切关系,在一次数学活动中,数学小组发现如下图形:在中, , 图中以AB、BC、AC为边的四边形都是正方形,并且经测量得到三个正方形的面积分别为225、400、S,则S的值为( )
A、 B、 C、 D、10. 勾股定理是中国几何的根源,中华数学的精髓,诸如开方术、方程术、天元术等技艺的诞生与发展,寻根探源,都与勾股定理有着密切关系,在一次数学活动中,数学小组发现如下图形:在中, , 图中以AB、BC、AC为边的四边形都是正方形,并且经测量得到三个正方形的面积分别为225、400、S,则S的值为( )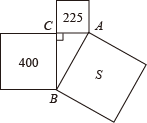 A、25 B、175 C、600 D、625
A、25 B、175 C、600 D、625二、填空题
-
11. 如图,在Rt△ABC中,∠C=90°,AC=6,BC=2,点P是AB边上的一点(异于A,B两点),过点P分别作AC,BC边的垂线,垂足分别为M,N,连接MN,则MN的最小值是 .
 12. 如图,在中,对角线AC、BD相交于点O,OA=OB,若AD=4,∠AOD=60°,则AB的长为 .
12. 如图,在中,对角线AC、BD相交于点O,OA=OB,若AD=4,∠AOD=60°,则AB的长为 . 13. 如图四边形ABCD是菱形,AC=16,DB=12,DH⊥AB于点H,则DH=。
13. 如图四边形ABCD是菱形,AC=16,DB=12,DH⊥AB于点H,则DH=。 14. 如图,在正方形ABCD的外侧,作等边三角形ADE,则∠AEB=度。
14. 如图,在正方形ABCD的外侧,作等边三角形ADE,则∠AEB=度。 15. 在正方形ABCD中,点E在边CD上, , 点F是正方形边上一点, , 则的值为 .
15. 在正方形ABCD中,点E在边CD上, , 点F是正方形边上一点, , 则的值为 .三、解答题
-
16. 如图,△ABC中,BD、CE是△ABC的两条高,点F、M分别是DE、BC的中点.求证:FM⊥DE。
 17. 如图,矩形ABCD的两条对角线相交于点O, , .求矩形的对角线长.
17. 如图,矩形ABCD的两条对角线相交于点O, , .求矩形的对角线长. 18. 如图,Rt△ABC中,AC>BC,∠ACB=90°,CD是△ABC的中线,点E在CD上,且∠AED=∠B,求证:AE=BC.
18. 如图,Rt△ABC中,AC>BC,∠ACB=90°,CD是△ABC的中线,点E在CD上,且∠AED=∠B,求证:AE=BC. 19. 如图,在菱形ABCD中,E为AB上一点,延长BC至点F,使CF=BE,连接CE、DF,求证CE=DF.
19. 如图,在菱形ABCD中,E为AB上一点,延长BC至点F,使CF=BE,连接CE、DF,求证CE=DF. 20. 已知菱形ABCD,E,F分别为菱形外的两点,且E,C,F三点共线,EF交AB于G,连接AE,DE,DF, , . 求证: .
20. 已知菱形ABCD,E,F分别为菱形外的两点,且E,C,F三点共线,EF交AB于G,连接AE,DE,DF, , . 求证: .