（人教版）2021-2022学年度第二学期八年级数学第18.1平行四边形 期末复习测试卷
试卷更新日期：2022-05-27 类型：复习试卷
一、单选题
-
1. 在平行四边形ABCD中，对角线AC与BD交于点O，∠DAC＝40°，∠CBD＝25°，则∠COD等于（ ）
A、60° B、65° C、70° D、75°2. 在▱ABCD中，∠A：∠B＝7：2，则∠C的度数是（ ）A、40° B、70° C、105° D、140°3. 在平行四边形ABCD中，∠A=100°，则∠C=（ ）A、80° B、90° C、100° D、120°4. 如图，平行四边形 中， ，点 在 上，且 ，则 的度数是（ ）
A、 B、 C、 D、5. 平行四边形一定具有的性质是（ ）A、内角和为180° B、是中心对称图形 C、邻边相等 D、对角互补6. 如图，四边形ABCD中，AB∥CD，AB＝5，DC＝11，AD与BC的和是12，点E、F、G分别是BD、AC、DC的中点，则△EFG的周长是（ ）
A、8 B、9 C、10 D、127. 如图，四边形ABCD的对角线AC，BD交于点O，则不能判断四边形ABCD是平行四边形的是（ ）
A、∠ABD=∠BDC，OA=OC B、∠ABC=∠ADC，AD∥BC C、∠ABC=∠ADC，AB=CD D、∠ABD=∠BDC，∠BAD=∠DCB8. 如图，在平行四边形ABCD中，AB＝5，BC＝8，∠ABC和∠BCD的角平分线分别交AD于点E和F，若BE＝6，则CF＝（ ）
A、6 B、8 C、10 D、139. 如图，△ABC是等边三角形，P是三角形内一点，PD∥AB，PE∥BC，PF∥AC，若△ABC的周长为24，则PD+PE+PF＝（ ）
A、8 B、9 C、12 D、1510. 如图，在四边形ABCD中，点E、F分别为AD、DC的中点，连接EB、BF、EF，△EBF的面积为 ．点G为四边形ABCD外一点，连接AG、BG、EG、FG，使得AG＝BC，∠GAB＝∠ABC，△EGF的面积为 ，则 与 满足的关系是（ ）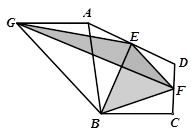
A、 = B、2 =3 C、3 =4 D、3 =2二、填空题
-
11. 如图，在▱ ABCD中，用直尺和圆规作∠BAD的平分线AE交BC于点E，若BF=8，EB=6，则AE的长为 ．
12. 在▱ABCD中，AB，BC，CD的长度分别为2x＋1，3x，x＋4，则▱ABCD的周长是.13. 如图，△ABC中，BD平分∠ABC，且AD⊥BD，E为AC的中点，AD=6cm，BD=8cm，BC=16cm，则DE的长为cm。
14. 如图，▱ABCD的顶点C在等边 的边BF上，点E在AB的延长线上，G为DE的中点，连接CG．若AD=5，AB=CF=3，则CG的长为 ．
15. 如图， ， ， P是OA上一动点（点P不与O、A重合），过点P做 ， ， 交OD于点B，交AD于点C，M是OP中点，N是PA中点连接BM、CN，下列结论正确的是（填写所有正确结论的序号）①是等腰三角形②③四边形是平行四边形，周长是14cm④动点无论移动到OA上哪一点（P不与O、A重合），的值为固定值是.
三、解答题
-
16. 如图，在平行四边形ABCD中，点E，点F在直线BD上，且 ，连接AF，CE，求证 ．
17. 如图，四边形ABCD是平行四边形，延长AB至点E．使BE = AB．连接DE交BC于点F．求证：CF = BF．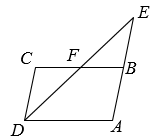
18. 如图，在▱ABCD中，AD=2AB，E为AD的中点，求证：BE平分∠ABC．
19. 如图，在中，∠BAD，∠BCD的平分线分别交对角线BD于点E，F，求证：AE＝CF．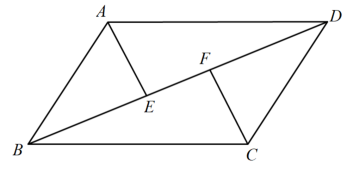
20. 如图，在△ABC中BC>AC，点D在BC上，且DC=AC，∠ACB的平分线CF交AD于F，点E是AB的中点，求证：EF∥BC
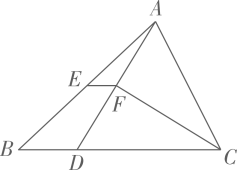21. 如图，在平行四边形ABCD中，E、F分别为边AB、CD的中点.求证：DE BF.
