（人教版）2021-2022学年度第二学期八年级数学第17章勾股定理期末复习测试卷

试卷更新日期：2022-05-27 类型：复习试卷

进入出卷网下载

一、单选题

1. 如图，一圆柱高8cm，底面半径为 $\frac{6}{π}$ cm，一只蚂蚁从点A沿圆柱侧面爬到点B处吃食，要爬行的最短路程是（）

A、6cm B、8cm C、10cm D、12cm

查看试题解析
2. 如图，点P是以A为圆心，AB为半径的圆弧与数轴的交点，则数轴上点P表示的实数是（）

A、-2 B、-2.2 C、 $\sqrt{10}$ D、1- $\sqrt{10}$

查看试题解析
3. 如图，以正方形ABCD的边AD为直径作一个半圆，点M是半圆上一个动点，分别以线段AM、DM为边各自向外作一个正方形，其面积分别为S₁和S₂ ，若正方形的面积为10，随点M的运动S₁＋S₂的值（）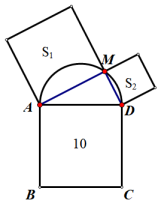

A、大于10 B、小于10 C、等于10 D、不确定

查看试题解析
4. 如图，在 $3 \times 1$ 的正方形网格图中，A、B、C为格点，则 $t a n ∠ A B C$ 的值为（）

A、 $\frac{1}{3}$ B、 $\frac{1}{5}$ C、 $\frac{1}{7}$ D、 $\frac{1}{13}$

查看试题解析
5. 对于以下四个命题：①若直角三角形的两条边长与3与4，则第三边的长是5；② ${(\sqrt{a})}^{2} = a$ ；③若点 $P (a ， b)$ 在第三象限，则点 $Q (- a ， - b)$ 在第一象限；④两边及其第三边上的中线对应相等的两个三角形全等，正确的说法是（）

A、只有①错误，其他正确 B、①②错误，③④正确 C、①④错误，②③正确 D、只有④错误，其他正确

查看试题解析
6. 下列几组数能作为直角三角形三边长的是（）

A、2，3，4 B、4，5，6 C、6，8，10 D、12，18，25

查看试题解析
7. $△ A B C$ 中， $∠ A$ ， $∠ B$ ， $∠ C$ 的对边分别为a，b，c，下列条件能判断 $△ A B C$ 是直角三角形的是（）

A、 $∠ A = ∠ B = ∠ C$ B、 $a = 6$ ， $b = 7$ ， $c = 8$ C、 $∠ A ： ∠ B ： ∠ C = 3 ： 4 ： 5$ D、 $a^{2} + b^{2} = c^{2}$

查看试题解析
8. △ABC的三边为a，b，c且（a＋b）（a﹣b）＝c² ，则该三角形是（）

A、锐角三角形 B、以c为斜边的直角三角形 C、以b为斜边的直角三角形 D、以a为斜边的直角三角形

查看试题解析
9. 现有一楼房发生火灾，消防队员决定用消防车上的云梯救人，如图（1）已知云梯最多只能伸长到15m，消防车高3m．救人时云梯伸长至最长，在完成从12m高处救人后，还要从15m高处救人，这时消防车要从原处再向着火的楼房靠近的距离 $A C$ 为（）

A、3米 B、5米 C、7米 D、9米

查看试题解析
10. 如图所示，圆锥的底面圆的半径为5，母线长为30，一只蜘蛛从底面圆周上一点A出发沿圆锥的侧面爬行一周后回到A点的最短路程是（　　）

A、8 B、 $10 \sqrt{2}$ C、30 D、 $20 \sqrt{2}$

查看试题解析

二、填空题

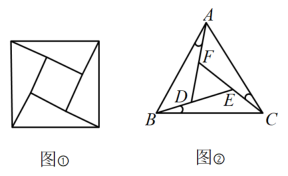
11. 《九章算术》中，赵爽利用“弦图”（如图①）证明了勾股定理，类比此方法研究等边三角形（如图②）：在等边三角形ABC中，如果∠BAD=∠CBE=∠ACF，那么△ABD的三边存在一定的数量关系，设BD=a，AD=b，AB=c，则这三边a，b，c满足的数量关系是．

查看试题解析
12. 如图，某港口P位于东西方向的海岸线上，“远航”号、“海天”号轮船同时离开港口，各自沿一固定方向航行，“远航”号每小时航行16nmile，“海天”号每小时航行12nmile，它们离开港口一个半小时后相距30nmile，且知道“远航”号沿东北方向航行，那么“海天”号航行的方向是.

查看试题解析
13. 如图，在Rt△ACB中，AC＝6、AB＝10，AD平分∠CAB，BD⊥AD，AD的值是．

查看试题解析
14. 如图，图①是棱长为4cm的立方体，沿其相邻三个面的对角线(虚线)裁掉一个角，得到如图②的几何体，则一只蚂蚁沿着图②几何体的表面，从顶点A爬到顶点B的最短距离为 cm.

查看试题解析
15. 如图，已知阴影部分是一个正方形， $A B = 4 ， ∠ B =$ $45^{°}$ ，则此正方形的面积为

查看试题解析

三、解答题

16. 如图，小刚想知道学校旗杆的高度，他发现旗杆顶端A处的绳子垂到地面B处后还多2米 $.$ 当他把绳子拉直并使下端刚好接触到地面C处，发现绳子下端到旗杆下端的距离为6米，请你帮小刚求出旗杆的高度AB长．

查看试题解析
17. 如图，已知扶梯AB的坡比为4： 3，滑梯CD的坡比为1 ： 2，AE=30 m，BC=30 m．问：一男孩从扶梯走到滑梯的顶部，然后从滑梯滑下，共经过了多少路程？

查看试题解析
18. 如图，长方体的长为 $15 c m$ ，宽为 $10 c m$ ，高为 $20 c m$ ，点 $B$ 到点 $C$ 的距离是 $5 c m$ ，在点 $B$ 处有一滴蜂蜜，一只蚂蚁如果沿着长方体的表面从点 $A$ 爬行到点 $B$ 去吃蜂蜜，蚂蚁需要爬行的最短路程是多少？请通过画图和计算进行解答.

查看试题解析
19. 已知，如图，等腰△ABC的底边BC＝10cm，D是腰AB上一点，且CD＝8cm，BD＝6cm，求AB的长.

查看试题解析
20. 如图，小明将升旗的绳子拉到旗杆底端，绳子末端刚好接触地面，然后将绳子末端拉到距离旗杆5m处，发现此时绳子末端距离地面1m，求旗杆的高度．（滑轮上方的部分忽略不计）

查看试题解析
21. 某小区有一块如图所示的四边形空地ABCD，为了庆祝建党百年，小区物业决定在这块空地上种植花草，测得已知 $A D = 8 m$ ， $C D = 6 m$ ， $∠ D = 90 °$ ， $A B = 26 m$ ， $B C = 24 m$ .种植花草的费用为80元 $/ m^{2}$ ，则该空地种植花草共需多少元？

查看试题解析
22. 《九章算术》是我国古代第一部数学专著，它的出现标志中国古代数学形成了完整的体系，“折竹抵地”问题源自《九章算术》中：“今有竹高一丈，去本四尺，问折者高几何？”翻译成数学问题是：如图所示，∠ACB＝90°，AC+AB＝10尺，BC=4尺，求AC的长．

查看试题解析
23. 如图，四边形 $A B C D$ 中， $A B = 20$ ， $B C = 15$ ， $C D = 7$ ， $A D = 24$ ， $∠ B = 90 °$ ，求证： $∠ D = 90 °$ ．

查看试题解析

（人教版）2021-2022学年度第二学期八年级数学第17章勾股定理 期末复习测试卷

一、单选题

二、填空题

三、解答题

（人教版）2021-2022学年度第二学期八年级数学第17章勾股定理期末复习测试卷