(人教版)2021-2022学年度第二学期八年级数学17.1勾股定理 期末复习测试卷
试卷更新日期:2022-05-27 类型:复习试卷
一、单选题
-
1. 如图,数轴上的点A 所表示的数为x,则x的值为( )
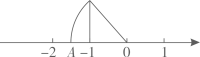 A、 B、
A、 B、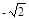 C、2
D、-2
2. 已知 中, , , ,则 的周长等于( )A、11 B、 C、12 D、133. 《九章算术》是我国古代最重要的数学著作之,在《勾股》章中记载了一道“折竹抵地”问题:“今有竹高一丈,末折抵地,去本三尺,间折者高几何?”翻译成数学问题;如图,在 中, , , ,若设 ,则可列方程为( )
C、2
D、-2
2. 已知 中, , , ,则 的周长等于( )A、11 B、 C、12 D、133. 《九章算术》是我国古代最重要的数学著作之,在《勾股》章中记载了一道“折竹抵地”问题:“今有竹高一丈,末折抵地,去本三尺,间折者高几何?”翻译成数学问题;如图,在 中, , , ,若设 ,则可列方程为( ) A、 B、 C、 D、4. 一个直角三角形的两直角边长分别为5和12,则斜边长为( )A、13 B、14 C、 D、155. 如图, ,垂足为D, , , ,则△BCE周长为( )
A、 B、 C、 D、4. 一个直角三角形的两直角边长分别为5和12,则斜边长为( )A、13 B、14 C、 D、155. 如图, ,垂足为D, , , ,则△BCE周长为( ) A、16 B、17 C、18 D、196. 如图,在平面直角坐标系中,点P坐标为(﹣2,3),以点O为圆心,以OP的长为半径画弧,交x轴的负半轴于点A,则点A的横坐标介于( )
A、16 B、17 C、18 D、196. 如图,在平面直角坐标系中,点P坐标为(﹣2,3),以点O为圆心,以OP的长为半径画弧,交x轴的负半轴于点A,则点A的横坐标介于( ) A、﹣4和﹣3之间 B、﹣5和﹣4之间 C、3和4之间 D、4和5之间7. 如图,所有阴影部分四边形都是正方形,所有三角形都是直角三角形,若正方形A、B、D的面积依次为6、10、24,则正方形C的面积为( )
A、﹣4和﹣3之间 B、﹣5和﹣4之间 C、3和4之间 D、4和5之间7. 如图,所有阴影部分四边形都是正方形,所有三角形都是直角三角形,若正方形A、B、D的面积依次为6、10、24,则正方形C的面积为( )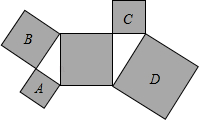 A、4 B、6 C、8 D、128. 如图,四个全等的直角三角形围成一个大正方形,中间空出的部分是一个小正方形,这样就组成了一个“赵爽弦图”.若直角三角形的两条直角边长分别为2和3,则大正方形与小正方形的面积之比为( )
A、4 B、6 C、8 D、128. 如图,四个全等的直角三角形围成一个大正方形,中间空出的部分是一个小正方形,这样就组成了一个“赵爽弦图”.若直角三角形的两条直角边长分别为2和3,则大正方形与小正方形的面积之比为( ) A、9:2 B、1:13 C、1:14 D、2:159. 雪上项目占据了2022年北京冬奥会的大部分比赛项目,有自由式滑雪、越野滑雪、跳台滑雪、无舵雪橇、有舵雪橇、高山滑雪等.如图,某滑雪运动员在坡度为5:12的雪道上下滑65m,则该滑雪运动员沿竖直方向下降的高度为( )
A、9:2 B、1:13 C、1:14 D、2:159. 雪上项目占据了2022年北京冬奥会的大部分比赛项目,有自由式滑雪、越野滑雪、跳台滑雪、无舵雪橇、有舵雪橇、高山滑雪等.如图,某滑雪运动员在坡度为5:12的雪道上下滑65m,则该滑雪运动员沿竖直方向下降的高度为( ) A、13m B、25m C、m D、156 m10. 如图,中, , , 的垂直平分线交于D,连接 , 若 , 则的长为( )
A、13m B、25m C、m D、156 m10. 如图,中, , , 的垂直平分线交于D,连接 , 若 , 则的长为( )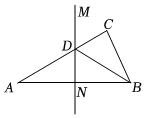 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 一架云梯长2.5米,如图斜靠在一面墙上,梯子的底端离墙0.7米,如果梯子的顶端下滑了0.4米,那么梯子的底端在水平方向滑动了米.
 12. 如图,在 中, ,若 ,则线段 的长为.
12. 如图,在 中, ,若 ,则线段 的长为. 13. 若一个直角三角形的一条直角边和斜边长分别为6,10,则第三边长为.14. 在△ABC中,AD为高, , , , 则 .15. 有一个水池,水面是一个边长为10尺的正方形,在水池正中央有一根芦苇,它高出水面1尺.如果把这根芦苇拉向水池一边的中点,它的顶端恰好到达池边的水面,这根芦苇的长度为尺.
13. 若一个直角三角形的一条直角边和斜边长分别为6,10,则第三边长为.14. 在△ABC中,AD为高, , , , 则 .15. 有一个水池,水面是一个边长为10尺的正方形,在水池正中央有一根芦苇,它高出水面1尺.如果把这根芦苇拉向水池一边的中点,它的顶端恰好到达池边的水面,这根芦苇的长度为尺.三、解答题
-
16. 如图,在△ABC中,∠C=90°,∠A=30°,点D在AC上,且∠BDC=60°,AC=12,求BD、BC的长.
 17. 如图,在一次课外活动中,同学们要测量某公园人工湖两侧A,B两个凉亭之间的距离,已知CD⊥BD,现测得AC= ,BC= ,CD= ,请计算A,B两个凉亭之间的距离.
17. 如图,在一次课外活动中,同学们要测量某公园人工湖两侧A,B两个凉亭之间的距离,已知CD⊥BD,现测得AC= ,BC= ,CD= ,请计算A,B两个凉亭之间的距离. 18. 如图,某海岸线MN的方向为北偏东75°,甲,乙两船分别向海岛C运送物资,甲船从港口A处沿北偏东45°方向航行,乙船从港口B处沿北偏东30°方向航行,已知港口B到海岛C的距离为30海里,求港口A到海岛C的距离.
18. 如图,某海岸线MN的方向为北偏东75°,甲,乙两船分别向海岛C运送物资,甲船从港口A处沿北偏东45°方向航行,乙船从港口B处沿北偏东30°方向航行,已知港口B到海岛C的距离为30海里,求港口A到海岛C的距离. 19. 在甲村至乙村的公路旁有一块山地正在开发,现有一C处需要爆破.已知点C与公路上的停靠站A的距离为500米,与公路上另一停靠站B的距离为1200米,且CA⊥CB,如图,为了安全起见,爆破点C周围半径400米范围内不得进入.问在进行爆破时,公路AB段是否有危险,是否需要暂时封锁?请通过计算进行说明.
19. 在甲村至乙村的公路旁有一块山地正在开发,现有一C处需要爆破.已知点C与公路上的停靠站A的距离为500米,与公路上另一停靠站B的距离为1200米,且CA⊥CB,如图,为了安全起见,爆破点C周围半径400米范围内不得进入.问在进行爆破时,公路AB段是否有危险,是否需要暂时封锁?请通过计算进行说明. 20. 如图,铁路上A,B两点相距25km,C,D为两村庄,于点A,于点B,若 , , 现要在AB上建一个周转站E,使得C,D两村到E站的距离相等,则周转站E应建在距A点多远处?
20. 如图,铁路上A,B两点相距25km,C,D为两村庄,于点A,于点B,若 , , 现要在AB上建一个周转站E,使得C,D两村到E站的距离相等,则周转站E应建在距A点多远处?


