浙江省温州市瓯海区2022年初中毕业生学业考试第二次适应性测试数学试卷
试卷更新日期:2022-05-27 类型:中考模拟
一、选择题(本题有10小题,每小题4 分,共40分请选出各题中唯一的正确选项,不选、多选、错选,均不给分)
-
1. 在数-3,-2,0,3中,最小的数是( )A、-3 B、-2 C、0 D、32. 根据调查显示,温州市去年中考报名人数约87300人,87300 用科学记数法可以表示为( )A、873×102 B、87.3×103 C、8.73×104 D、0.873×1043. 如图,是由三个相同的小立方体组成的几何体,该几何体的左视图是( )
 A、
A、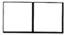 B、
B、 C、
C、 D、
D、 4. 一个不透明的袋中,装有2个黄球,3个红球和5个白球,它们除颜色外都相同.从袋中任意摸出一个球,是黄球的概率是( )A、 B、 C、 D、5. 如图为小王同学周末复习各学科投入时间扇形统计图,其中在语文学科投入时间为1小时,则她在数学学科投入时间为( )
4. 一个不透明的袋中,装有2个黄球,3个红球和5个白球,它们除颜色外都相同.从袋中任意摸出一个球,是黄球的概率是( )A、 B、 C、 D、5. 如图为小王同学周末复习各学科投入时间扇形统计图,其中在语文学科投入时间为1小时,则她在数学学科投入时间为( )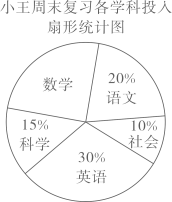 A、0.5小时 B、1小时 C、1.25小时 D、1.5小时6. 函数y= 中自变量x的取值范围是( )A、x≥0 B、x≥-1 C、x>-1 D、任意实数7. 如图是小明在解方程 x2-2x-1= 0时的过程,他在解答过程中开始出错的步骤是( )
A、0.5小时 B、1小时 C、1.25小时 D、1.5小时6. 函数y= 中自变量x的取值范围是( )A、x≥0 B、x≥-1 C、x>-1 D、任意实数7. 如图是小明在解方程 x2-2x-1= 0时的过程,他在解答过程中开始出错的步骤是( ) A、第①步 B、第②步 C、第③步 D、第④步8. 如图为一节楼梯的示意图,BC⊥AC,∠BAC=α,AC=6米,现要在楼梯上铺一块地毯, 楼梯宽度AD为1米,则地毯的面积至少需要( )平方米.
A、第①步 B、第②步 C、第③步 D、第④步8. 如图为一节楼梯的示意图,BC⊥AC,∠BAC=α,AC=6米,现要在楼梯上铺一块地毯, 楼梯宽度AD为1米,则地毯的面积至少需要( )平方米.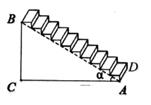 A、6tanα+ 6 B、 C、 D、9. 已知y=ax2+bx+3(a≠0)的对称轴为直线x=2,与x轴的其中一个交点为(1,0),该函数在1≤x≤4的取值范围,下列说法正确的是( ).A、有最小值0,有最大值3 B、有最小值-1,有最大值3 C、有最小值-3,有最大值4 D、有最小值-1,有最大值410. 如图来自清朝数学家梅文鼎的《勾股举隅》,该图由四个全等的直角三角形围成,延长BC分别交AG,HG于点M,N,梅文鼎就是利用这幅图证明了勾股定理.若图中记△MNG的面积为S,△GDF的面积为9S,则阴影部分的面积为( )
A、6tanα+ 6 B、 C、 D、9. 已知y=ax2+bx+3(a≠0)的对称轴为直线x=2,与x轴的其中一个交点为(1,0),该函数在1≤x≤4的取值范围,下列说法正确的是( ).A、有最小值0,有最大值3 B、有最小值-1,有最大值3 C、有最小值-3,有最大值4 D、有最小值-1,有最大值410. 如图来自清朝数学家梅文鼎的《勾股举隅》,该图由四个全等的直角三角形围成,延长BC分别交AG,HG于点M,N,梅文鼎就是利用这幅图证明了勾股定理.若图中记△MNG的面积为S,△GDF的面积为9S,则阴影部分的面积为( )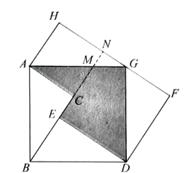 A、20S B、21S C、22S D、24S
A、20S B、21S C、22S D、24S二、填空题(本题有6小题,每小题5分,共30分)
-
11. 因式分解:2m2-18=12. 甲、乙、丙、丁四位同学五次数学测验成绩的平均数和方差统计如下表,如果从这四位同学中,选出一位成绩较好且状态稳定的同学参加初中数学竞赛,那么应选 同学.
甲
乙
丙
丁
平均分(分)
78
92
92
85
方差(分2)
7.5
6
7
6
13. 圆锥的底面半径长为6,母线长为10,则圆锥的侧面积为14. 直线y=-2x+3与x轴, y轴分别交于点A,B,将这条直线向左平移与x轴,y轴分别交于点C,D.若AB=AD,则点C的坐标是15. 如图,在平面直角坐标系中,△ABC为等腰直角三角形,∠ABC=90°,AC∥x轴,经过点B的反比例函数y= (k>0)交AC于点D,过点D作DE⊥x轴于点E,若AD=3CD,DE=6,则k=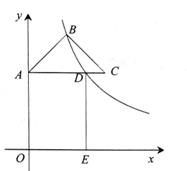 16. 如图2是一盏路灯的侧面示意图,OA为灯杆,点B是灯所在位置,DE为路灯在地面的照射范围,∠DBE=∠A,光线BE交OA于点C,测量得OC= 米,AC=AB= 米,灯杆OC在地面的影子OE= 米,点B到地面的高度BF为米,DE=米.
16. 如图2是一盏路灯的侧面示意图,OA为灯杆,点B是灯所在位置,DE为路灯在地面的照射范围,∠DBE=∠A,光线BE交OA于点C,测量得OC= 米,AC=AB= 米,灯杆OC在地面的影子OE= 米,点B到地面的高度BF为米,DE=米.
三、解答题(本题有8小题,共80分.解答需写出必要的文字说明、演算步骤或证明过程)
-
17.(1)、计算: |-2|-4cos60°+(-1)0 .(2)、化简:(x+2)2-x(x-2).18. 如图,AB,DE交于点F,AD∥BE,点C在线段AB上,且AC=BE,AD=BC,连结CD,CE.
 (1)、求证:△ADC≌△BCE.(2)、若∠A=40°,∠ADC=20°,求∠CDE的度数.19. 如图,在方格纸中,点A,B,P都在格点上.请按要求画出以AB为边的格点图形(图形的每个端点都在格点上).
(1)、求证:△ADC≌△BCE.(2)、若∠A=40°,∠ADC=20°,求∠CDE的度数.19. 如图,在方格纸中,点A,B,P都在格点上.请按要求画出以AB为边的格点图形(图形的每个端点都在格点上).
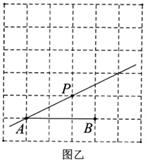 (1)、在图甲中画出一个三角形ABC,使直线BP平分该三角形的面积.(2)、在图乙中画出一个至少有一组对边平行的四边形ABMN,使直线AP平分该四边形的面积.20. 某公司销售部有营销人员15人,为了对达到或者超出月销售定额的员工进行表彰,统计了这15人某月的销售量(单位:件)如下:
(1)、在图甲中画出一个三角形ABC,使直线BP平分该三角形的面积.(2)、在图乙中画出一个至少有一组对边平行的四边形ABMN,使直线AP平分该四边形的面积.20. 某公司销售部有营销人员15人,为了对达到或者超出月销售定额的员工进行表彰,统计了这15人某月的销售量(单位:件)如下:每人销售件数
1400
880
270
150
130
120
人数
1
1
3
6
3
11
(1)、求这15位营销人员该月销售量的平均数;(2)、为了激励员工产生工作动力,销售负责人把月销售定额定为280件,你认为是否合理,为什么?如不合理,请你制定一个较合理的销售定额,并说明理由.21. 已知抛物线y=ax2+bx-2经过点(2,-2),(4,6) .(1)、求抛物线的函数表达式.(2)、已知点D(m,y1),E(n,y1),y1>-2,D,E是抛物线上不同的两点,其中点D在点E左侧.若点C(2,y1)在线段DE上,且m+n=4CE,求点D的坐标.22. 如图,在Rt△ABC中,∠BAC=90°,以AB为一边构造 ABDE,DA∥BC,连结EC交DA的延长线于点F,DF⊥EC,延长EA交BC于点G. (1)、求证:点A是EG的中点(2)、若tan∠ABC= ,DA=6,求BC的长.23. 某早餐店推出如图所示的套餐一促销活动,某天小明到店买早餐,与店员产生如下对话.
(1)、求证:点A是EG的中点(2)、若tan∠ABC= ,DA=6,求BC的长.23. 某早餐店推出如图所示的套餐一促销活动,某天小明到店买早餐,与店员产生如下对话.
小明:你好,我要2个A款三明治和1个B款三明治.
店员:需要饮料吗?要不要加12元换成3份三明治套餐一?
小明:这样太多了,A款、B款三明治各1个,再来个套餐一好了。
店员:好的,一共24元.
(1)、请根据信息求出A,B两款三明治的单价.(2)、若小华计划购买50个三明治,其中A款三明治不多于B款的两倍,则小华至少花费多少元才能购买这些三明治.(3)、已知指定饮品的单价为5元,除了套餐一活动外,店内还推出套餐二活动:任意购买三个三明治加一杯指定饮品共21元.某公司打算为员工购买200个三明治和100瓶指定饮品,请你在表格中设计一种购买方案,使总花费少于1570元.套餐购买数量
单独购买数量
套餐一
套餐二
三明治
指定饮品
份
份
个
个
24. 如图,四边形ABCD为⊙O的内接四边形,延长BA,CD交于点E,连结AC,BD,AC⊥BD于点F,连结BO并延长交CD于点G,BG交AC于点H,已知∠BAC=∠EAD,BC= ,CD= (1)、求证:BG⊥CD(2)、求cos∠ABD的值与AB的长.(3)、连结OD,若P是线段AC上一点,当点P关于△OBD一边所在直线的对称点落在边BE或BC上时,求出所有满足条件的AP的长.
(1)、求证:BG⊥CD(2)、求cos∠ABD的值与AB的长.(3)、连结OD,若P是线段AC上一点,当点P关于△OBD一边所在直线的对称点落在边BE或BC上时,求出所有满足条件的AP的长.