天津市十二区县重点学校2022届高三下学期数学毕业班联考试卷（一）

试卷更新日期：2022-05-27 类型：高考模拟

进入出卷网下载

一、单选题

1. 设全集 $U = {x \in Z | - 3 < x < 4}$ ，集合 $A = {- 2 ， 0 ， 1 ， 2}$ ， $B = {- 1 ， 0 ， 1}$ ，则 $A ∩ (∁_{U} B) =$ （）

A、 ${- 2 ， 2}$ B、 ${- 1 ， 3}$ C、 ${- 2 ， 2 ， 3}$ D、{-1}

查看试题解析
2. 在等比数列 ${a_{n}}$ 中，公比是 $q$ ，则“ $q > 1$ ”是“ $a_{n + 1} > a_{n} (n \in N^{*})$ ”的（）

A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件

查看试题解析
3. 函数 $f (x) = \frac{x - \sin x}{x^{2} + 1}$ 的图象大致为（）

A、 B、 C、 D、

查看试题解析
4. 下列说法正确的是（）

A、若随机变量 $X ~ N (1 ， σ^{2})$ ， $P (X > 2) = 0.2$ ，则 $P (0 < X < 1) = 0.2$ B、数据7，4，2，9，1，5，8，6的第50百分位数为5 C、将一组数据中的每一个数据加上同一个常数后，方差不变 D、设具有线性相关关系的两个变量x，y的相关系数为r，则 $| r |$ 越接近于0，x和y之间的线性相关程度越强

查看试题解析
5. 已知幂函数 $f (x)$ 的图象经过点 $A (3 ， 27)$ 与点 $B (t ， 64)$ ， $a = l o g_{0.1} t$ ， $b = 0 . 2^{t}$ ， $c = t^{0.1}$ ，则（）

A、 $c < a < b$ B、 $a < b < c$ C、 $b < a < c$ D、 $c < b < a$

查看试题解析
6. 设抛物线 $C_{1}$ ： $y = \frac{1}{8} x^{2}$ 与双曲线 $C_{2}$ ： $\frac{y^{2}}{a^{2}} - \frac{x^{2}}{b^{2}} = 1 (a > 0 ， b > 0)$ 有公共的焦点F，直线l为过双曲线另外的一个焦点且与其渐近线平行的直线，F到直线l距离为 $2 \sqrt{3}$ ，则双曲线 $C_{2}$ 的离心率为（）

A、2 B、 $\sqrt{3}$ C、 $\sqrt{5}$ D、 $\frac{2 \sqrt{7}}{7}$

查看试题解析
7. 已知函数 $f (x) = c o s^{4} x - 2 s i n x c o s x - s i n^{4} x$ .给出下列结论：.
① $f (x)$ 的最小正周期为 $π$ ；② $f (x)$ 在区间 $[- \frac{π}{4} ， \frac{π}{4}]$ 上是增函数；③ $f (x)$ 的图象关于直线 $x = \frac{5 π}{8}$ 对称；④把函数 $y = \sqrt{2} s i n 2 x$ 的图象上所有点向左平移 $\frac{3 π}{8}$ 个单位长度，可得到函数 $y = f (x)$ 的图象.
其中正确结论的个数是（）

A、1 B、2 C、3 D、4

查看试题解析
8. 已知函数 $f (x) = - s i n x - 2 | s i n x |$ ，关于x的方程 $f^{2} (x) + \sqrt{a} f (x) - 1 = 0$ 有以下结论
①当 $a \geq 0$ 时，方程 $f^{2} (x) + \sqrt{a} f (x) - 1 = 0$ 在 $[0 ， 2 π]$ 最多有3个不等实根；②当 $0 \leq a < 3$ 时，方程 $f^{2} (x) + \sqrt{a} f (x) - 1 = 0$ 在 $[0 ， 2 π]$ 内有两个不等实根；③若方程 $f^{2} (x) + \sqrt{a} f (x) - 1 = 0$ 在 $[0 ， 6 π]$ 内根的个数为偶数，则所有根之和为 $15 π$ ；④若方程 $f^{2} (x) + \sqrt{a} f (x) - 1 = 0$ 在 $[0 ， 6 π]$ 内根的个数为偶数，则所有根之和为 $36 π$ .

其中所有正确结论的序号是（）

A、①③ B、②④ C、①④ D、①②③

查看试题解析

二、解答题

9. 已知一个正三棱柱所有棱长均为3，若该正三棱柱内接于半球体，即正三棱柱的上底面的三个顶点在球面上，下底面的三个顶点在半球体的底面圆内，则该半球体的体积为（）

A、 $32 \sqrt{3} π$ B、 $16 \sqrt{3} π$ C、 $48 π$ D、 $24 π$

查看试题解析
10. 在 $△ A B C$ 中，角 $A$ ， $B$ ， $C$ 所对的边分别为a，b，c，已知 $b = a c o s C + \frac{\sqrt{3}}{3} c s i n A$ .

(1)、求角A的大小：.

(2)、若 $a = \sqrt{7}$ ， $b < c$ ， $△ A B C$ 的面积为 $\frac{3 \sqrt{3}}{2}$ .
①求b，c的长；
②求 $s i n (2 B - \frac{π}{6})$ 的值.

查看试题解析
11. 如图，在四棱锥P-ABCD中，底面ABCD是直角梯形， $∠ A B C = ∠ B A D = 90 °$ ， AP⊥平面ABCD， $A B = B C = 2 A P = 2 A D = 2$ ，点M、N分别为线段BC和PD的中点．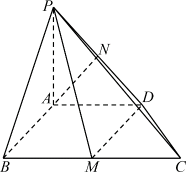

(1)、求证：AN⊥平面PDM；

(2)、求平面PDM与平面PDC夹角的正弦值；

(3)、在线段PC(不包括端点)上是否存在一点E，使得直线BE与平面PDC所成角的正弦值为 $\frac{2}{3}$ ，若存在，求出线身PE的长：若不存在，请说明理由.

查看试题解析
12. 已知椭圆 $C ： \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ ，其离心率为 $\frac{1}{2}$ ，右焦点为 $F$ ，两焦点与短轴两端点围成的四边形面积为 $2 \sqrt{3}$ .

(1)、求椭圆 $C$ 的标准方程：

(2)、直线 $l$ 与椭圆有唯一的公共点 $M$ （ $M$ 在第一象限，此直线 $l$ 与 $y$ 轴的正半轴交于点 $N$ ，直线 $N F$ 与直线 $O M$ 交于点 $P$ 且 $S_{△ O F P} = \frac{3}{7} S_{△ O F N}$ ，求直线 $l$ 的斜率.

查看试题解析
13. 已知数列 ${a_{n}}$ 是等差数列，其前n项和为 $A_{n}$ ， $a_{7} = 15$ ， $A_{7} = 63$ ；数列 ${b_{n}}$ 的前n项和为 $B_{n}$ ， $2 B_{n} = 3 b_{n} - 3 (n \in N^{*})$ .

(1)、求数列 ${a_{n}}$ ， ${b_{n}}$ 的通项公式；

(2)、求数列 ${\frac{1}{A_{n}}}$ 的前n项和 $S_{n}$ ；

(3)、求证： $\sum_{k = 1}^{n} \frac{a_{k}}{B_{k}} < 2$ .

查看试题解析
14. 已知函数 $f (x) = 2 l n x - a x^{2} + 2 x - 1 ，$ $g (x) = f (x) - 2 a x + 3 (a \in R)$ .

(1)、若 $f (1) = - 1$ ，求函数 $y = f (x)$ 的单调增区间；

(2)、若关于x的不等式 $g (x) \leq 0$ 恒成立，求整数a的最小值；

(3)、当 $0 < a < 1$ 时，函数 $g (x)$ 恰有两个不同的零点 $x_{1} ， x_{2}$ ，且 $x_{1} < x_{2}$ ，求证： $x_{1} + \frac{4}{3} x_{2} > \frac{7}{3 a}$ .

查看试题解析

三、填空题

15. i是虚数单位，则 $| \frac{2 + i}{4 - 3 i} |$ 的值为.

查看试题解析
16. 在二项式 ${(\frac{a}{x} - \sqrt[3]{x})}^{5}$ 的展开式中，各项系数的和为 $32$ ，则展开式中 $\frac{1}{x}$ 的系数是.（用数字作答）

查看试题解析
17. 直线l： $x - y - m = 0$ 被圆C： $x^{2} + y^{2} - 4 x + 6 y - 3 = 0$ 截得的弦长为 $4 \sqrt{2}$ ，则m的值为.

查看试题解析
18. 已知正实数 $a ， b$ ，满足 $3 a + b = 2$ ，则 $(a + \frac{1}{a}) (b + \frac{9}{b})$ 的最小值为.

查看试题解析
19. 投壶是从先秦延续至清末的汉民族传统礼仪和宴饮游戏，在春秋战国时期较为盛行，假设甲､乙是唐朝的两位投壶游成参与者，且甲､乙每次投壶投中的概率分别为 $\frac{1}{2}$ ､ $\frac{1}{3}$ 若每人均投一次，则仅有一人投中的概率为；若每人均投壶3次，则甲比乙多投中2次的概率为.

查看试题解析
20. 在△ABC中， $A B = A C = 3$ ， $\vec{A D} = 4 \vec{B D}$ ， $2 \vec{C E} = \vec{D A}$ ， $\vec{A E} \cdot \vec{C D} = - 8$ ，则 $c o s ∠ B A C =$ ，若动点F在线段AC上，则 $\vec{D F} \cdot \vec{E F}$ 的最小值为.

查看试题解析