四川省南充市2022届高三下学期理数高考适应性考试(三诊)试卷
试卷更新日期:2022-05-27 类型:高考模拟
一、单选题
-
1. 已知集合 , 则=( )A、[-1,0) B、[-1,0] C、(-1,0) D、(-1,0]2. 设 , 则“方程表示双曲线”的必要不充分条件为( )A、 B、 C、 D、3. 为考查A,B两种药物预防某疾病的效果,进行动物实验,分别得到如下等高条形图:根据图中信息,在下列各项中,说法最佳的一项是( )
 A、药物B的预防效果优于药物A的预防效果 B、药物A的预防效果优于药物B的预防效果 C、药物A,B对该疾病均有显著的预防效果 D、药物A,B对该疾病均没有预防效果4. 已知随机变量 , 且 , 则的展开式中常数项为( )A、-240 B、-60 C、240 D、605. 以坐标原点O为圆心的圆全部都在平面区域内,则圆O的面积的最大值为( )A、 B、 C、2π D、π6. 函数的图象可能是( )A、
A、药物B的预防效果优于药物A的预防效果 B、药物A的预防效果优于药物B的预防效果 C、药物A,B对该疾病均有显著的预防效果 D、药物A,B对该疾病均没有预防效果4. 已知随机变量 , 且 , 则的展开式中常数项为( )A、-240 B、-60 C、240 D、605. 以坐标原点O为圆心的圆全部都在平面区域内,则圆O的面积的最大值为( )A、 B、 C、2π D、π6. 函数的图象可能是( )A、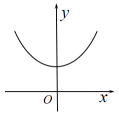 B、
B、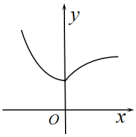 C、
C、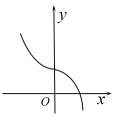 D、
D、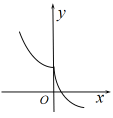 7. 已知等差数列的公差为d,有下列四个等式:①②③④;若其中只有一个等式不成立,则不成立的是( )A、① B、② C、③ D、④8. 在中, , , , , , CN与BM交于点P,则的值为( )A、 B、 C、 D、9. 教室通风的目的是通过空气的流动,排出室内的污浊空气和致病微生物,降低室内二氧化碳和致病微生物的浓度,送进室外的新鲜空气.按照国家标准,教室内空气中二氧化碳日平均最高容许浓度应小于0.15%.经测定,刚下课时,空气中含有0.25%的二氧化碳,若开窗通风后教室内二氧化碳的浓度为y%,且随时间(单位:分钟)的变化规律可以用函数描述,则该教室内的二氧化碳浓度达到国家标准需要的时间(单位:分钟)的最小整数值为( )(参考数据 , )A、7 B、9 C、10 D、1110. 设 , , , 则a,b,c的大小关系为( )A、 B、 C、 D、11. 已知P为椭圆上任意一点,点M,N分别在直线与上,且 , , 若为定值,则椭圆的离心率为( )A、 B、 C、 D、12. 已知函数 , 过点作函数图象的两条切线,切点分别为M,N.则下列说法正确的是( )A、 B、直线MN的方程为 C、 D、的面积为
7. 已知等差数列的公差为d,有下列四个等式:①②③④;若其中只有一个等式不成立,则不成立的是( )A、① B、② C、③ D、④8. 在中, , , , , , CN与BM交于点P,则的值为( )A、 B、 C、 D、9. 教室通风的目的是通过空气的流动,排出室内的污浊空气和致病微生物,降低室内二氧化碳和致病微生物的浓度,送进室外的新鲜空气.按照国家标准,教室内空气中二氧化碳日平均最高容许浓度应小于0.15%.经测定,刚下课时,空气中含有0.25%的二氧化碳,若开窗通风后教室内二氧化碳的浓度为y%,且随时间(单位:分钟)的变化规律可以用函数描述,则该教室内的二氧化碳浓度达到国家标准需要的时间(单位:分钟)的最小整数值为( )(参考数据 , )A、7 B、9 C、10 D、1110. 设 , , , 则a,b,c的大小关系为( )A、 B、 C、 D、11. 已知P为椭圆上任意一点,点M,N分别在直线与上,且 , , 若为定值,则椭圆的离心率为( )A、 B、 C、 D、12. 已知函数 , 过点作函数图象的两条切线,切点分别为M,N.则下列说法正确的是( )A、 B、直线MN的方程为 C、 D、的面积为二、填空题
-
13. 若复数 , 则z在复平面内对应的点在第象限.14. 若等比数列 的前 项和为 ,且 , ,则 .15. 正方形ABCD边长为3,P为正方形ABCD边界及内部的动点,且 , 则动点P的轨迹长度为 .16. 如图,在三棱锥中,三条侧棱OA,OB,OC两两垂直,且 , M为内部一动点,过M分别作平面OAB,平面OBC,平面OAC的垂线,垂足分别为P,Q,R.

①直线PR与直线BC是异面直线;
②为定值;
③三棱锥的外接球表面积的最小值为;
④当时,平面PQR与平面OBC所成的锐二面角为45°.
则以上结论中所有正确结论的序号是 .
三、解答题
-
17. 已知的三个内角A,B,C所对的边分别为a,b,c,且 , , .(1)、求的值;(2)、求的值.18. 2022年春节后,新冠肺炎的新变种奥密克戎在我国部分地区爆发.该病毒是一种人传人,不易被人们直接发现,潜伏期长且传染性极强的病毒.我们把与该病毒感染者有过密切接触的人群称为密切接触者.一旦发现感染者,社区会立即对其进行流行性病医学调查,找到其密切接触者进行隔离观察.调查发现某位感染者共有10位密切接触者,将这10位密切接触者隔离之后立即进行核酸检测.核酸检测方式既可以采用单样本检测,又可以采用“k合1检测法”.“k合1检测法”是将k个样本混合在一起检测,若混合样本只要呈阳性,则该组中各个样本再全部进行单样本检测;若混合样本呈阴性,则可认为该混合样本中每个样本都是阴性.通过病毒指标检测,每位密切按触者为阴性的概率为 , 且每位密切接触者病毒指标是否为阴性相互独立.(1)、现对10个样本进行单样本检测,求检测结果最多有2个样本为阳性的概率的表达式;(2)、若对10个样本采用“5合1检测法”进行核酸检测.
①求某个混合样本呈阳性的概率;
②设总检测次数为X,求X的分布列和数学期望 .
19. 下图甲是由直角梯形ABCD和等边三角形CDE组成的一个平面图形,其中 , , , 将沿CD折起使点E到达点P的位置(如图乙),使二面角为直二面角. (1)、证明:;(2)、若平面PCD与平面PAB的交线为l,求l与平面PAD所成角的正弦值.20. 已知点F是抛物线的焦点,直线l与抛物线C相切于点 , 连接PF交抛物线于另一点A,过点P作l的垂线交抛物线于另一点B.(1)、若 , 求直线l的方程;(2)、求三角形PAB面积S的最小值.21. 已知函数 .(1)、讨论的单调性;(2)、当时, , 若 , 求证:对于任意 , 函数有唯一零点.
(1)、证明:;(2)、若平面PCD与平面PAB的交线为l,求l与平面PAD所成角的正弦值.20. 已知点F是抛物线的焦点,直线l与抛物线C相切于点 , 连接PF交抛物线于另一点A,过点P作l的垂线交抛物线于另一点B.(1)、若 , 求直线l的方程;(2)、求三角形PAB面积S的最小值.21. 已知函数 .(1)、讨论的单调性;(2)、当时, , 若 , 求证:对于任意 , 函数有唯一零点.
