陕西省西安市周至县2022届高三下学期理数三模试卷

试卷更新日期：2022-05-27 类型：高考模拟

进入出卷网下载

一、单选题

1. 设集合 $A = {x | x \geq 1}$ ， $B = {x | - 1 < x < 5}$ ，则 $A ∩ B =$ （）

A、 $[1 ， 5)$ B、 $(- 1 ， 1]$ C、 $(1 ， 5)$ D、 $(- 1 ， 1)$

查看试题解析
2. 已知复数 $z$ 满足 $z (1 - i) = 2 i$ ，则 $| z + i | =$ （）

A、 $\sqrt{2}$ B、 $\sqrt{5}$ C、 $\sqrt{10}$ D、 $\sqrt{13}$

查看试题解析
3. 已知向量 $\vec{A B} = (4 ， - 4)$ ， $\vec{B C} = (- 3 ， m)$ ， $\vec{A D} = (- 1 ， m)$ ，若 $A$ ， $C$ ， $D$ 三点共线，则 $m =$ （）

A、2 B、 $\frac{2}{3}$ C、 $- 2 - \sqrt{6}$ D、 $- 2 + \sqrt{6}$

查看试题解析
4. 函数 $f (x) = x l n | x |$ 的图象大致是（）

A、 B、 C、 D、

查看试题解析
5. 从一批零件中抽取80个，测量其直径（单位： $mm$ ），将所得数据分为9组： $[5.31 ， 5.33) ， [5.33 ， 5.35) ， \dots ， [5.45 ， 5.47] ， [5.47 ， 5.49]$ ，并整理得到如下频率分布直方图，则在被抽取的零件中，直径落在区间 $[5.43 ， 5.47)$ 内的个数为（）

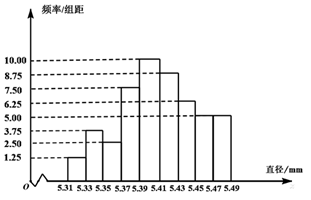
A、10 B、18 C、20 D、36

查看试题解析
6. 一个直角三角形的两条直角边长分别为2和 $2 \sqrt{3}$ ，将该三角形的斜边旋转一周得到的几何体的表面积为（）

A、 $(6 + 2 \sqrt{3}) π$ B、 $(6 - 2 \sqrt{3}) π$ C、 $2 \sqrt{3} π$ D、 $6 π$

查看试题解析
7. 设函数 $f (x) = a c o s x + b s i n x$ （a，b为常数），则“ $a b = 0$ ”是“ $f (x)$ 为偶函数”的（）

A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件

查看试题解析
8. 已知抛物线 $x^{2} = 2 p y (p > 0)$ 上一点 $A (x_{0} ， 3)$ ， $F$ 为其焦点，直线 $A F$ 交抛物线的准线于点 $B$ .且线段 $A B$ 的中点为 $F$ ，则 $x_{0} =$ （）

A、±3 B、 $\pm 2 \sqrt{2}$ C、 $\pm 3 \sqrt{3}$ D、 $\pm 2 \sqrt{3}$

查看试题解析
9. 在 ${(\frac{2}{x} - x)}^{6}$ 展开式中，下列说法错误的是（）

A、常数项为-160 B、第5项的系数最大 C、第4项的二项式系数最大 D、所有项的系数和为1

查看试题解析
10. 2022年4月16日，神舟十二号3名航天员告别了工作生活183天的中国空间站，安全返回地球中国征服太空的关键是火箭技术，在理想情况下，火箭在发动机工作期间获得速度增量的公式 $Δ v = v_{e} l n \frac{m_{0}}{m_{1}}$ ，其中△v为火箭的速度增量， $v_{e}$ 为喷流相对于火箭的速度， $m_{0}$ 和 $m_{1}$ 分别代表发动机开启和关闭时火箭的质量，在未来，假设人类设计的某火箭 $v_{e}$ 达到5公里/秒 $\frac{m_{0}}{m_{1}}$ ，从100提高到600，则速度增量 $△ v$ 增加的百分比约为（）（参考数据： $l n 2 \approx 0.7$ ， $l n 3 \approx 1.1$ ， $l n 5 \approx 1.6$

A、15% B、30% C、35% D、39%

查看试题解析
11. “中国剩余定理”又称“孙子定理”，可见于中国南北朝时期的数学著作《孙子算经》卷下中的“物不知数”问题，原文如下：今有物不知其数，三三数之剩二，五五数之剩三，七七数之剩二问物几何？现有一个相关的问题：将1到2022这2022个自然数中被3除余2且被5除余4的数按照从小到大的顺序排成一列，构成一个数列14，29，44，…，则该数列的项数为（）

A、132 B、133 C、134 D、135

查看试题解析
12. 若对任意的 $x_{1} ， x_{2} \in (m ， + \infty)$ ，且 $x_{1} < x_{2}$ ，都有 $\frac{x_{1} l n x_{2} - x_{2} l n x_{1}}{x_{2} - x_{1}} < 2$ 成立，则实数m的最小值是（）

A、1 B、 $e$ C、 $e^{- 2}$ D、 $e^{- 1}$

查看试题解析

二、填空题

13. 在等差数列 ${a_{n}}$ 中， $a_{3} + a_{6} + a_{9} = 39$ ，设数列 ${a_{n}}$ 的前 $n$ 项和为 $S_{n}$ ，则 $S_{11} =$ .

查看试题解析
14. 双曲线 $\frac{x^{2}}{m} - \frac{y^{2}}{12 - m} = 1 (0 < m < 12)$ 渐近线的斜率为k，且 $k^{2} > 2$ ，则m的取值范围是.

查看试题解析
15. 若函数 $y = s i n (2 ω x + \frac{π}{3})$ 的图像向右平移 $\frac{π}{6}$ 个单位长度后与函数 $y = c o s (2 ω x + \frac{π}{4})$ 的图象重合，则 $ω$ 的一个可能的值为；

查看试题解析
16. 如图，在正方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 中，点F是棱 $A A_{1}$ 上的一个动点，平面 $B F D_{1}$ 交棱 $C C_{1}$ 于点E，则下列正确说法的序号是.
①存在点F使得 $A_{1} C_{1} ∥$ 平面 $B E D_{1} F$ ；
②存在点F使得 $B_{1} D ∥$ 平面 $B E D_{1} F$ ；
③对于任意的点F，都有 $E F ⊥ B D$ ；
④对于任意的点F三棱锥 $E - F D D_{1}$ 的体积均不变.

查看试题解析

三、解答题

17. 在△ABC中，a，b，c分别为内角A，B，C的对边， $2 c c o s B + \sqrt{3} b = 3 a$ .

(1)、求C；

(2)、若 $c = 2$ ，求△ABC面积的最大值

查看试题解析
18. 在学校大课间体育活动中，甲､乙两位同学进行定点投篮比赛，每局比赛甲､乙每人各投第一次，若一方命中且另一方未命中，则命中的一方本局比赛获胜，否则为平局，已知甲､乙每次投篮命中的概率分别为 $\frac{4}{5}$ 和 $\frac{3}{4}$ ，且每局比赛甲､乙命中与否互不影响，各局比赛也互不影响.

(1)、求1局投篮比赛，甲､乙平局的概率；

(2)、求1局投篮比赛，甲获胜的概率；

(3)、设共进行了10局投篮比赛，其中甲获胜的局数为X，求X的数学期望 $E (X)$ .

查看试题解析
19. 如图①，在梯形ABCD中 $A D = 4$ ，四边形ABCE是边长为2的正方形，O是AC与BE的交点将△ABE沿BE折起到△PBE的位置，使得平面PBE⊥平面BCDE，如图②.

(1)、求证：OC⊥平面PBE；

(2)、求直线PB与平面PCD所成角的正弦值.

查看试题解析
20. 已知椭圆 $C$ ： $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ 的离心率为 $\frac{\sqrt{3}}{2}$ ，且短轴长等于双曲线： $x^{2} - \frac{y^{2}}{3} = 1$ 的实轴长.

(1)、求椭圆 $C$ 的标准方程；

(2)、若 $A$ ， $B$ 为椭圆 $C$ 上关于原点 $O$ 对称的两点，在圆 $D$ ： $x^{2} + y^{2} = 8$ 上存在点 $P$ ，使得 $△ P A B$ 为等边三角形，求直线 $A B$ 的方程.

查看试题解析
21. 已知函数 $f (x) = \frac{2 e x}{e^{x}}$ ， $g (x) = - x^{2} + 2 x + 1$ .

(1)、求函数 $f (x)$ 的单调区间和最值；

(2)、求证：当 $x < 1$ 时 $f (x) < g (x)$ ；当 $x > 1$ 时， $f (x) > g (x)$ ；

(3)、若存在 $x_{1} < x_{2}$ ，使得 $f (x_{1}) = f (x_{2})$ ，证明 $x_{1} + x_{2} > 2$ .

查看试题解析
22. 在直角坐标系 $x O y$ 中，直线 $l$ 的参数方程为： ${\begin{array}{l} x = 1 - t ， \\ y = 1 + t \end{array}$ （ $t$ 为参数）.在以 $O$ 为极点， $x$ 轴正半轴为极轴的极坐标系中，曲线 $C$ 的极坐标方程为： $ρ = 2 c o s θ$ .

(1)、求直线 $l$ 的普通方程和曲线 $C$ 的直角坐标方程；

(2)、若直线 $l$ 与曲线 $C$ 交于 $A$ ， $B$ 两点，求以 $A B$ 为直径的圆的极坐标方程.

查看试题解析
23. 已知函数 $f (x) = | x - 2 | + | 2 x - 1 |$ .

(1)、求不等式 $f (x) \leq 3$ 的解集；

(2)、若关于 $x$ 的不等式 $f (x) \geq a^{2} - \frac{5}{2} a$ 的解集为 $R$ ，求实数 $a$ 的取值范围.

查看试题解析