（人教版）2021-2022学年度第二学期七年级数学10.2 直方图 期末复习测试卷
试卷更新日期：2022-05-27 类型：复习试卷
一、单选题
-
1. 为了解邮政企业4月份收入的情况，随机抽取了25家邮政企业，获得了它们4月份收入（单位：百万元）的数据，并绘制成了频数直方图（如图，数据分成5组： ， ， ， ， ），现已知在这一组的数据是：10.0，10.0，10.1，10.9，10.9，11.5，11.6，11.8.则这25家邮政企业4月份收入的中位数是（ ）
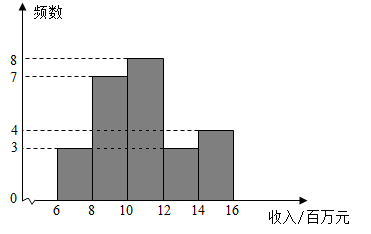A、10.0 B、10.1 C、10.9 D、11.52. 某校950名七年级学生参加跳绳测试，随机抽取部分学生成绩并绘制频数直方图（每一组含前一个边界值，不含后一个边界值）如图所示，若校方规定次数达到130次（包括130次）的成绩为“优良”，则该校成绩“优良”的学生人数约为（ ）
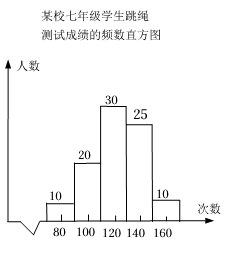A、35 B、65 C、350 D、6503. 为了解某校八年级400名学生的跳绳情况（60秒跳绳的次数），随机对该年级50名学生进行了调查，根据收集的数据绘制了如图所示的频数分布直方图（每组数据包括左端值不包括右端值，如最左边第一组的次数x为：），则以下说法正确的是（ ）
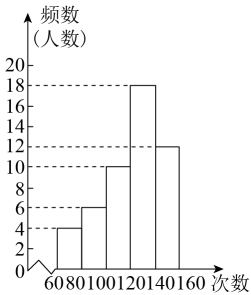A、跳绳次数不少于100次的占80% B、大多数学生跳绳次数在140~160范围内 C、跳绳次数最多的是160次 D、由样本可以估计全年级400人中跳绳次数在60~80次的大约有48人4. 小文同学统计了某栋居民楼中全体居民每周使用手机支付的次数，并绘制了频数直方图.根据图中信息﹐下列说法中错误的是（ ）
A、这栋居民楼共有居民125人 B、每周使用手机支付次数为28~35次的人数最多 C、有 的人每周使用手机支付的次数在35~42次 D、每周使用手机支付不超过21次的有15人5. 某班将安全知识竞赛成绩整理后绘制成频数直方图，图中从左至右前四组的百分比分别是4%、12 %、40%、28%，第五组的频数是8，下列结论中错误的是（ ）
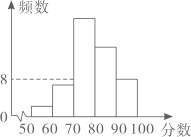A、80分以上的学生有14名 B、该班有50名同学参赛 C、成绩在70~80分的人数最多 D、第五组的百分比为16%6. 如图，一、二两组同学将本组最近5次数学平均成绩分别绘制成折线统计图.由统计图可知，成绩进步幅度大的组是（ ）
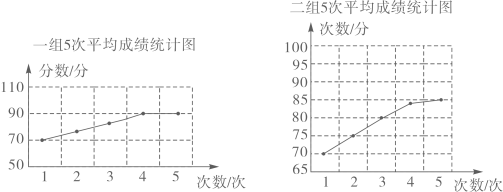A、一组 B、二组 C、一组、二组进步幅度一样大 D、无法判断7. 一组数据共40个，分为6组，第1组到第4 组的频数分别为10，5，7，6，第5组的频率为0.1，则第6组的频数为（ ）A、4 B、10 C、6 D、88. 在一篇文章中，“的”“地”“和”三个字共出现50次，已知“的”“地”出现的频率之和是0.7，那么“和”字出现的频数是（ ）A、14 B、15 C、16 D、179. 将100个数据分成8个组，如下表所示，则第六组的频数为（ ）租号
1
2
3
4
5
6
7
8
频数
11
14
12
13
13
x
12
10
A、12 B、13 C、14 D、1510. 为了解某校学生的身高情况，随机抽取该校男生、女生进行抽样调查.已知抽取的样本中，男生、女生的人数相同，利用所得数据绘制如下统计图表：身高情况分组表(单位：cm)
组别
A
B
C
D
E
身高
x＜155
155≤x＜160
160≤x＜165
165≤x＜170
x≥170
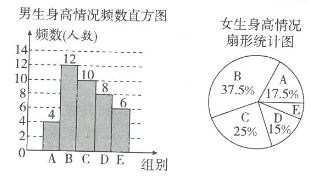
根据图表提供的信息，样本中，身高在160≤x＜170之间的女学生人数为（ ）
A、8 B、6 C、14 D、16二、填空题
-
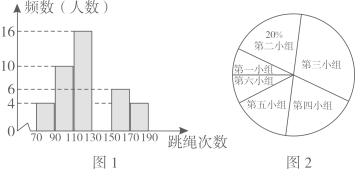
11. 已知一个40个数据的样本，把它分成6组，第一组到第四组的频数分别是10、5、7、13，第五组的频率是0.1，那么第六组的频数是.12. 一个样本有10个数据：52，51，49，50，47，48，50，51，48，53，如果组距为1.3，则应分成 组.13. 有60个数据，共分成4组，第1、2组的频数分别为25、19，第4组的频率是0.15，则第3组的频数是.14. 在实数 ，－3.14，0， 中，无理数出现的频率为15. 在大课间活动中，同学们积极参加体育锻炼，小红在全校随机抽取一部分同学就“一分钟跳绳”进行测试，并以测试数据为样本绘制成如图所示的部分频数直方图(从左到右依次分为六个小组，每小组含最小值，不含最大值)和扇形统计图.若“一分钟跳绳”次数不低于130的成绩为优秀，全校共有1 200名学生，根据图中提供的信息，估计该校学生“一分钟跳绳”成绩为优秀的人数为.
三、解答题
-
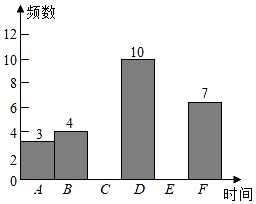
16. 某学校为了解共青团员志愿服务情况，调查小组根据平台数据进行了抽样问卷调查，过程如下：(1)、从九年级随机抽取40名共青团员，将其志愿服务时间按如下方式分组：A：0～5小时；B：5～10小时；C：10～15小时；D：15～20小时；E：20～25小时；F：25～30小时．（注：每组含最小值，不含最大值）得到这40名志愿者服务时间如下：BDEACEDBFCDDDBECDEEFAFFADCDBDFCFDECEEECE
并将上述数据整理在频数分布表中，请你补充其中的数据．
志愿服务时间
A
B
C
D
E
F
频数
3
4
10
9
7
(2)、根据上面的频数分布表，小明绘制了频数分布直方图，请将空缺的部分补充完整；(3)、分析数据：①观察以上图表，写出一个结论；
②校团委计划组织志愿服务时间不足10小时的团员参加义务劳动，根据上述信息估计九年级200名团员中参加此次义务劳动的人数约为 ▲ 人．
17. 在某段公路上，最高限速65km/h.交警部门设置了雷达探测器监测汽车的行驶速度，以下是交警部门某天一段时间内记录的驶过该处的30辆车的行驶速度（单位：km/h）；55 49 61 47 49 54 49 57 59 58
50 51 48 49 80 58 48 54 70 71
62 45 56 64 78 52 60 55 49 75
请按组距为10进行分组，列出频数分布表，画出频数分布直方图，并分析有几辆车超速.
18. 某校为了解初中学生每天在校体育活动的时间（单位：h），随机调查了该校的部分初中学生．根据调查结果，绘制出如下的统计图①和图②．请根据相关信息，解答下列问题：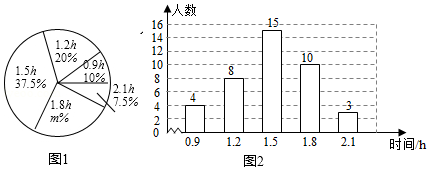
(1)、本次接受调查的初中学生人数为 ， 图①中m的值为；(2)、求统计的这组每天在校体育活动时间数据的平均数、众数和中位数；(3)、根据统计的这组每天在校体育活动时间的样本数据，若该校共有800名初中学生，估计该校每天在校体育活动时间大于1h的学生人数．19. 某校为了了解全校400名学生参加课外锻炼的情况，随机对40名学生一周内平均每天参加课外锻炼的时间进行了调查，结果如下：（单位：分）40 21 35 24 40 38 23 52 35 62 36 15 51 45 40 42 40 32 43 36 34 53 38 40 39 32 45 40 50 45 40 40 26 45 40 45 35 40 42 45
(1)、补全频率分布表和频率分布直方图．分组
频数
频率
4.5﹣22.5
2
0.050
22.5﹣30.5
3
30.5﹣38.5
10
0.250
38.5﹣46.5
19
46.5﹣54.5
5
0.125
54.5﹣62.5
1
0.025
合计
40
1.000
(2)、填空：在这个问题中，总体是 ， 样本是 ． 由统计结果分析的，这组数据的平均数是38.35（分），众数是 ， 中位数是 ．(3)、如果描述该校400名学生一周内平均每天参加课外锻炼时间的总体情况，你认为用平均数、众数、中位数中的哪一个量比较合适？(4)、估计这所学校有多少名学生，平均每天参加课外锻炼的时间多于30分？20. 为了传承中华优秀传统文化，市教育局决定开展“经典诵读进校园”活动，某校团委组织八年级100名学生进行“经典诵读”选拔赛，赛后对全体参赛学生的成绩进行整理，得到下列不完整的统计图表。组别
分数段
频次
频率
A
60⩽x<70
17
0.17
B
70⩽x<80
30
a
C
80⩽x<90
b
0.45
D
90⩽x<100
8
0.08
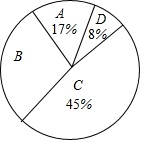
请根据所给信息，解答以下问题：
(1)、表中a= ， b=；(2)、请计算扇形统计图中B组对应扇形的圆心角的度数；(3)、已知有四名同学均取得98分的最好成绩，其中包括来自同一班级的甲、乙两名同学，学校将从这四名同学中随机选出两名参加市级比赛，请用列表法或画树状图法求甲、乙两名同学都被选中的概率。21. 初二年级教师对试卷讲评课中学生参与的深度与广度进行评价调查，其评价项目为主动质疑、独立思考、专注听讲、讲解题目四项．评价组随机抽取了若干名初二学生的参与情况，绘制成如图所示的频数分布直方图和扇形统计图（均不完整），请根据图中所给信息解答下列问题：
(1)、在这次评价中，一共抽查了名学生；(2)、在扇形统计图中，项目“主动质疑”所在的扇形的圆心角的度数为度；
(3)、请将频数分布直方图补充完整；
(4)、如果全市有6000名初二学生，那么在试卷评讲课中，“独立思考”的初二学生约有多少人？
22.为积极创建全国文明城市，某市对某路口的行人交通违章情况进行了 天的调查，将所得数据绘制成如下统计图（图2不完整）：
请根据所给信息，解答下列问题：
(1)、第 天，这一路口的行人交通违章次数是多少次？这 天中，行人交通违章 次的有多少天？(2)、请把图2中的频数直方图补充完整；(3)、通过宣传教育后，行人的交通违章次数明显减少．经对这一路口的再次调查发现，平均每天的行人交通违章次数比第一次调查时减少了 次，求通过宣传教育后，这一路口平均每天还出现多少次行人的交通违章？23. 某工厂甲、乙两个部门各有员工400人，为了解这两个部门员工的生产技能情况，进行了抽样调查，过程如下，请补充完整．收集数据
从甲、乙两个部门各随机抽取20名员工，进行了生产技能测试，测试成绩（百分制）如下：
甲 78 86 74 81 75 76 87 70 75 90 75 79 81 70 74 80 86 69 83 77
乙 93 73 88 81 72 81 94 83 77 83 80 81 70 81 73 78 82 80 70 40
整理、描述数据
按如下分数段整理、描述这两组样本数据：
成绩x
人数
部门
40≤x≤49
50≤x≤59
60≤x≤69
70≤x≤79
80≤x≤89
90≤x≤100
甲
0
0
1
11
7
1
乙
（说明：成绩80分及以上为生产技能优秀，70﹣﹣79分为生产技能良好，60﹣﹣69分为生产技能合格，60分以下为生产技能不合格）
分析数据
两组样本数据的平均数、中位数、众数如下表所示：
部门
平均数
中位数
众数
甲
78.3
77.5
75
乙
78
80.5
81
得出结论：a．估计乙部门生产技能优秀的员工人数为；b．可以推断出部门员工的生产技能水平较高，理由为 ． （至少从两个不同的角度说明推断的合理性）