（人教版）2021-2022学年度第二学期七年级数学9.3 一元一次不等式组期末复习测试卷

试卷更新日期：2022-05-27 类型：复习试卷

进入出卷网下载

一、单选题

1. 不等式组 ${\begin{array}{l} - 2 x + 3 < 1 \\ x - 1 \geq 2 \end{array}$ 的解集在数轴上表示正确的是（）

A、 B、 C、 D、

查看试题解析
2. 已知点P（a，2﹣a）关于x轴对称的点在第四象限，则a的取值范围在数轴上表示正确的是（）

A、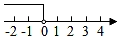 B、 C、 D、

查看试题解析
3. 若不等式组 ${\begin{array}{l} x - 2 \geq 0 \\ 2 x < m \end{array}$ 的最大整数解与最小整数解的差为3，则m的值可能为（）

A、8 B、10 C、11 D、13

查看试题解析
4. 不等式组 ${\begin{matrix} 2 x - 1 > 0 \\ x + 1 \geq 0 \end{matrix}$ 的解集是（）

A、x＞ $\frac{1}{2}$ B、﹣1≤x＜ $\frac{1}{2}$ C、x＜ $\frac{1}{2}$ D、x≥﹣1

查看试题解析
5. 如果x是一个有理数，我们定义{x}表示不小于x的最小整数．如{3.2}＝4，{﹣2.6}＝﹣2，{﹣6}＝﹣6．若m满足{2m+8}＝6，则m的取值范围是（）

A、m≤﹣1 B、﹣ $\frac{3}{2}$ ＜m≤﹣1 C、m≥﹣4 D、﹣4≤m＜﹣ $\frac{7}{2}$

查看试题解析
6. 研究表明，运动时将心率p（次）控制在最佳燃脂心率范围内，能起到燃烧脂肪并且保护心脏功能的作用．最佳燃脂心率最高值不应该超过（220﹣年龄）×0.8，最低值不低于（220﹣年龄）×0.6．以40岁为例计算，220﹣40＝180，180×0.8＝144，180×0.6＝108，所以40岁的年龄最佳燃脂心率的范围用不等式可表示为（）

A、108≤p≤144 B、108＜p＜144 C、108≤p≤190 D、108＜p＜190

查看试题解析
7. 若关于 $x$ 的一元一次不等式组 ${\begin{array}{l} x \leq a \\ \frac{3 x - 1}{2} \leq x + 3 \end{array}$ 的解集为 $x \leq a$ ，且关于 $y$ 的分式方程 $\frac{y - a}{y - 2} + \frac{3 y - 4}{y - 2} = 1$ 有正整数解，则所有满足条件的整数 $a$ 的值之积是（）

A、28 B、-14 C、7 D、56

查看试题解析
8. 关于x的不等式组 ${\begin{array}{l} \frac{2 x + 1}{3} \geq x - 1 \\ 2 x > a + 1 \end{array}$ 有且只有2个奇数解，则符合条件的所有整数a的和为（）

A、－6 B、－3 C、0 D、6

查看试题解析
9. 对于实数m，n，定义一种运算“ $※$ ”为 $m ※ n = m^{2} + m n$ ，例如， $5 ※ 3 = 5^{2} + 5 \times 3 = 40$ 那么不等式组 ${\begin{array}{l} (- 2) ※ x > 0 \\ 1 ※ x \geq 0 \end{array}$ 的解集在数轴上表示为（）

A、 B、 C、 D、

查看试题解析
10. 如果不等式组 ${\begin{array}{l} 3 - 2 x \geq 0 \\ x \geq m \end{array}$ 有解，则 $m$ 的取值范围是（）

A、 $m < \frac{3}{2}$ B、 $m \leq \frac{3}{2}$ C、 $m > \frac{3}{2}$ D、 $m \geq \frac{3}{2}$

查看试题解析

二、填空题

11. 不等式组 ${\begin{array}{l} 2 x - 8 < 0 \\ 3 - x > - 2 \end{array}$ 的解集是．

查看试题解析
12. 杭州市将在2022年举办亚运会，为加强学校体育工作，某学校决定购买一批篮球和足球共100个．已知篮球和足球的单价分别为120元和90元．根据需求，篮球购买的数量不少于40个．学校可用于购买这批篮球和足球的资金最多为10260元，则有种购买方案．

查看试题解析
13. 不等式组 ${\begin{array}{l} x - 3 > 4 \\ 6 - x < 1 \end{array}$ 的解集是．

查看试题解析
14. 小明去商店购买A、B两种玩具，共用了10元钱，A种玩具每件1元，B种玩具每件2元．若每种玩具至少买一件，且A种玩具的数量多于B种玩具的数量．则小明的购买方案有种．

查看试题解析
15. 若关于x的一元一次不等式组 ${\begin{array}{l} 2 x - a ＜ 0 \\ 3 x - 6 ＞ 0 \end{array}$ 无解，则a的取值范围是．

查看试题解析

三、解答题

16. 解不等式组 ${\begin{array}{l} 2 (x + 1) \leq 5 x + 8 \\ 2 x - 5 < \frac{x - 1}{2} \end{array}$ ，并写出它的所有整数解．

查看试题解析
17. 如果关于 $x$ 的方程 $1 + \frac{x}{2 - x} = \frac{2 m}{x^{2} - 4}$ 的解，也是不等式组 ${\begin{matrix} \frac{1 - x}{2} > x - 2 \\ 2 (x - 3) \leq x - 8 \end{matrix}$ 的解，求 $m$ 的取值范围.

查看试题解析
18. 某工厂计划生产A、B两种产品共60件，需购买甲、乙两种材料．生产一件A产品需甲种材料4千克，乙种材料1千克；生产一件B产品需甲、乙两种材料各3千克．经测算，购买甲、乙两种材料各1千克共需资金60元；购买甲种材料2千克和乙种材料3千克共需资金155元．已知工厂用于购买甲、乙两种材料的资金不能超过10000元，且生产B产品要超过38件，问有哪几种符合条件的生产方案？

查看试题解析
19. 阅读与思考：
请仔细阅读材料，并完成相应任务．
好学善思的小明和小亮同学阅读数学课外书时，看到这样一道题：
解关于x的不等式 $\frac{x + 1}{3 x - 2}$ >0．
两位同学认为这道题虽然没学过，但是可以用已学的知识解决．
小明的方法：
根据“两数相除，同号得正”，可以将原不等式转化为 ${\begin{array}{l} x + 1 > 0 \\ 3 x - 2 > 0 \end{array}$ 或 ${\begin{array}{l} x + 1 < 0 \\ 3 x - 2 < 0 \end{array}$ 解得．
小亮的方法：
将原不等式两边同时乘以（3x－2），得x＋1>0，
解得…，
任务一：你认为小明和小亮的方法正确吗?若正确请补充完整解题过程；若不正确，请说明理由．
任务二：请尝试利用已学知识解关于x的不等式∶ $\frac{x - 2}{x + 3} < 2$

查看试题解析
20. 以下是圆圆解不等式组 ${\begin{array}{l} 2 (1 + x) > - 2 ① \\ - (1 - x) > 3 ② \end{array}$ 的解答过程：解：由①，得2+x＞﹣2，所以x＞﹣4．由②，得1﹣x＞﹣3，所以﹣x＞﹣2，所以x＞2．所以原不等式组的解是x＞2．圆圆的解答过程是否有错误？如果有错误，请写出正确的解答过程．

查看试题解析
21. 一工厂要将100吨货物运往外地，计划租用某运输公司甲、乙两种型号的汽车共6辆一次将货物全部运输.已知每辆甲型汽车最多能装该种货物16吨，租金800元，每辆乙型汽车最多能装该种货物18吨，租金850元，若此工厂计划此次租车费用不超过5000元，通过计算求出该公司共有几种租车方案？请你设计出来，并求出最低的租车费用.

查看试题解析
22. 先化简，再求值： $(\frac{x^{2} + x}{x - 1} - x - 1) \div \frac{x^{2} + x}{x^{2} - 2 x + 1}$ ，其中 $x$ 为不等式组 ${\begin{array}{l} 2 (2 x + 3) - x < 12 ， \\ x \geq - 2 \end{array}$ 的整数解，挑一个合适的 $x$ 代入求值.

查看试题解析
23. 求不等式 $(2 x - 1) (x + 3) > 0$ 的解集．
解：根据“同号两数相乘，积为正”可得：① ${\begin{array}{l} 2 x - 1 > 0 \\ x + 3 > 0 \end{array}$ 或② ${\begin{array}{l} 2 x - 1 < 0 \\ x + 3 < 0 \end{array}$
解①得 $x > \frac{1}{2}$ ，解②得 $x < - 3$ ．
$∴$ 不等式的解集为 $x > 1$ 或 $x < - 3$ ．
请你仿照上述方法求不等式 $(2 x - 1) (x + 1) < 0$ 的解集．

查看试题解析

（人教版）2021-2022学年度第二学期七年级数学9.3 一元一次不等式组 期末复习测试卷

一、单选题

二、填空题

三、解答题

（人教版）2021-2022学年度第二学期七年级数学9.3 一元一次不等式组期末复习测试卷