（人教版）2021-2022学年度第二学期七年级数学7.2坐标方法的简单应用 期末复习测试卷
试卷更新日期：2022-05-27 类型：复习试卷
一、单选题
-
1. 象棋在中国有着三千多年的历史，由于用具简单，趣味性强，成为流行极为广泛的益智游戏.如图，是一局象棋残局，若“帅”位于点 ，“马”位于 ，则位于原点位置的是（ ）
A、相 B、炮 C、车 D、兵2. 根据下列表述，不能确定具体位置的是（ ）A、教室内的3排4列 B、渠江镇胜利街道15号 C、南偏西 D、东经 ，北纬3. 星城长沙是湖南省省会城市，也是长江中游地区重要的中心城市，以下能准确表示长沙地理位置的是（ ）A、在北京的西南方 B、东经112.59°，北纬28.12° C、距离北京1478千米处 D、东经112.59°4. 张强在某旅游景点的动物园的大门口看到这个动物园的平面示意图(如图所示)，若以大门为坐标原点，其他四个景点大致用坐标表示肯定错误的是（ ）
A、熊猫馆(1，4) B、猴山(6，0) C、百鸟园(5，-3) D、驼峰(3，-2)5. 如图所示是在方格纸上画出的小旗图案，若用(0，0)表示C点，(-3，2)表示B点，那么A点的位置可表示为（ ）
A、(0，-3) B、(2，-3) C、(-3，-2) D、(-3，0)6. 在平面直角坐标系中，第二象限内有一点 ，点A到x轴的距离为2，到y轴的距离为4：则m、n的值为（ ）A、 ， B、 ， C、 ， D、 ，7. 如图，在平面直角坐标系中，将先向下平移4个单位长度，再向右平移3个单位长度，则点B的对应点的坐标为（ ）
A、 B、 C、 D、8. 线段AB∥x轴，且AB＝3，若点A的坐标为（﹣2，3），则点B的坐标为（ ）A、（1，3） B、（﹣5，3） C、（1，3）或（﹣5，3） D、（﹣2，0）或（﹣2，6）9. 将二次函数 的图像向上平移2个单位后得到的新抛物线的表达式为（ ）A、 B、 C、 D、10. 如图所示，在平面直角坐标系中，△ABC位于第一象限，点A的坐标是(4，3)，把△ABC向左平移6个单位长度，得到△A1B1C1 ， 则点B1的坐标是（ ）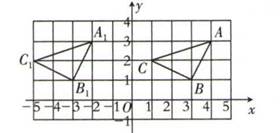
A、(-2，3) B、(3，-1) C、(-3，1) D、(-5，2)二、填空题
-
11. 如图所示，台风中心A在O地的正南方向45 km处，台风以30km/h的速度向正北方向移动．如果点A记为(0，-45)，那么2 h后台风中心的位置B记为
12. 以水平数轴的原点O为圆心，过正半轴Ox上的每一刻度点画同心圆，将Ox逆时针依次旋转30°，60°，90°……330°得到11条射线，构成如图所示的“圆”坐标系，点A，B的坐标分别表示为(5，0)，(4，300°)，则点C的坐标表示为
13. 如图所示是轰炸机机群的一个飞行队形，如果最后两架轰炸机的平面坐标分别为A(-2，1)和B(-2，-3)，那么第一架轰炸机C的平面坐标是
14. 将点向上平移3个单位，再向右平移2个单位得到点B，则点B坐标为 ．15. 如图，正方形ABCD的顶点B、C都在x轴上，若点A的坐标是（-1，4），点B的坐标是（-1，0），则点C的坐标是。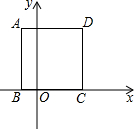
三、解答题
-
16. 春天到了，某班同学组织到公园春游，如图是公园的平面图（小正方形的边长代表100m长），图中牡丹园的坐标是（300，300），望春亭的坐标为（﹣200，﹣100），请在图中建立平面直角坐标系并写出其它地点的坐标.
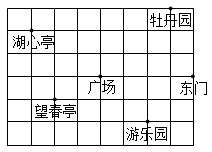17. 如图，这是某市部分简图，请以火车站为坐标原点向东的方向为 x 轴的正方向，建立平面直角坐标系，并分别写出火车站以北（包括火车站）各地点的坐标．（每个正方形边长是 1）
18. 如图是某个海岛的平面示意图，如果哨所1的坐标是（1，3），哨所2的坐标是（-2，0），请你先建立平面直角坐标系，并用坐标表示出小广场、雷达、营房、码头的位置．
19. 五子连珠棋的棋盘是15行15列的正方形，规定黑子先下，双方交替进行，在任意一个方向上，先连成5个子的一方获胜，如图所示的是两人所下的棋局的一部分，A点的位置记作（8，3），执白子的一方若想再放一子便获胜，应该把子落在什么位置？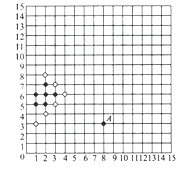
20. 如图，在平面直角坐标系中，A（-2，0），C（2，2），过C作CB⊥x轴于B，在y轴上是否存在点P，使得 和 的面积相等，若存在，求出P点的坐标；若不存在，请说明理由.
21. 已知四边形AOCD是放置在平面直角坐标系内的梯形，其中O是坐标原点，点A，C，D的坐标分别为（0，8），（5，0），（3，8）.若点P在梯形内，且△PAD的面积等于△POC的面积，△PAO的面积等于△PCD的面积. 求点P的坐标.22. 如图，已知A(－2，0)，B(4，0)，C(2，4)．D(0，2)
(1)、求三角形ABC的面积；(2)、设P为坐标轴上一点，若 ，求P点的坐标．23. 对于平面直角坐标系xOy中的点P（a，b），若点P′的坐标为（a+kb，ka+b）（其中k为常数，且k≠0），则称点P′为点P的“k属派生点”．例如：P（1，4）的“2属派生点”为P′（1+2×4，2×1+4），即P′（9，6）．
(1)、点P（﹣2，3）的“3属派生点”P′的坐标为；(2)、若点P的“5属派生点”P′的坐标为（3，﹣9），求点P的坐标；(3)、若点P在x轴的正半轴上，点P的“k属派生点”为P′点，且线段PP′的长度为线段OP长度的2倍，求k的值．