天津市津南区2021-2022学年七年级下学期期中数学试题
试卷更新日期:2022-05-26 类型:期中考试
一、单选题
-
1. 下列实数 , ,3.14159, ,0, +1,中无理数有( )A、0个 B、1个 C、2个 D、3个2. 如图所示,下列结论中正确的是 ( )
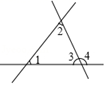 A、 和 是同位角 B、 和 是同旁内角 C、 和 是内错角 D、 和 是对顶角3. 的立方根是( )A、±4 B、±2 C、-2 D、-44. 如图,AB//CD,DE⊥CE,∠1=34°,则∠DCE的度数为( )
A、 和 是同位角 B、 和 是同旁内角 C、 和 是内错角 D、 和 是对顶角3. 的立方根是( )A、±4 B、±2 C、-2 D、-44. 如图,AB//CD,DE⊥CE,∠1=34°,则∠DCE的度数为( ) A、34° B、56° C、66° D、54°5. 如图,在数轴上表示实数 的点可能( ).
A、34° B、56° C、66° D、54°5. 如图,在数轴上表示实数 的点可能( ). A、点P B、点Q C、点M D、点N6. 已知:如图AB∥CD,EF交AB于G,交CD于F,FH平分∠EFD,交AB于H,∠AGE=50°,则∠BHF的度数为( )
A、点P B、点Q C、点M D、点N6. 已知:如图AB∥CD,EF交AB于G,交CD于F,FH平分∠EFD,交AB于H,∠AGE=50°,则∠BHF的度数为( ) A、115° B、65° C、50° D、130°7. 已知 , , 则( )A、0.15129 B、0.015129 C、0.0015129 D、1.51298. 下列说法错误的是( )A、过任意一点可作已知直线的一条平行线 B、在同一平面内两条不相交的直线是平行线 C、在同一平面内,过直线外一点只能画一条直线与已知直线垂直 D、直线外一点与直线上各点连接的所有线段中,垂线段最短9. 如图,象棋盘上,若“将”位于点(3,﹣2),“车”位于点(﹣1,﹣2),则“马”位于( )
A、115° B、65° C、50° D、130°7. 已知 , , 则( )A、0.15129 B、0.015129 C、0.0015129 D、1.51298. 下列说法错误的是( )A、过任意一点可作已知直线的一条平行线 B、在同一平面内两条不相交的直线是平行线 C、在同一平面内,过直线外一点只能画一条直线与已知直线垂直 D、直线外一点与直线上各点连接的所有线段中,垂线段最短9. 如图,象棋盘上,若“将”位于点(3,﹣2),“车”位于点(﹣1,﹣2),则“马”位于( )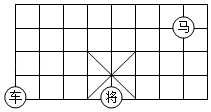 A、(1,3) B、(5,3) C、(6,1) D、(8,2)10. 在平面直角坐标系的第四象限内有一点M,到x轴的距离为4,到y轴的距离为5,则点M的坐标为( )A、 B、 C、 D、11.
A、(1,3) B、(5,3) C、(6,1) D、(8,2)10. 在平面直角坐标系的第四象限内有一点M,到x轴的距离为4,到y轴的距离为5,则点M的坐标为( )A、 B、 C、 D、11.如图,AB∥CD,直线EF与AB,CD分别交于点M,N,过点N的直线GH与AB交于点P,则下列结论错误的是( )
 A、∠EMB=∠END B、∠BMN=∠MNC C、∠CNH=∠BPG D、∠DNG=∠AME12. 如图,AF∥CD,CB平分∠ACD,BD平分∠EBF,且BC⊥BD,下列结论:① BC平分∠ABE;② AC∥BE;③ ∠CBE+∠D=90°;④ ∠DEB=2∠ABC.其中正确结论的个数有( )
A、∠EMB=∠END B、∠BMN=∠MNC C、∠CNH=∠BPG D、∠DNG=∠AME12. 如图,AF∥CD,CB平分∠ACD,BD平分∠EBF,且BC⊥BD,下列结论:① BC平分∠ABE;② AC∥BE;③ ∠CBE+∠D=90°;④ ∠DEB=2∠ABC.其中正确结论的个数有( ) A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
13. 36的平方根是.14. 将命题“同角的补角相等”改写成“如果……那么……”的形式为
15. 若点在轴上,则点的坐标是 .16. 如图,点在射线上,请你添加一个条件 , 使得 . 17. 点P的坐标为(2-a,3a+6),且点P到两坐标轴的距离相等,则点P的坐标是 .18. 如图, , 点为上一点,、的角平分线交于点 , 已知 , 则度.
17. 点P的坐标为(2-a,3a+6),且点P到两坐标轴的距离相等,则点P的坐标是 .18. 如图, , 点为上一点,、的角平分线交于点 , 已知 , 则度.
三、解答题
-
19. 如图,直线与直线交于点 , 点为直线、外一点,根据下列语句画图,并作答:
 (1)、过点画交于点;(2)、过点画 , 垂足为;(3)、点为直线上一点,连接 , 连接.20. 在中,三个顶点的坐标分别为 , , ,
(1)、过点画交于点;(2)、过点画 , 垂足为;(3)、点为直线上一点,连接 , 连接.20. 在中,三个顶点的坐标分别为 , , ,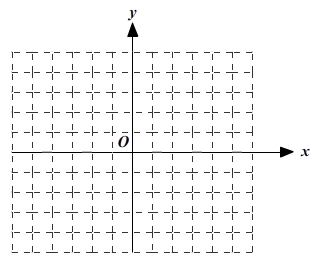 (1)、在直角坐标系描出、、三点.(2)、将沿轴负方向平移5个单位长度,再沿轴在正方向平移3个单位长度得到 , 求的三个顶点坐标.(3)、设点在坐标轴上,且与的面积相等,求点的坐标21. 计算:(1)、;(2)、22. 求下列各式中x的值:(1)、4x2-9=0;(2)、8(x-1)3=-23. 已知如图,直线AB、CD相交于点O,OE⊥CD于O,OD平分∠BOF,若∠BOE=60°,试求∠AOC和∠AOF的度数.
(1)、在直角坐标系描出、、三点.(2)、将沿轴负方向平移5个单位长度,再沿轴在正方向平移3个单位长度得到 , 求的三个顶点坐标.(3)、设点在坐标轴上,且与的面积相等,求点的坐标21. 计算:(1)、;(2)、22. 求下列各式中x的值:(1)、4x2-9=0;(2)、8(x-1)3=-23. 已知如图,直线AB、CD相交于点O,OE⊥CD于O,OD平分∠BOF,若∠BOE=60°,试求∠AOC和∠AOF的度数. 24. 填空并完成以下证明:
24. 填空并完成以下证明:如图,∠1=∠ACB,∠2=∠3,FH⊥AB于H,求证:CD⊥AB.

证明:∵FH⊥AB(已知),
∴∠BHF= ▲ .
∵∠1=∠ACB(已知),
∴DE∥BC,( )
∴∠2= ▲ . ( )
∵∠2=∠3(已知),
∴∠3= ▲ , ( )
∴CD∥FH( )
∴∠BDC=∠BHF= ▲ °,( )
∴CD⊥AB.

