山东省聊城市临清市2021-2022学年七年级下学期期中数学试题

试卷更新日期：2022-05-26 类型：期中考试

进入出卷网下载

一、单选题

1. 若 $∠ A = 48 °$ ，则 $∠ A$ 的补角的度数为（）

A、42° B、52° C、132° D、142°

查看试题解析
2. 若 ${\begin{array}{l} x = 1 \\ y = 2 \end{array}$ 是关于x 、y的二元一次方程ax－2y＝1的解，则a的值为（）

A、3 B、5 C、－3 D、－5

查看试题解析
3. 如图，直线AB，CD相交于点O， $O E ⊥ C D$ 于点O， $∠ 1 = 40 °$ ，则 $∠ A O C$ 的度数（）

A、50° B、120° C、130° D、140°

查看试题解析
4. 如图，AD是∠EAC的平分线，AD∥BC，∠B=35°，则∠C的度数为（）

A、55° B、45° C、35° D、25°

查看试题解析
5. 已知x，y满足方程组 ${\begin{cases} 2 x + 3 y = - 1 \\ 3 x + 4 y = 3 \end{cases}$ ，则 $x + y$ 的值为（）

A、4 B、3 C、2 D、 $- 4$

查看试题解析
6. 如图，将一张长方形纸片ABCD沿EF折叠，点A、B分别落在点 $A^{'}$ 、 $B^{'}$ 处，若 $∠ 1 = 65 °$ ，则 $∠ A^{'} E D$ 的度数是（）

A、65° B、60° C、50° D、57.5°

查看试题解析
7. 下列运算正确的是（）

A、 $a^{2} \cdot a^{3} = a^{6}$ B、 ${(- y^{2})}^{3} = y^{6}$ C、 ${(m^{2} n)}^{3} = m^{5} n^{3}$ D、 ${(- a)}^{6} \div a^{3} = a^{3}$

查看试题解析
8. $(3 x + 2 y) (k x - y)$ 的展开式中不含xy项，则k的值是（）

A、 $- \frac{3}{2}$ B、 $\frac{3}{2}$ C、 $- \frac{2}{3}$ D、 $\frac{2}{3}$

查看试题解析
9. 已知∠A、∠B互余，∠A比∠B大30°．则∠B的度数为（　　）

A、30° B、40° C、50° D、60°

查看试题解析
10. 下列说法正确的是（）

A、相等的角是对顶角 B、正常走动的时钟，分针每分钟旋转6° C、如果 $a ⊥ b$ ， $b ⊥ c$ ，那么 $a ⊥ c$ D、P是直线a外一点，A、B、C分别是a上的三点， $P A = 1$ ， $P B = 2$ ， $P C = 3$ ，则点P到直线a的距离是1

查看试题解析
11. 《九章算术》是中国古代的一本重要数学著作，其中有一道方程的应用题：“五只雀、六只燕，共重16两，雀重燕轻．互换其中一只，恰好一样重．问每只雀、燕的重量各为多少？”解：设雀每只x两，燕每只y两，则可列出方程组为（）

A、 ${\begin{array}{l} 5 x + 6 y = 16 \\ 5 x + y = 6 y + x \end{array}$ B、 ${\begin{array}{l} 5 x + 6 y = 16 \\ 4 x + y = 5 y + x \end{array}$ C、 ${\begin{array}{l} 6 x + 5 y = 16 \\ 6 x + y = 5 y + x \end{array}$ D、 ${\begin{array}{l} 6 x + 5 y = 16 \\ 5 x + y = 4 y + x \end{array}$

查看试题解析
12. 如图，已知AB∥CD，则∠α、∠β和∠γ之间的关系为（）

A、β＋γ－α＝180° B、α＋γ＝β C、α＋β＋γ＝360° D、α＋β－2γ＝180°

查看试题解析

二、填空题

13. 如图，如果 $∠ A +$ $= 180 °$ ，那么 $A D ∥ B C$ ．

查看试题解析
14. 若 $∠ 1 = 18 ° 1 8^{'}$ ， $∠ 2 = 18.18 °$ ，则 $∠ 1$ $∠ 2$ ．（填>、<、=）

查看试题解析
15. 若 $(x + 4) (x - 3) = x^{2} + m x + n$ ，则 $m =$ ， $n =$ ．

查看试题解析
16. 若 ${(2 x - y)}^{2}$ 与 $| x + 2 y - 5 |$ 互为相反数，则 ${(x - y)}^{2021} =$ ．

查看试题解析
17. 如图，某市有一块长为 $(3 a + b)$ 米，宽为 $(2 a + b)$ 米的长方形地块，规划部门计划将阴影部分进行绿化，中间将修建一座雕像，则绿化面积是平方米．

查看试题解析

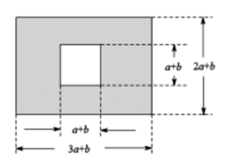
三、解答题

18. 解下列二元一次方程组：

(1)、 ${\begin{cases} y = 2 x + 3 \\ 3 x + y = 18 \end{cases}$ ；

(2)、 ${\begin{cases} \frac{x}{2} + \frac{y}{3} = 2 \\ 4 (x + y) = 20 \end{cases}$ ．

查看试题解析
19. 计算：

(1)、 ${(3 a)}^{2} \cdot a^{4} - {(- a^{3})}^{2}$ ；

(2)、 $2 x (x + 1) - (3 x - 1) (x - 5)$ ．

查看试题解析
20. 如图，已知BD平分 $∠ A B C$ ， $E D ∥ B C$ ， $∠ A E D = 50 °$ ．求 $∠ E D B$ 的度数．

查看试题解析
21. 如图，点O是直线AB上的一点，OC是 $∠ A O D$ 的平分线， $O C ⊥ O E$ ，且 $∠ A O D = 80 °$ ，求 $∠ B O E$ 的度数．

查看试题解析
22. 已知 $2^{m} = a$ ， $2^{n} = b$ ，

(1)、求 $2^{3 m + 2 n}$ ；（结果用含a，b的代数式表示）

(2)、求 $4^{m + n - 2}$ ．（结果用含a，b的代数式表示）

查看试题解析
23. 已知关于x，y的二元一次方程组 ${\begin{cases} 3 x + 5 y = m + 2 \\ 2 x + y = m \end{cases}$ 的解适合 $x + y = 5$ ，求m的值．

查看试题解析
24. 为了提倡节约用水，某市对居民用水采用分段计费方式：当每户每月用水量不超过 $12 m^{3}$ 时，按一级单价收费；当每户每月用水量超过 $12 m^{3}$ 时，超过部分按二级单价收费.已知李阿姨家五月份用水量为 $14 m^{3}$ ，缴纳水费38.2元．七月份用水量为 $18 m^{3}$ ，缴纳水费52.2元．

(1)、问该市一级水费，二级水费的单价分别是多少元？

(2)、若该市某户十月份用水量为 $22 m^{3}$ ，求该户这个月应缴纳水费多少元？

查看试题解析
25. 如图，在 $6 \times 6$ 的正方形网格中，每个小正方形的边长是1，点M、N、P、Q均为格点（格点是指每个小正方形的顶点），线段MN经过点P．

(1)、过点P画MN的垂线；

(2)、过点Q画MN的平行线；

(3)、若格点F使△PFM的面积等于4，则这样的点F共有个．

查看试题解析
26. 已知 $A B ∥ C D$ ．

(1)、如图1， $∠ 1 = ∠ 2$ 吗？为什么？

(2)、如图2， $∠ B = ∠ C$ ．试判定BE与CF的位置关系，并说明理由．

查看试题解析