广东省河源市紫金县2021-2022学年七年级下学期期中数学试题
试卷更新日期:2022-05-26 类型:期中考试
一、单选题
-
1. 已知 ,则 的余角等于( )A、 B、 C、 D、2. 某种冠状病毒的直径约为0.00000012米,将0.00000012用科学记数法表示为( )A、 B、 C、 D、3. 下列运算正确的是( )A、 B、 C、 D、4. 下列各式能用平方差公式计算的是 ( )A、 B、 C、 D、5. 如图,测量运动员跳远成绩选取的是AB的长度,其依据是( )
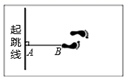 A、两点确定一条直线 B、垂线段最短 C、两点之间线段最短 D、两点之间直线最短6. 小李骑车沿直线旅行,先前进了1000米,休息了一段时间,又原路返回800米,再前进1200米,则他离起点的距离s与时间t的关系示意图是( )A、
A、两点确定一条直线 B、垂线段最短 C、两点之间线段最短 D、两点之间直线最短6. 小李骑车沿直线旅行,先前进了1000米,休息了一段时间,又原路返回800米,再前进1200米,则他离起点的距离s与时间t的关系示意图是( )A、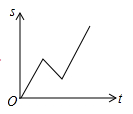 B、
B、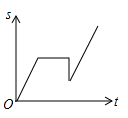 C、
C、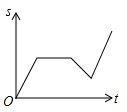 D、
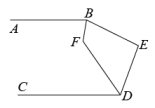
D、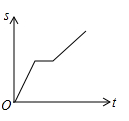 7. 如图, 的度数为( )
7. 如图, 的度数为( )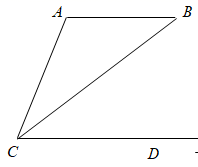 A、 B、 C、 D、8. 下表是研究弹簧长度与所挂物体质量关系的实验表格:
A、 B、 C、 D、8. 下表是研究弹簧长度与所挂物体质量关系的实验表格:所挂物体重量x(kg)
1
2
3
4
5
弹簧长度y(cm)
10
12
14
16
18
则弹簧不挂物体时的长度为( ).
A、4cm B、6cm C、8cm D、10cm9. 如果的展开式中不含项,那么p的值是( )A、1 B、 C、2 D、10.如图,正方形卡片A类,B类和长方形卡片C类若干张,如果要拼一个长为(a+2b),宽为(a+b)的大长方形,则需要C类卡片张数为( )
 A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4二、填空题
-
11. 计算 .12. 计算(2xy)3÷2xy2= .13. 在一定条件下,若物体运动的路程s(m)与时间t(s)之间的关系式为 , 则当时,该物体所经过的路程为m.14. 一个长方体的底面是一个边长为10cm的正方形,如果高为h(cm)时,体积为V(cm3),则V与h的关系为;15. 如图,在条件:①;②;③;④中,能判断的条件是(填序号).
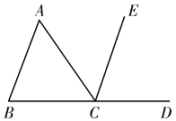 16. 如果x2-mx+16是一个完全平方式,那么m的值为 .17. 将一张长方形纸条沿折叠后,与交于点,若 , 则的度数是 .
16. 如果x2-mx+16是一个完全平方式,那么m的值为 .17. 将一张长方形纸条沿折叠后,与交于点,若 , 则的度数是 .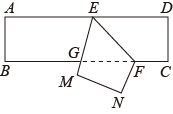
三、解答题
-
18. 利用乘法公式进行简便计算:(1)、;(2)、19. 先化简,再求值: ,其中 , .20. 如图,一块大的三角形广告牌,D是上一点,现要求过点D设计出一块小的三角形 , 使 .
 (1)、请用尺规作出 . (不写作法,保留作图痕迹)(2)、若 , 求的度数.21. “已知am=4,am+n=20,求an的值.”这个问题,我们可以这样思考:逆向运用同底数幂的乘法公式,可得: am+n=aman , 所以20=4an , 所以an=5.
(1)、请用尺规作出 . (不写作法,保留作图痕迹)(2)、若 , 求的度数.21. “已知am=4,am+n=20,求an的值.”这个问题,我们可以这样思考:逆向运用同底数幂的乘法公式,可得: am+n=aman , 所以20=4an , 所以an=5.请利用这样的思考方法解决下列问题:
已知am=3,an=5,求下列代数的值:
(1)、a2m+n;(2)、am-3n .22. 将一幅三角板拼成如图所示的图形,过点C作CF平分∠DCE交DE于点F, (1)、求证:CF∥AB,(2)、求∠DFC的度数.23. 某机动车出发前油箱内有油42L.行驶若干小时后,途中在加油站加油若干升.油箱中剩余油量Q(L)与行驶时间t(h)之间的关系如图所示,根据图象回答下列问题.
(1)、求证:CF∥AB,(2)、求∠DFC的度数.23. 某机动车出发前油箱内有油42L.行驶若干小时后,途中在加油站加油若干升.油箱中剩余油量Q(L)与行驶时间t(h)之间的关系如图所示,根据图象回答下列问题. (1)、在这个变化过程中,是自变量,是因变量;(2)、机动车行驶小时后加油,中途加油 L;(3)、如果加油站距目的地还有240km,车速为40km/h,要到达目的地,请判断油箱中的油是否够用,并说明理由.24. 如图①所示是一个长为2m、宽为2n的长方形,沿图中虚线用剪刀均分成4个小长方形,然后按图②的方式拼成一个正方形.
(1)、在这个变化过程中,是自变量,是因变量;(2)、机动车行驶小时后加油,中途加油 L;(3)、如果加油站距目的地还有240km,车速为40km/h,要到达目的地,请判断油箱中的油是否够用,并说明理由.24. 如图①所示是一个长为2m、宽为2n的长方形,沿图中虚线用剪刀均分成4个小长方形,然后按图②的方式拼成一个正方形.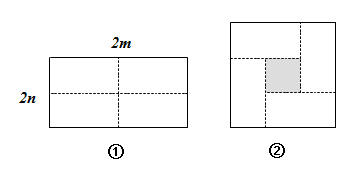 (1)、请用两种不同的方式表示图②中阴影部分的面积.
(1)、请用两种不同的方式表示图②中阴影部分的面积.方法1:;
方法2:;
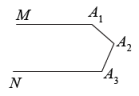
(2)、由(1)写出、、这三个代数式之间的等量关系:;(3)、利用(2)中得到的等量关系,解决如下问题:若 , , 求;(4)、填空:若 , 则 .25.(1)、如图1, , 则 ;
如图2, , 则 ;
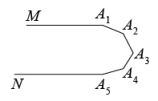
如图3, , 则 ;

如图4, , 则 .
 (2)、如图5, , 则 .
(2)、如图5, , 则 .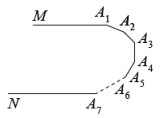 (3)、利用上述结论解决问题:如图6,已知 , ∠ABE和∠CDE的平分线相交于点F, , 求∠BFD的度数.
(3)、利用上述结论解决问题:如图6,已知 , ∠ABE和∠CDE的平分线相交于点F, , 求∠BFD的度数.