山东省临沂市河东区2021-2022学年八年级下学期期中数学试题

试卷更新日期：2022-05-26 类型：期中考试

进入出卷网下载

一、单选题

1. 下列各式成立的是（）

A、 $\sqrt{(- 3)^{2}} = - 3$ B、 $\sqrt{x^{2}} = x$ C、 $\sqrt{(- 5)^{2}} = 5$ D、 $\sqrt{a^{2} + 1} = a + 1$

查看试题解析
2. 如果m是任意实数，那么下列代数式中一定有意义的是（　　）

A、 $\sqrt{m}$ B、 $\sqrt{m + 1}$ C、 $\frac{1}{m + 1}$ D、 $\sqrt{m^{2} + 1}$

查看试题解析
3. 如图，下列四组条件中，不能判定四边形 $A B C D$ 是平行四边形的是（）

A、 $A D = B C ， A D ∥ B C$ B、 $A D ∥ B C ， A B = D C$ C、 $A D = B C ， A B = D C$ D、 $A D ∥ B C ， A B ∥ D C$

查看试题解析
4. 如图，矩形 $A B C D$ 的对角线 $A C$ 、 $B D$ 相交于点 $O$ ， $C E / / B D$ ， $D E / / A C$ ，若 $A C = 2$ ，则四边形 $O C E D$ 的周长为（）

A、1 B、2 C、3 D、4

查看试题解析
5. 如图，在四边形 $A B C D$ 中， $A B = 2$ ， $B C = 2$ ， $C D = 4$ ， $D A = 2 \sqrt{6}$ ，且 $∠ A B C = 90 °$ ，则四边形 $A B C D$ 的面积是（）

A、4 B、 $1 + 2 \sqrt{2}$ C、 $2 + 4 \sqrt{2}$ D、 $1 + \sqrt{2}$

查看试题解析
6. 等式 $\sqrt{\frac{3 - x}{x + 2}} = \frac{\sqrt{3 - x}}{\sqrt{x + 2}}$ 成立的条件是（）

A、 $- 2 < x \leq 3$ B、 $- 2 \leq x \leq 3$ C、 $x > - 2$ D、 $x \leq 3$

查看试题解析
7. 实数a，b在数轴上的位置如图所示，则化简 $\sqrt{a^{2}}$ ﹣ $\sqrt{b^{2}}$ ﹣ $\sqrt{(a - b)^{2}}$ 的结果是（）

A、2b B、2a C、2（b﹣a） D、0

查看试题解析
8. 一根长 $18 c m$ 的牙刷置于底面直径为 $5 c m$ 、高为 $12 c m$ 的圆柱形水杯中，牙刷露在杯子外面的长度为 $h c m$ ，则h的取值范围是（）

A、 $5 < h \leq 6$ B、 $6 < h \leq 7$ C、 $5 \leq h \leq 6$ D、 $5 \leq h < 6$

查看试题解析
9. 2002年8月在北京召开的国际数学家大会会徽取材于我国古代数学家赵爽的弦图，它是由四个全等的直角三角形和中间的小正方形拼成的大正方形.如图所示，如果大正方形的面积是100，小正方形的面积为20，那么每个直角三角形的周长为（）

A、 10+ $\sqrt{180}$ B、10+ $\sqrt{200}$ C、10+ $\sqrt{160}$ D、24

查看试题解析
10. 如图，正方形 $A B C D$ 的边长为4，点M在边 $D C$ 上， $D M = 1$ ，点N是对角线 $A C$ 上一动点，则线段 $D N + M N$ 的最小值为（）

A、5 B、 $4 \sqrt{2}$ C、 $\sqrt{17}$ D、4

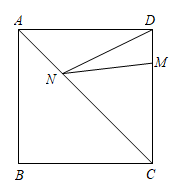查看试题解析
11. 如图，将两条宽度都为3的纸条重叠在一起，使 $∠ A B C = 60 °$ ，则四边形 $A B C D$ 的面积为（）

A、9 B、 $6 \sqrt{3}$ C、12 D、 $12 \sqrt{3}$

查看试题解析
12. 如图，将一个边长为4和8的长方形纸片ABCD折叠，使C点与A点重合，则折痕EF的长是（）

A、 $\sqrt{3}$ B、 $2 \sqrt{3}$ C、 $\sqrt{5}$ D、 $2 \sqrt{5}$

查看试题解析

二、填空题

13. 若 $x = \sqrt{2} - 1$ ，则 $x^{2} + 4 x + 1$ 的值为．

查看试题解析
14. 如图，在Rt△ABC中，∠ACB=90°，若AB=10，则正方形ADEC和正方形BCFG的面积和为.

查看试题解析
15. 先化简再求值：当 $a = - 2$ 时，求 $a + \sqrt{1 - 2 a + a^{2}}$ 的值，甲乙两人的解答如下：
甲的解答为：原式 $= a + \sqrt{(1 - a)^{2}} = a + (1 - a) = 1$ ；
乙的解答为：原式 $= a + \sqrt{(1 - a)^{2}} = a + (a - 1) = 2 a - 1 = - 5$ ．
两种解答中，的解答是错误的；
若 $a = 100$ 时， $a + \sqrt{(1 - a)^{2}} =$ ．

查看试题解析
16. 甲、乙两艘客轮分别用 $20 m / m i n$ 和 $15 m / m i n$ 速度同时离开港口，甲、乙客轮分别都用 $40 m i n$ 到达A、B两点，若A，B两点的直线距离为 $1000 m$ ，甲客轮沿着北偏东 $30 °$ 的方向航行，则乙客轮的航行方向可能是．（只填序号）
①北偏西 $60 °$ ②南偏西 $30 °$ ③南偏东 $60 °$ ④南偏西 $60 °$

查看试题解析

三、解答题

17. 计算：

(1)、 $\sqrt{\frac{2}{3}} - (\frac{1}{6} \sqrt{24} - \frac{3}{2} \sqrt{12}) + (\sqrt{3} - \sqrt{2}) (\sqrt{3} + \sqrt{2})$ ．

(2)、a，b分别是 $7 - \sqrt{5}$ 的整数部分和小数部分，求 $2 a^{2} - b$ 的值．

查看试题解析
18. 如图，用一个面积为a的正方形和四个相同的长方形拼成一个面积为 $4 a$ 的正方形图案，求一个长方形的周长．

查看试题解析
19. 在正方形网格中，每个小正方形的边长都是1．

(1)、在图中画线段 $E F$ ，使得E、F都在格点上，且 $E F = \sqrt{5}$ ；

(2)、以 $A B 、 C D 、 E F$ 三条线段能否构成直角三角形？请说明理由．

查看试题解析
20. 图①是用硬纸板做成的两个全等的直角三角形，两条直角边的长分别为a和b，斜边为c．图②是以c为直角边的等腰直角三角形．请你开动脑筋，将它们拼成一个直角梯形．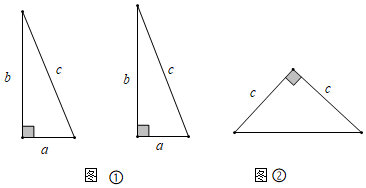

(1)、画出拼成的这个图形的示意图，并标注相关数据；

(2)、利用（1）中画出的图形证明勾股定理．

查看试题解析
21. 有一个直角三角形纸片 $A B C$ ， $∠ C = 90 °$ ，两直角边 $A C = 6 c m$ ， $B C = 8 c m$ ．

(1)、如图1，若将 $△ A B C$ 沿着直线 $D E$ 折叠，使顶点 $B$ 与点 $A$ 重合，求 $C E$ 的长；

(2)、如图2，若将 $△ A B C$ 沿直线 $A F$ 折叠，使 $A C$ 落在斜边 $A B$ 上，且与 $A G$ 重合，求 $△ A C F$ 的面积．

查看试题解析
22. 如图l，已知正方形ABCD的对角线AC、BD相交于点O，E是AC上一点，连结EB，过点A作AM $⊥$ BE，垂足为M，AM交BD于点F.

(1)、求证：OE=OF；

(2)、如图2，若点E在AC的延长线上，AM $⊥$ BE于点M，交DB的延长线于点F，其它条件不变，则结论“OE=OF”还成立吗.如果成立，请给出证明；如果不成立，请说明理由.

查看试题解析
23. 【归纳猜想】
在探究矩形的性质时，小明得到了一个有趣的结论：矩形两条对角线的平方和等于四条边的平方和．如图1，在矩形 $A B C D$ 中，由勾股定理，得 $A C^{2} = A B^{2} + B C^{2}$ ， $B D^{2} = A B^{2} + A D^{2}$ ，因为 $D C = A B$ ， $A D = B C$ ，所以 $A C^{2} + B D^{2} = A B^{2} + B C^{2} + C D^{2} + A D^{2} = 2 (A B^{2} + B C^{2})$ ．
小亮对菱形进行了探究，也得到了同样的结论，于是小亮猜想：任意平行四边形两条对角线的平方和等于四条边的平方和．
【探究发现】
求证：平行四边形两对角线的平方和等于四条边的平方和，请结合图2，写出已知、求证、并写出证明过程．

查看试题解析