广东省清远市2021-2022学年八年级下学期期中数学试题
试卷更新日期：2022-05-26 类型：期中考试
一、单选题
-
1. 下列图形中，既是轴对称图形又是中心对称图形的是（ ）A、
B、
C、
D、
2. 若 ，则下列式子一定成立的是（ ）A、 B、 C、 D、3. 在△ABC中，∠B=∠C，AB=5．则AC=（ ）A、12 B、9 C、5 D、24. 把不等式
≥
在数轴上表示出来，正确的是（ ） A、
B、
C、
D、
5. 如图，在中， ， ， ， 则（ ）
A、2 B、 C、 D、1.56. 将点P（－5，4）向右平移4个单位，得到点P的对应点P′的坐标是（ ）A、（－5，8） B、（－1，4） C、（－9，4） D、（－5，0）7. 下列命题中，其逆命题是假命题的是（ ）A、角平分线上的点到这个角两边的距离相等； B、如果a=0，b=0，那么ab=0； C、等边对等角 ； D、有两个角互余的三角形是直角三角形。8. 如图，在△ABC中，AD平分∠BAC，DE⊥AB于E， =15，DE=3，AB=6，则AC长是（ ）
A、4 B、5 C、6 D、79. 若不等式组 的解集是x＞1，则m的取值范围是（ ）A、m≥1 B、m≤1 C、m≥0 D、m≤010. 如图，在△ABC中，∠CAB＝65°，将△ABC在平面内绕点A旋转到△AB'C'的位置，使CC′∥AB，则旋转角的度数为（ ）
A、35° B、40° C、50° D、65二、填空题
-
11. 表示实数a与1的和不大于10的不等式是 ．12. 如果等腰三角形的两边长分别是2、7，那么三角形的周长是 ．13.
如图，在△ABC中，AD⊥BC，CE⊥AB，垂足分别为D，E，AD与CE交于点F，请你添加一个适当的条件： （答案不唯一），使△ADB≌△CEB．
14. 不等式组的最小整数解是 ．15. 如图所示，在△ABC中，∠C＝90°，AD平分∠BAC，DE⊥AB于E，DE＝4，BC＝9，则BD的长为 ．
16. 在平面直角坐标系xOy中，一次函数y＝kx和y＝﹣x+3的图象如图所示，则关于x的一元一次不等式kx＜﹣x+3的解集是.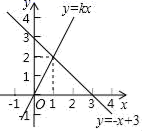
17. 如图中的螺旋由一系列直角三角形组成，则第n个三角形的面积为 ．
三、解答题
-
18. 解不等式 ， 并把它的解集表示在数轴上．
19. 解一元一次不等式组： ．20. △ABC在平面直角坐标系xOy中的位置如图所示.
(1)、作△ABC关于点O成中心对称的△A1B1C1；(2)、作出将△A1B1C1向右平移3个单位，再向上平移4个单位后的△A2B2C2；(3)、请直接写出点B2 关于x轴对称的点的坐标.21. 每年的4月23日是联合国教科文组织确定的“世界读书日”，又称“世界图书和版权日”．红星中学在“世界读书日”开展“弘扬传统文化，阅读经典名著”主题活动，计划购置一批书籍．已知每本《诗经》25元，每本《论语》18元，该学校决定购买《诗经》和《论语》共100本，总费用不超过2000元，那么该学校最多可以购买《诗经》多少本？22. 如图，在等边三角形ABC中，点D，E分别在边BC，AC上，且DE∥AB，过点E作EF⊥DE，交BC的延长线于点F．
(1)、求∠F的度数；(2)、若CD＝2，求DE的长．23. 如图，已知∠BAC=60° ，∠B=80° ，DE垂直平分AC交BC于点D，交AC于点E.
(1)、求∠BAD的度数；
(2)、若AB=10，BC=12，求△ABD的周长.
