北京市燕山区2021-2022学年八年级下学期期中考试数学试题

试卷更新日期：2022-05-26 类型：期中考试

进入出卷网下载

一、单选题

1. 下列图形中，不是轴对称图形的是（）

A、矩形 B、菱形 C、平行四边形 D、正方形

查看试题解析
2. 如图， ▱ ABCD中，AD＝4，AB＝2，则 ▱ ABCD的周长为（）

A、6 B、8 C、12 D、14

查看试题解析
3. 下列根式中，化简后可以与 $\sqrt{2}$ 合并的是（）

A、 $\sqrt{4}$ B、 $\sqrt{8}$ C、 $\sqrt{12}$ D、 $\sqrt{27}$

查看试题解析
4. 下列运算正确的是（）

A、 $\sqrt{2} + \sqrt{3} = \sqrt{5}$ B、 $\sqrt{3} - \sqrt{2} = 1$ C、 $\sqrt{2} \times \sqrt{3} = \sqrt{5}$ D、 $\sqrt{24} \div \sqrt{8} = \sqrt{3}$

查看试题解析
5. 下列各组数中，能作为直角三角形三边的是（）

A、1，2，3 B、4，5，6 C、 $\sqrt{5}$ ， $\sqrt{12}$ ， $\sqrt{13}$ D、1， $\sqrt{3}$ ， 2

查看试题解析
6. 如图，Rt△ABC中，∠ABC＝90°，点O是斜边AC的中点，AC＝10，则OB＝（）

A、5 B、6 C、8 D、10

查看试题解析
7. 如图， ▱ ABCD中，点O是对角线AC的中点，点E是BC的中点，CD＝8，则OE＝（）

A、3 B、4 C、5 D、7

查看试题解析
8. 已知菱形的两条对角线长分别为6cm 和8cm ，则菱形的边长为（）

A、10cm B、8cm C、6cm D、5cm

查看试题解析
9. 有下列四个条件：①对角线互相平分的四边形；②对角线互相垂直的四边形；③对角线相等的平行四边形；④有一个角是直角的平行四边形，其中能作为矩形的判定条件的是（）

A、①② B、③④ C、①③ D、②④

查看试题解析
10. 把图1中的菱形沿对角线分成四个全等的直角三角形，将这四个直角三角形分别拼成如图2，图3所示的正方形，则图1中菱形的面积为（）.

A、6 B、8 C、12 D、24

查看试题解析

二、填空题

11. 二次根式 $\sqrt{x - 1}$ 在实数范围内有意义，则x的取值范围是．

查看试题解析
12. 计算： ${(\sqrt{5})}^{2} =$ ， $\sqrt{{(- 8)}^{2}} =$ ．

查看试题解析
13. 如果 $| a - 3 | + \sqrt{b - 2} = 0$ ，那么 $a^{b}$ 的值是．

查看试题解析
14. 比较大小： $2 \sqrt{3}$ $3 \sqrt{2}$ （填“＞”、“＜”或“＝”）.

查看试题解析
15. 如图，四边形ABCD中，AB∥CD ，要使四边形ABCD为平行四边形，则可添加的条件为.(填一个即可)

查看试题解析
16. 一艘船以20海里/时的速度从A港向东北方向航行，另一艘船以15海里/时的速度从A港向西北方向航行，经过1小时后，它们相距海里．

查看试题解析
17. 如图，点E在正方形ABCD中，△BEC是等边三角形，则∠EAD＝°．

查看试题解析

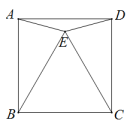18. 在数学课上，老师提出如下问题：

尺规作图：过直线外一点作已知直线的平行线．

已知：直线l及其外一点A．

求作：l的平行线，使它经过点A．

小云的作法如下：

⑴在直线l上任取一点B；

⑵以B为圆心，BA长为半径作弧，交直线l于点C；

⑶分别以A、C为圆心，BA长为半径作弧，两弧相交于点D；

⑷作直线AD．

直线AD即为所求．

小云作图的依据是．

查看试题解析

三、解答题

19. 计算：

(1)、 $\sqrt{18} - \sqrt{2}$ ；

(2)、 $\sqrt{20} \div \sqrt{5} \times \sqrt{\frac{1}{2}}$ ．

查看试题解析
20. 已知 $a = \sqrt{7} + 2$ ， $b = \sqrt{7} - 2$ ，求 $a^{2} + b^{2} - a b$ 的值．

查看试题解析
21. 如图，在平行四边形ABCD中，点E、F是对角线BD上的两点，且 $B E = D F$ ，求证：四边形AECF是平行四边形．

查看试题解析
22. 如图，四边形ABCD中，AB＝6，BC＝8，CD＝24，AD＝26，∠B＝90°，求四边形ABCD的面积．

查看试题解析
23. 春节期间，乐乐帮妈妈挂灯笼时，发现，如图长2.5米的梯子 $A B$ 斜靠在一竖直的墙 $A C$ 上，这时 $B C$ 为1.5米，当梯子的底端B向右移动0.5米到D处时，你能帮乐乐算算梯子顶端A下滑多少米吗？（E处）．

查看试题解析
24. 如图，在平行四边形ABCD中，CE⊥AD于点E，延长DA至点F，使得EF＝DA，连接BF，CF．

(1)、求证：四边形BCEF是矩形；

(2)、若AB＝3，CF＝4，DF＝5，求EF的长．

查看试题解析
25. 阅读材料：
如果一个三角形的三边长分别为a，b，c，记半周长为p，即 $p = \frac{a + b + c}{2}$ ，那么这个三角形的面积 $S = \sqrt{p (p - a) (p - b) (p - c)}$ ，这个公式叫“海伦公式”，它是利用三角形的三条边长直接求三角形面积的公式．中国南宋数学家秦九韶也得出了类似的公式，称“三斜求积术”，所以这个公式也称为“海伦—秦九韶公式”．
完成下列问题：
如图，△ABC中，三边长分别为a＝7，b＝5，c＝6．

(1)、求△ABC的面积；

(2)、过点C作CD⊥AB，垂足为点D，请补全图形，并求线段BD的长．

查看试题解析
26. 我们规定：一组邻边相等且对角互补的四边形叫做完美四边形．

(1)、在以下四种四边形中，一定是完美四边形的是（请填序号）；
①平行四边形 ②菱形 ③矩形 ④正方形

(2)、如图1，菱形ABCD中，∠A＝60°，E，F分别是AB，BC上的点，且AE＝BF，求证：四边形DEBF是完美四边形；

(3)、完美四边形ABCD中，AB＝AD，∠BAD+∠BCD＝180°，连接AC．
①如图2，求证：CA平分∠DCB；
②如图3，当∠BAD＝90°时，直接用等式表示出线段AC，BC，CD之间的数量关系．

查看试题解析