北京市海淀区2021-2022学年八年级下学期期中数学试题
试卷更新日期:2022-05-26 类型:期中考试
一、单选题
-
1. 下列各组数中,以它们为边长的线段能构成直角三角形的是( )A、2,3,4 B、 , , C、1, , 3 D、5,12,132. 下列等式,正确的是( )A、 B、 C、 D、3. 如图,在▱ABCD中,AB=4,BC=7,∠ABC的平分线交AD于点E , 则ED等于( )
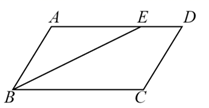 A、2 B、3 C、4 D、54. 如图,CD是的中线,E,F分别是AC,DC的中点, , 则BD的长为( )
A、2 B、3 C、4 D、54. 如图,CD是的中线,E,F分别是AC,DC的中点, , 则BD的长为( ) A、1 B、2 C、3 D、45. 如图,在正方形ABCD中,等边的顶点E,F分别在边BC和CD上,则等于( )
A、1 B、2 C、3 D、45. 如图,在正方形ABCD中,等边的顶点E,F分别在边BC和CD上,则等于( )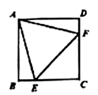 A、 B、 C、 D、6. 如图,在平面直角坐标系中,已知点O(0,0),A(2,3),以点O为圆心,OA长为半径画弧,交x轴的正半轴于B点,则B点的横坐标介于( )
A、 B、 C、 D、6. 如图,在平面直角坐标系中,已知点O(0,0),A(2,3),以点O为圆心,OA长为半径画弧,交x轴的正半轴于B点,则B点的横坐标介于( )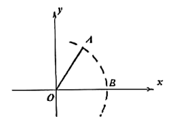 A、3和4之间 B、4和5之间 C、5和6之间 D、6和7之间7. 如图,在中,分别取AB、AC的中点D、E,连接DE,过点A作 , 垂足为F,将分割后拼接成矩形BCHG,若 , , 则的面积是( )
A、3和4之间 B、4和5之间 C、5和6之间 D、6和7之间7. 如图,在中,分别取AB、AC的中点D、E,连接DE,过点A作 , 垂足为F,将分割后拼接成矩形BCHG,若 , , 则的面积是( )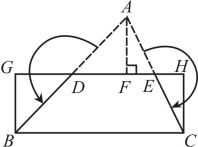 A、8 B、10 C、14 D、168. 我校举行跳绳比赛,甲、乙两班参赛同学每分钟跳绳个数统计结果如下表:
A、8 B、10 C、14 D、168. 我校举行跳绳比赛,甲、乙两班参赛同学每分钟跳绳个数统计结果如下表:班级
参加人数
中位数
方差
平均数
甲
40
129
161
115
乙
40
131
90
115
某同学分析上表后得到如下结论:
①甲、乙两班学生平均成绩相同;
②乙班优秀的人数多于甲班优秀的人数(每分跳绳个数为优秀);
③甲班成绩的波动比乙班大.
上述结论正确的是( )
A、①②③ B、①② C、①③ D、②③二、填空题
-
9. 若在实数范围内有意义,则x的取值范围为 .10. 如图,在四边形ABCD中,对角线AC、BD交于点O,AD∥BC,请添加一个条件: , 使四边形ABCD为平行四边形(不添加任何辅助线).
 11. 两直角边分别为6和8的直角三角形,斜边上的中线的长是 .12.
11. 两直角边分别为6和8的直角三角形,斜边上的中线的长是 .12.如图,在正方形ABCD的外侧,作等边△ADE,则∠AEB= .
 13. 如图,将两条宽度都为3的纸条重叠在一起,使∠ABC=60°,则四边形ABCD的面积为 .
13. 如图,将两条宽度都为3的纸条重叠在一起,使∠ABC=60°,则四边形ABCD的面积为 .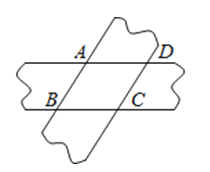 14. 《九章算术》中记载:今有立木,系索其末,委地三尺,引索却行,去本八尺而索尽.问索长几何.译文:今有一竖直着的木柱,在木柱的上端系有绳索,绳索从木柱的上端顺木柱下垂后堆在地面的部分有三尺(绳索比木柱长尺),牵着绳索退行,在距木柱底部尺处时而绳索用尽.设绳索长为尺,则根据题意可列方程为 .
14. 《九章算术》中记载:今有立木,系索其末,委地三尺,引索却行,去本八尺而索尽.问索长几何.译文:今有一竖直着的木柱,在木柱的上端系有绳索,绳索从木柱的上端顺木柱下垂后堆在地面的部分有三尺(绳索比木柱长尺),牵着绳索退行,在距木柱底部尺处时而绳索用尽.设绳索长为尺,则根据题意可列方程为 . 15. 如图,菱形 的边长为4, ,分别以点 和点 为圆心,大于 的长为半径作弧,两弧相交于 两点,直线 交 于点 ,连接 ,则 的长为.
15. 如图,菱形 的边长为4, ,分别以点 和点 为圆心,大于 的长为半径作弧,两弧相交于 两点,直线 交 于点 ,连接 ,则 的长为. 16. 在▱ABCD中,O为AC的中点,点E,M为▱ABCD同一边上任意两个不重合的动点(不与端点重合),EO,MO的延长线分别与▱ABCD的另一边交于点F,N.
16. 在▱ABCD中,O为AC的中点,点E,M为▱ABCD同一边上任意两个不重合的动点(不与端点重合),EO,MO的延长线分别与▱ABCD的另一边交于点F,N.下面四个推断:
①四边形ABFM是平行四边形;
②四边形ENFM是平行四边形;
③若▱ABCD是矩形(正方形除外),则至少存在一个四边形ENFM是正方形;
④对于任意的▱ABCD,存在无数个四边形ENFM是矩形.
其中,正确的有 .
三、解答题
-
17. 计算:18. 如图,在中, , , , , F为AD的中点,求AC,CF的长.
 19. 已知20. 如图,四边形ABCD和四边形AECF都是平行四边形,求证: .
19. 已知20. 如图,四边形ABCD和四边形AECF都是平行四边形,求证: .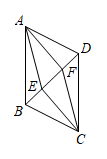 21. 尺规作图:如图,已知线段a,b.
21. 尺规作图:如图,已知线段a,b.
求作:菱形ABCD,使其一条对角线的长等于线段a的长,边长等于线段b的长.
作法:①作直线m,在m上截取线段;
②作线段AC的垂直平分线EF,交线段AC于点O;
③以点A为圆心,线段b的长为半径画弧,交直线EF于点B,D;
④分别连接AB,BC,CD,DA;
则四边形ABCD就是所求作的菱形.
(1)、使用直尺和圆规,依作法补全图形(保留作图痕迹); (2)、完成下面的证明.
(2)、完成下面的证明.证明:∵EF垂直平分AC,
∴AB= ▲ , ▲ = ▲ , ( )
∵ ,
,
∴四边形ABCD是菱形.( )
22. 从2020年5月1日开始,新版《北京市生活垃圾管理条例》正式实施.为了调查同学们对垃圾分类知识的了解情况,小清从我校初中三个年级各随机抽取10人,进行了相关测试,获得了他们的成绩(单位:分),并对成绩进行了整理、描述和分析,下面给出了相关信息:a.30名同学测试成绩的统计图如下:

b.30名同学测试成绩的频数分布直方图如下(数据分成6组: , , , , , ):
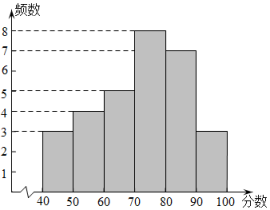
c.测试成绩在这一组的分别是:
73 74 77 75 70 74 73 78
d.小华的知识测试成绩为85分.
根据以上信息,回答下列问题:
(1)、小华的测试成绩在抽取的30名同学的成绩中从高到低排名第 ;(2)、抽取的30名同学的成绩的中位数为;(3)、序号为1-10的学生是七年级的,他们的成绩的方差记为;序号为11-20的学生是八年级的,他们的成绩的方差记为 , 序号为21-30的学生是九年级的,他们的成绩的方差记为 , 直接写出 , , 的大小关系;(4)、成绩80分及以上记为优秀,若我校初中三个年级840名同学都参加测试,估计成绩优秀的同学约为人.23. 如图,在平行四边形中, , 作 , CE交AB于点O,交DA的延长线于点E,连接BE. (1)、求证:四边形ACBE是矩形;(2)、连接OD.若 , , 求OD的长.24. 观察猜想(1)、观察猜想:①;②;③ .
(1)、求证:四边形ACBE是矩形;(2)、连接OD.若 , , 求OD的长.24. 观察猜想(1)、观察猜想:①;②;③ .通过上面三个计算,可以初步对任意的非负实数a,b做出猜想: ;
(2)、验证结论:我们知道可以利用几何图形对一个等式进行验证,请你利用与下图全等的四个矩形,构造几何图形对你的猜想进行验证.(要求:画出构造的图形,写出验证过程) (3)、结论应用:如图,某同学在做一个面积为800cm2 , 对角线相互垂直的四边形玩具时,用来做对角线的竹条至少要m.
(3)、结论应用:如图,某同学在做一个面积为800cm2 , 对角线相互垂直的四边形玩具时,用来做对角线的竹条至少要m. 25. 如图,在正方形ABCD外有一点P,满足 , 以AP,AD为邻边作 .
25. 如图,在正方形ABCD外有一点P,满足 , 以AP,AD为邻边作 . (1)、如图1,根据题目要求补全图形;(2)、连接QC,求的度数;(3)、连接AQ,猜线段AQ,PQ和PB之间的数量关系并证明.26. 在正方形网格中,每个小正方形的边长为1.线段(m,n均为正整数),点A,C在格点上,以AC为对角线画出正方形ABCD(B,D落在网格内).(1)、当m= , n= 时(给出一组值即可),B,D在格点上,在网格中画出正方形ABCD;
(1)、如图1,根据题目要求补全图形;(2)、连接QC,求的度数;(3)、连接AQ,猜线段AQ,PQ和PB之间的数量关系并证明.26. 在正方形网格中,每个小正方形的边长为1.线段(m,n均为正整数),点A,C在格点上,以AC为对角线画出正方形ABCD(B,D落在网格内).(1)、当m= , n= 时(给出一组值即可),B,D在格点上,在网格中画出正方形ABCD; (2)、当m= , n= 时(给出一组值即可),B,D均不在格点上,在网格中画出正方形ABCD(尺规作图,保留痕迹,不写作法);
(2)、当m= , n= 时(给出一组值即可),B,D均不在格点上,在网格中画出正方形ABCD(尺规作图,保留痕迹,不写作法); (3)、当m,n满足时,B,D一定在格点上(网格纸足够用).27. 对于平面直角坐标系xOy中的图形和图形给出如下定义:在图形上存在两点A,B(点A,B可以重合),在图形上存在两点M,N(点M,N可以重合)使得 . 则称图形和图形满足限距关系.(1)、如图,点 , , , 点F在CE上运动(点F可以与C,E重合),连接OF,DF.
(3)、当m,n满足时,B,D一定在格点上(网格纸足够用).27. 对于平面直角坐标系xOy中的图形和图形给出如下定义:在图形上存在两点A,B(点A,B可以重合),在图形上存在两点M,N(点M,N可以重合)使得 . 则称图形和图形满足限距关系.(1)、如图,点 , , , 点F在CE上运动(点F可以与C,E重合),连接OF,DF.①线段OF的最小值为 , 最大值为;线段DF的取值范围是;
②在点O,D中,点与线段CE满足限距关系;
 (2)、如图,正方形ABMN的边长为2,直线PQ分别于x轴,y轴交于点Q,P,且与x轴正方向的夹角始终是 , 若线段PQ与正方形ABMN满足限距关系,求点P的纵坐标的取值范围;
(2)、如图,正方形ABMN的边长为2,直线PQ分别于x轴,y轴交于点Q,P,且与x轴正方向的夹角始终是 , 若线段PQ与正方形ABMN满足限距关系,求点P的纵坐标的取值范围; (3)、如图,正方形ABMN的顶点均在坐标轴上, , G,H是正方形边上两点,分别以G,H为中心作边长为1的正方形,与正方形ABMN的四边分别平行,若对于任意的点G,H,以G,H为中心的正方形都满足限距关系,直接写出b的取值范围.
(3)、如图,正方形ABMN的顶点均在坐标轴上, , G,H是正方形边上两点,分别以G,H为中心作边长为1的正方形,与正方形ABMN的四边分别平行,若对于任意的点G,H,以G,H为中心的正方形都满足限距关系,直接写出b的取值范围.