山东省青岛市胶州市2022年九年级数学一模试题

试卷更新日期：2022-05-26 类型：中考模拟

进入出卷网下载

一、单选题

1. $\frac{\sqrt{3}}{3}$ 的相反数是（）

A、 $\frac{\sqrt{3}}{3}$ B、 $- \frac{\sqrt{3}}{3}$ C、 $\sqrt{3}$ D、 $- \sqrt{3}$

查看试题解析
2. 2022年3月5日，第十三届全国人大五次会议在北京召开，李克强总理代表国务院作《政府工作报告》，报告中指出，2021年我国经济保持恢复发展，国内生产总值达到114万亿元.114万亿＝114000000000000，将数据114000000000000用科学记数法表示为（）

A、 $1.14 \times 1 0^{14}$ B、 $1.14 \times 1 0^{12}$ C、 $0.114 \times 1 0^{14}$ D、 $114 \times 1 0^{12}$

查看试题解析
3. 班徽是班级文化的一种，是整个班级精神的提炼，是班级活力和荣耀的象征．以下四个班徽图案为轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
4. 计算 $2 a b^{2} \cdot (- 3 a^{4} b)^{2}$ 的结果为（）

A、 $12 a^{9} b^{4}$ B、 $- 12 a^{7} b^{4}$ C、 $18 a^{9} b^{4}$ D、 $18 a^{7} b^{4}$

查看试题解析
5. 如图， $A B$ 是 $⊙ O$ 的直径， $C$ ， $D$ 是 $⊙ O$ 上的两点．若 $∠ A O C = 40 °$ ，则 $∠ C D B$ 的度数是（）

A、 $100 °$ B、 $110 °$ C、 $140 °$ D、 $160 °$

查看试题解析
6. 如图，将 $Δ A B C$ 先向下平移1个单位，再绕点 $P$ 按顺时针方向旋转一定角度，得到 $Δ A_{1} B_{1} C_{1}$ ，顶点 $A$ 落到了点 $A_{1} (5 ， 3)$ 处，则点 $B$ 的对应点 $B_{1}$ 的坐标是（）

A、 $(3 ， 0)$ B、 $(3 ， 2)$ C、 $(2 ， 2)$ D、 $(1 ， 2)$

查看试题解析
7. 如图，在 $Δ A B C$ 中， $∠ A = 40 °$ ， $∠ C = 60 °$ ， $D$ 为 $A C$ 边上一点， $D E ⊥ B C$ 于点 $E$ ．若 $A D = B D$ ， $B E = 2$ ，则 $A B$ 的长为（）

A、 $\sqrt{3}$ B、2 C、 $2 \sqrt{3}$ D、4

查看试题解析
8. 若二次函数 $y = a x^{2} + b x + c (a \neq 0)$ 满足 $a - b + c = 0$ ．下列四个结论，其中正确的是（）

A、若二次函数图象经过点 $(3 ， 0)$ ，则 $b = 2 a$ ； B、若 $a = c$ ，则方程 $a x^{2} + b x + c = 0$ 的根为 $x_{1} = x_{2} = - 1$ ； C、二次函数图象与 $x$ 轴一定有两个交点； D、点 $A (x_{1} ， y_{1})$ ， $B (x_{2} ， y_{2})$ 在函数图象上，若 $a > c > 0$ ，则当 $x_{1} < x_{2} < - 1$ 时， $y_{1} < y_{2}$ ．

查看试题解析

二、填空题

9. 计算： $\frac{\sqrt{6} \times \sqrt{3}}{\sqrt{2}} =$ ．

查看试题解析
10. 为了增强青少年的防毒意识，学校举办了一次“禁毒教育”演讲比赛，某位选手的演讲内容，语言表达，演讲技巧这三项得分分别为92分，85分，90分，若依次按40%，40%，20%的比例确定成绩，则该选手的比赛成绩是分．

查看试题解析
11. 已知某几何体的三视图如图所示，则该几何体的体积为．

查看试题解析
12. 如图，在菱形 $A B C D$ 中， $∠ B A D = 60 °$ ， $B D = 2$ ．以点 $A$ 为圆心， $A B$ 的长为半径画弧 $\overset{⌢}{B D}$ ，则图中阴影部分的面积为．

查看试题解析
13. 如图，点 $A$ ， $B$ 在反比例函数 $y = \frac{k}{x} (k > 0 ， x > 0)$ 的图象上，过点 $B$ 分别作 $x$ 轴和 $y$ 轴的垂线，垂足分别为 $C$ ， $D$ ，过点 $A$ 作 $A E$ 垂直于 $x$ 轴，垂足为 $E$ ．若 $O D = 4$ ， $O E = \frac{2}{3} O C$ ，则 $A E =$ ．

查看试题解析
14. 如图，正方形 $A B C D$ 的边长为6，点 $E$ ， $F$ 分别为边 $B C$ ， $C D$ 上两点， $C F = B E$ ， $A E$ 平分 $∠ B A C$ ，连接 $B F$ ，分别交 $A E$ ， $A C$ 于点 $G$ ， $M$ ，点 $P$ 是线段 $A G$ 上的一个动点，过点 $P$ 作 $P N ⊥ A C$ ，垂足为 $N$ ，连接 $P M$ ，则 $P M + P N$ 的最小值为．

查看试题解析

三、解答题

15. 已知： $Δ A B C$ 及 $B C$ 边上一点 $D$ ．
求作： $⊙ O$ ，使 $⊙ O$ 与边 $B C$ 相切，点 $D$ 为切点，且圆心 $O$ 到 $∠ B A C$ 两边的距离相等．

查看试题解析
16.

(1)、化简： $(\frac{1}{a - 1} - \frac{2}{1 - a^{2}}) \cdot \frac{a + 1}{a + 3}$ ；

(2)、解不等式组： ${\begin{array}{l} 3 x \geq 2 x - 1 \\ \frac{x}{2} - 1 < \frac{1}{2} \end{array}$ ，并写出它的正整数解．

查看试题解析
17. 一个不透明的箱子里装有1个红球和若干个白球，这些球除颜色外都相同，将球搅拌均匀后，从中随机摸出一个球，记下颜色后再放回箱子里，不断重复这一过程，发现摸到白球的频率稳定于0.75左右．

(1)、请你估计箱子里白球的个数；

(2)、现从该箱子里随机摸出1个球，记下颜色后放回箱子里，将球搅拌均匀后，再从中随机摸出1个球，求两次摸出的球颜色相同的概率（用画树状图或列表的方法）．

查看试题解析
18. 一架无人机沿水平方向飞行进行测绘工作，在点 $P$ 处测得正前方水平地面上某建筑物 $A B$ 的顶端 $A$ 的俯角为 $24 °$ ．无人机保持飞行方向不变，继续飞行48米到达点 $Q$ 处，此时测得该建筑物底端 $B$ 的俯角为 $66 °$ ．已知建筑物 $A B$ 的高度为36米，求无人机飞行时距离地面的高度．（参考数据： $s i n 2 4^{∘} \approx \frac{2}{5}$ ， $c o s 2 4^{°} \approx \frac{9}{10}$ ， $t a n 2 4^{°} \approx \frac{9}{20}$ ， $s i n 6 6^{°} \approx \frac{9}{10}$ ， $c o s 6 6^{°} \approx \frac{2}{5}$ ， $t a n 6 6^{°} \approx \frac{9}{4}$ ）

查看试题解析
19. 随着北京冬奥会的成功举办，越来越多的人喜欢上冰雪运动，小明对当地 $A$ ， $B$ 两个滑场某一周的日接待游客数进行了统计．数据如下：
请根据以上信息，回答下列问题：

(1)、写出表格中 $a$ ， $b$ ， $c$ ， $d$ 的值；
滑雪场
平均数（千人）
中位数（千人）
众数（千人）
方差
$A$
$a$
1.8
$c$
$d$
$B$
1.8
$b$
1.9
$\frac{29}{350}$

(2)、哪个滑雪场日接待游客数比较稳定？请简要说明理由．

查看试题解析
20. 某综合实践活动小组设计了一个简易电子体重秤，已知装有踏板（踏板质量忽略不计）的可变电阻 $R_{1}$ 与踏板上人的质量 $m$ 之间满足一次函数关系，共图象如图1所示；图2的电路中，电源电压恒为3伏，定值电阻 $R_{0}$ 的阻值为40欧，接通开关，人站上踏板，电压表显示的读数为 $U_{0}$ ，然后把 $U_{0}$ 代入相应的关系式，该读数就可以换算为人的质量 $m$ ，
知识小链接：①导体两端的电压 $U$ ，导体的电阻 $R$ ，通过导体的电流 $I$ ，满足关系式 $I = \frac{U}{R}$ ；②串联电路中电流处处相等，各电阻两端的电压之和等于总电压．

(1)、求可变电阻 $R_{1}$ 与人的质量 $m$ 之间的函数关系；

(2)、用含 $U_{0}$ 的代数式表示 $m$ ；

(3)、当电压表显示的读数 $U_{0}$ 为0.75伏时，求人的质量 $m$ ．

查看试题解析
21. 如图，在 $R t Δ A B C$ 中， $∠ A C B = 90 °$ ，点 $O$ 为 $B C$ 的中点，点 $E$ 为 $A B$ 上一点，过点 $C$ 作 $C D ∥ A B$ 交 $E O$ 的延长线于点 $D$ ，连接 $C E$ ， $B D$ ．

(1)、求证： $Δ C O D ≌ Δ B O E$ ；

(2)、当 $A E = C E$ 时，四边形 $C E B D$ 是什么特殊四边形？请说明理由．

查看试题解析
22. 如图1是一座抛物线型拱桥，图2是其在直角坐标系中的侧面示意图．在正常水位时水面宽 $A B = 24 m$ ，此时水面离桥拱顶部的距离为 $6 m$ ．

(1)、按如图2所示的直角坐标系，求此抛物线的函数表达式；

(2)、如图3，因某种需要，在桥拱顶部及桥的两端树立了三根支柱 $O E$ ， $A C$ ， $B D$ 架设钢缆，在钢缆和桥面之间竖直悬挂若干安全绳，过相邻支柱顶端的钢缆具有相同的抛物线形状，且左、右两条抛物线关于 $y$ 轴对称，左面钢缆抛物线可以用 $y = \frac{1}{12} x^{2} + x + 4$ 表示．
①求左、右面两条钢缆的最低点之间的距离是多少？
②求安全绳长度（钢缆和桥面之间距离）的最小值是多少？

查看试题解析
23. 问题提出：
将一根长度是 $l c m$ （ $l \geq 4$ 的偶数）的细绳按照如图所示的方法对折 $n$ 次（ $n \geq 1$ ），然后从重叠的细绳的一端开始，每隔1厘米（两端弯曲部分的绳长忽略不计）剪1刀，共剪 $m$ 刀（ $m \geq 1$ 的整数），最后得到一些长 $1 c m$ 和长 $2 c m$ 的细绳．如果长 $1 c m$ 的细绳有222根，那么原来的细绳的长度 $l$ 是多少 $c m$ ？
问题探究：
为了解决问题，我们可以先从最简单的情形入手，再逐次递进，从中找出解决问题的方法．
探究一：
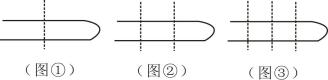
对折1次，可以看成有 $2^{1}$ 根绳子重叠在一起，如果剪1刀（如图①），左端出现了2根长 $1 c m$ 的细绳，右端出现了 $2^{1} - 1 = 1$ 根长 $2 c m$ 的细绳，所以原绳长为 $2 \times 1 + 1 \times 2 = 4 c m$ ；如果剪2刀（如图②），左端仍有2根长 $1 c m$ 的细绳，中间有 $1 \times 2^{1} = 2$ 根长 $1 c m$ 的细绳，右端仍有 $2^{1} - 1 = 1$ 根长 $2 c m$ 的细绳，所以原绳长为 $(2 + 2) \times 1 + 1 \times 2 = 6 c m$ ；如果剪3刀（如图③），左端仍有2根长 $1 c m$ 的细绳，中间有 $2 \times 2^{1} = 4$ 根长 $1 c m$ 的细绳，右端仍有 $2^{1} - 1 = 1$ 根长 $2 c m$ 的细绳，所以原绳长为 $(2 + 4) \times 1 + 1 \times 2 = 8 c m$ ；以此类推，如果剪 $m$ 刀，左端仍有2根长 $1 c m$ 的细绳，中间有 $(m - 1) \times 2^{1} = 2 (m - 1)$ 根长 $1 c m$ 细绳，右端仍有 $2^{1} - 1 = 1$ 根长 $2 c m$ 的细绳，所以，原绳长为 $[2 + (m - 1) \times 2^{1}] \times 1 + (2^{1} - 1) \times 2 = (2 m + 2) = 2 (m + 1) c m$ ．
探究二：
对折2次，可以看成有 $2^{2}$ 根绳子重叠在一起，如果剪1刀（如图④），左端出现了2根长 $1 c m$ 的细绳，两端共出现了 $2^{2} - 1 = 3$ 根长 $2 c m$ 的细绳，所以原绳长为 $2 \times 1 + 3 \times 2 = 8 c m$ ；如果剪2刀（如图⑤），左端仍有2根长 $1 c m$ 的细绳，中间有 $1 \times 2^{2} = 4$ 根长 $1 c m$ 的细绳，两端仍有 $2^{2} - 1 = 3$ 根长 $2 c m$ 的细绳，所以原绳长为 $(2 + 4) \times 1 + 3 \times 2 = 12 c m$ ；如果剪3刀（如图⑥），左端仍有2根长 $1 c m$ 的细绳，中间有 $2 \times 2^{2} = 8$ 根长 $1 c m$ 的细绳，两端共有 $2^{2} - 1 = 3$ 根长 $2 c m$ 的细绳，所以原绳长为 $(2 + 8) \times 1 + 3 \times 2 = 16 c m$ ；以此类推，如果剪 $m$ 刀，左端仍有2根长 $1 c m$ 的细绳，中间有 $(m - 1) \times 2^{2} = (4 m - 4) = 4 (m - 1)$ 根长 $1 c m$ 的细绳，两端仍有 $2^{2} - 1 = 3$ 根长 $2 c m$ 的细绳，所以原绳长为 $[2 + (m - 1) \times 2^{2}] \times 1 + 3 \times 2 = (4 m + 4) = 4 (m + 1) c m$ ．
探究三：
对折3次（如图⑦），可以看成有 $2^{3}$ 根绳子重叠在一起，如果剪 $m$ 刀，左端有2根长 $1 c m$ 的细绳，中间有 $(m - 1) \times 2^{3} = (8 m - 8) = 8 (m - 1)$ 根长 $1 c m$ 的细绳，两端有 $2^{3} - 1 = 7$ 根长 $2 c m$ 的细绳，所以原绳长为 $[2 + (m - 1) \times 2^{3}] \times 1 + 7 \times 2 = (8 m + 8) = 8 (m + 1)$ cm．

(1)、总结规律：
对折 $n$ 次，可以看成有根绳子重叠在一起，如果剪 $m$ 刀，左端有根长 $1 c m$ 的细绳，中间会有根长 $1 c m$ 的细绳，两端会有根长 $2 c m$ 的细绳，所以原绳长为 $c m$ ．

(2)、问题解决：
如果长 $1 c m$ 的细绳有222根，根据以上探究过程可以推算出细绳可能被对折了次，被剪了刀，原来的细绳的长度 $l$ 是 $c m$ ．

(3)、拓展应用：
如果长 $1 c m$ 的细绳有2024根，那么原来的细绳的长度 $l$ 是 $c m$ ．

查看试题解析
24. 如图，在 $R t Δ A B C$ 中， $∠ B A C = 90 °$ ， $A B = 6 c m$ ， $B C = 10 c m$ ，在 $B C$ 上取一点 $D$ ，使 $B D = A B = 6 c m$ ，连接 $A D$ ，分别过点 $A$ ，点 $C$ ，作 $A E ∥ B C$ ， $C E ∥ A D$ ，交点为 $E$ ．点 $P$ 从点 $A$ 出发，沿 $A C$ 方向匀速运动，速度为 $1 c m / s$ ；同时，点 $Q$ 从点 $B$ 出发，沿 $B A$ 方向匀速运动，速度为 $1 c m / s$ ．过点 $P$ 作 $P F ∥ C E$ ，交 $A E$ 于点 $F$ ，连接 $P D$ ， $D Q$ ．设运动时间为 $t (s) (0 < t < 6)$ ，解答下列问题：

(1)、当 $t$ 为何值时，点 $P D ∥ A B$ ？

(2)、设五边形 $A F P D Q$ 的面积为 $S (c m^{2})$ ，求 $S$ 与 $t$ 之间的函数关系式；

(3)、在运动过程中，是否存在某一时刻 $t$ ，使 $S_{五边形 A F P D Q} ： S_{四边形 A B C E} = 5 ： 14$ ？若存在，求出 $t$ 的值；若不存在，请说明理由；

(4)、连接 $B P$ ，是否存在某一时刻 $t$ ，使得 $P B$ 垂直平分 $A D$ ？若存在，求出 $t$ 的值；若不存在，请说明理由．

查看试题解析

滑雪场	平均数（千人）	中位数（千人）	众数（千人）	方差
$A$	$a$	1.8	$c$	$d$
$B$	1.8	$b$	1.9	$\frac{29}{350}$