山东省临沂市平邑县2022年九年级一模数学试题
试卷更新日期:2022-05-26 类型:中考模拟
一、单选题
-
1. 据国家卫健委网站消息,截至2022年4月10日,31个省(自治区、直辖市)和新疆生产建设兵团累计报告接种新冠病毒疫苗超33亿剂次.33亿用科学记数法表示为( )A、 B、 C、 D、
-
2. 下面是一位同学做的四道题:
①2a+3b=5ab;②﹣(﹣2a2b3)4=﹣16a8b12;③(a+b)3=a3+b3;④(a﹣2b)2=a2﹣2ab+4b2其中做对的一道题的序号是( )
A、① B、② C、③ D、④ -
3. 如图1是用5个相同的正方体搭成的立体图形,若由图1变化至图2,则三视图中没有发生变化的是( )
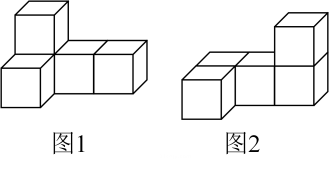 A、主视图 B、主视图和左视图 C、主视图和俯视图 D、左视图和俯视图
A、主视图 B、主视图和左视图 C、主视图和俯视图 D、左视图和俯视图 -
4. 如图, , ,垂足为B , ,则 的度数为( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
5. 如图,在△ABC中,AB=5,AC=4,BC=3,分别以点A,点B为圆心,大于 AB的长为半径画弧,两弧相交于点M,N,作直线MN交AB于点O,连接CO,则CO的长是( )
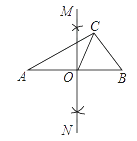 A、1.5 B、2 C、2.4 D、2.5
A、1.5 B、2 C、2.4 D、2.5 -
6. 如图所示的网格是正方形网格,A,B,C,D是网格线交点,则与的大小关系为( )
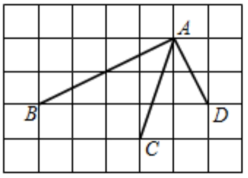 A、 B、 C、 D、无法确定
A、 B、 C、 D、无法确定 -
7. 以方程组的解为坐标,点在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限
-
8. 关于的一元二次方程 , 下列结论错误的是( )A、当方程有实数根时 B、当时,方程一定有两个不相等的实数根 C、当时,方程的实数根为 , D、若 , 为方程的两个实数根,则有
-
9. 小明准备画一个二次函数的图象,他首先列表(如下),但在填写函数值时,不小心把其中一个蘸上了墨水(表中
 ),那么这个被蘸上了墨水的函数值是( )
),那么这个被蘸上了墨水的函数值是( )x
…
-1
0
1
2
3
…
y
…

3
4
3
0
…
A、-1 B、3 C、4 D、0 -
10. 在平面直角坐标系 中,若函数图象上任意两点 , 均满足 .下列四个函数图象中,
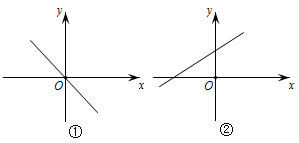
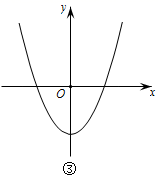
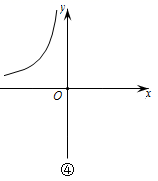
所有正确的函数图象的序号是( )
A、①② B、③④ C、①③ D、②④ -
11. 如图,在平行四边形 中, , ,过点 作边 的垂线 交 的延长线于点 ,点 是垂足,连接 、 , 交 于点 .则下列结论:①四边形 是正方形;② ;③ ;④ ,正确的个数是( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
12. 小云计划户外徒步锻炼,每天有“低强度”“高强度”“休息”三种方案,下表对应了每天不同方案的徒步距离(单位:km).若选择“高强度”要求前一天必须“休息”(第一天可选择“高强度”).则小云5天户外徒步锻炼的最远距离为( )km.
日期
第1天
第2天
第3天
第4天
第5天
低强度
8
6
6
5
4
高强度
12
13
15
12
8
休息
0
0
0
0
0
A、35 B、36 C、37 D、38
二、填空题
-
13. 已知x和y满足方程组 , 则代数式的值为 .
-
14. 用四个不等式①a>b,②a +b>2b,③a>0,④a2>ab中的两个不等式作为题设,余下的两个不等式中选择一个作为结论,组成一个真命题: .
-
15. 规定:在平面内,如果一个图形绕一个定点旋转一定的角度后能与自身重合,那么就称这个图形是旋转对称图形,转动的这个角度称为这个图形的一个旋转角.例如:正方形绕着两条对角线的交点O旋转90°或180°后,能与自身重合(如图),所以正方形是旋转对称图形,且有两个旋转角.
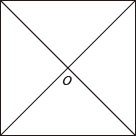
根据以上规定,下列图形是旋转对称图形,也是中心对称图形的是 .
①正五边形;②正六边形;③矩形;④菱形
-
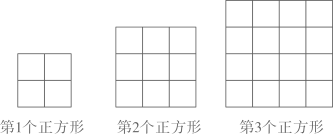
16. 如图,用大小相同的小正方形拼大正方形,拼第1个正方形需要4个小正方形,拼第2个正方形需要9个小正方形……,按这样的方法拼成的第 个正方形比第n个正方形多个小正方形.
三、解答题
-
17. 计算: .
-
18. 某校初三(1)班部分同学接受一次内容为“最适合自己的考前减压方式”的调查活动,收集整理数据后,老师将减压方式分为五类,并绘制了图1、图2两个不完整的统计图,请根据图中的信息解答下列问题.
 (1)、初三(1)班接受调查的同学共有多少名;(2)、补全条形统计图,并计算扇形统计图中的“体育活动C”所对应的圆心角度数;(3)、若喜欢“交流谈心”的5名同学中有三名男生和两名女生;老师想从5名同学中任选两名同学进行交流,直接写出选取的两名同学都是女生的概率.
(1)、初三(1)班接受调查的同学共有多少名;(2)、补全条形统计图,并计算扇形统计图中的“体育活动C”所对应的圆心角度数;(3)、若喜欢“交流谈心”的5名同学中有三名男生和两名女生;老师想从5名同学中任选两名同学进行交流,直接写出选取的两名同学都是女生的概率. -
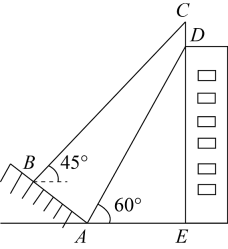
19. 如图,某建筑物的顶部有一块标识牌CD,小明在斜坡上B处测得标识牌顶部C的仰角为45°,沿斜坡走下来在地面A处测得标识牌底部D的仰角为60°,已知斜坡AB的坡角为30°,米.求标识牌CD的高.
-
20. 如图,AB为⊙O直径,C、D为⊙O上不同于A、B的两点,∠ABD=2∠BAC,连接CD.过点C作CE⊥DB,垂足为E,直线AB与CE相交于F点.
 (1)、求证:CF为⊙O的切线;(2)、当BF=5,sinF= 时,求BD的长.
(1)、求证:CF为⊙O的切线;(2)、当BF=5,sinF= 时,求BD的长. -
21. 在初中阶段的函数学习中,我们经历了列表,描点,连线画函数图象,并结合图象研究函数性质的过程.若一个函数当自变量在不同范围内取值时,函数表达式不同,我们称这样的函数为分段函数.下面我们参照函数学习的过程与方法,探究分段函数的图象与性质,探究过程如下,请补充完整,(1)、列表:
x
…
-6
-5
-4
-3
-2
-1
0
1
2
3
…
y
…
m
1
n
1
2
3
4
…
其中, , .
(2)、描点:在平面直角坐标系中,以自变量x的取值为横坐标,以相应的函数值y为纵坐标,描出相应的点,如图所示,请画出函数的图象.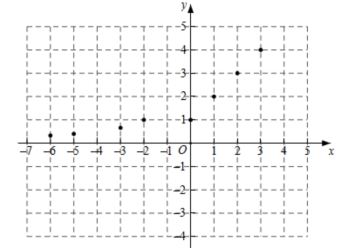 (3)、研究函数并结合图象与表格,回答下列问题:
(3)、研究函数并结合图象与表格,回答下列问题:①点 , , , 在函数图象上,则 ▲ , ▲ ;(填“>”,“=”或“<”);
②直线与图象相交,交点依次从左到右为M,N,K三点,如果 , 求t的值.
-
22. 受新冠肺炎疫情影响,一水果种植专业户有大量成熟水果无法出售.“一方有难,八方支援”,某水果经销商主动从该种植专业户购进甲、乙两种水果进行销售.专业户为了感谢经销商的援助,对甲种水果的出售价格根据购买量给予优惠,对乙种水果按25元/千克的价格出售.设经销商购进甲种水果 千克,付款 元, 与 之间的函数关系如图所示.
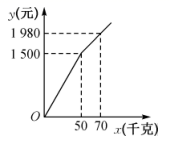 (1)、直接写出当 和 时, 与 之间的函数表达式;(2)、若经销商计划一次性购进甲、乙两种水果共100千克,且甲种水果不少于40千克,但又不超过60千克.如何分配甲、乙两种水果的购进量,才能使经销商付款总金额 (元)最少?
(1)、直接写出当 和 时, 与 之间的函数表达式;(2)、若经销商计划一次性购进甲、乙两种水果共100千克,且甲种水果不少于40千克,但又不超过60千克.如何分配甲、乙两种水果的购进量,才能使经销商付款总金额 (元)最少? -
23. 在正方形ABCD中,点E在射线BC上(不与点B、C重合),连接DB,DE,将DE绕点E逆时针旋转90°得到EF,连接BF.
 (1)、如图1,点E在BC边上.
(1)、如图1,点E在BC边上.①依题意补全图1;
②若AB=6,EC=2,求BF的长;
(2)、如图2,点E在BC边的延长线上,用等式表示线段BD,BE,BF之间的数量关系.
