山东省临沂市莒南县2022年中考一模数学试题
试卷更新日期:2022-05-26 类型:中考模拟
一、单选题
-
1. 在实数、、、中,相反数最小的是( ).A、 B、 C、 D、2. 下列设计的图案中,是中心对称图形但不是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 2021年政府工作报告指出,过去五年来,我国经济实力跃上新台阶.国内生产总值从8.32万亿元增加到11.4亿亿元,稳居世界第二,11.4亿亿用科学记数法表示为( ).A、 B、 C、 D、4. 下列正确的个数是( ).
3. 2021年政府工作报告指出,过去五年来,我国经济实力跃上新台阶.国内生产总值从8.32万亿元增加到11.4亿亿元,稳居世界第二,11.4亿亿用科学记数法表示为( ).A、 B、 C、 D、4. 下列正确的个数是( ).①;②;
③;④;
⑤;⑥ .
A、1个 B、2个 C、3个 D、4个5. 点O,A,B,C在数轴上的位置如图所示,O为原点,AC=1,OA=OB.若点C所表示的数为a,则点B所表示的数为( ). A、﹣a-1 B、﹣a+1 C、a+1 D、a﹣16. 在2019年世界军人运动会中,我国军人运动员屡创佳绩,特别是在射击赛场获得很多金牌,如图是某项射击项目的射击靶示意图,其中每环的宽度与中心圆的半径相等,某运动员朝靶上任意射击一次没有脱靶,设其命中10、9、8、7的概率分别为、、、 , 则下列选项正确的是( ).
A、﹣a-1 B、﹣a+1 C、a+1 D、a﹣16. 在2019年世界军人运动会中,我国军人运动员屡创佳绩,特别是在射击赛场获得很多金牌,如图是某项射击项目的射击靶示意图,其中每环的宽度与中心圆的半径相等,某运动员朝靶上任意射击一次没有脱靶,设其命中10、9、8、7的概率分别为、、、 , 则下列选项正确的是( ).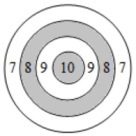 A、 B、 C、 D、7. 若关于x的方程的解为整数解,则满足条件的所有整数a的和是( )A、6 B、0 C、1 D、98. 已知关于的一元二次方程的两个不相等的实数根 , 满足 , 则的值为( )A、-3 B、1 C、-3 或1 D、29. 如图是某几何体的三视图,根据图中的数据,求得该几何体的体积为( )
A、 B、 C、 D、7. 若关于x的方程的解为整数解,则满足条件的所有整数a的和是( )A、6 B、0 C、1 D、98. 已知关于的一元二次方程的两个不相等的实数根 , 满足 , 则的值为( )A、-3 B、1 C、-3 或1 D、29. 如图是某几何体的三视图,根据图中的数据,求得该几何体的体积为( )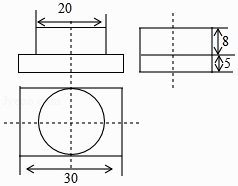 A、800π+1200 B、160π+1700 C、3200π+1200 D、800π+300010. 在中,已知 , , . 如图所示,将绕点A按逆时针方向旋转90°后得到 . 则图中阴影部分面积为( ).
A、800π+1200 B、160π+1700 C、3200π+1200 D、800π+300010. 在中,已知 , , . 如图所示,将绕点A按逆时针方向旋转90°后得到 . 则图中阴影部分面积为( ). A、 B、 C、 D、11. 如图,正方形ABCD的边长为5,点A的坐标为 , 点B在y轴上,若反比例函数的图象过点C,则该反比例函数的表达式为( ).
A、 B、 C、 D、11. 如图,正方形ABCD的边长为5,点A的坐标为 , 点B在y轴上,若反比例函数的图象过点C,则该反比例函数的表达式为( ).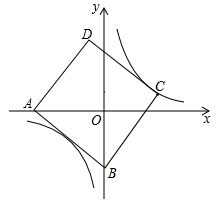 A、 B、 C、 D、12. 如图,四边形 内接于 , 为直径, ,过点 作 于点 ,连接 交 于点 .若 , ,则 的长为( )
A、 B、 C、 D、12. 如图,四边形 内接于 , 为直径, ,过点 作 于点 ,连接 交 于点 .若 , ,则 的长为( )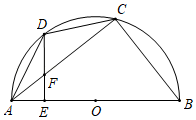 A、8 B、10 C、12 D、16
A、8 B、10 C、12 D、16二、填空题
-
13. 已知 , 那么的值是 .14. 如图,方格纸上每个小正方形的边长均为1个单位长度,点O,A,B,C在格点(两条网格线的交点叫格点)上,以点O为原点建立直角坐标系,则过A,B,C三点的圆的圆心坐标为 .
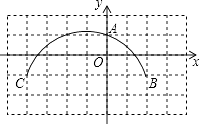 15. 一个长方体木箱沿斜面下滑,当木箱滑至如图位置时, , 已知木箱高 , 斜面坡角为 , 则木箱端点距地面的高度为 .
15. 一个长方体木箱沿斜面下滑,当木箱滑至如图位置时, , 已知木箱高 , 斜面坡角为 , 则木箱端点距地面的高度为 . 16. 阅读理解:如图1,与直线a,b都相切,不论如何转动,直线a,b之间的距离始终保持不变(等于的半径),我们把具有这一特性的图形称为“等宽曲线”.图2是利用圆的这一特性的例子,将等直径的圆棍放在物体下面,通过圆棍滚动,用较小的力就可以推动物体前进.据说,古埃及就是利用这种方法将巨石推到金字塔顶的.
16. 阅读理解:如图1,与直线a,b都相切,不论如何转动,直线a,b之间的距离始终保持不变(等于的半径),我们把具有这一特性的图形称为“等宽曲线”.图2是利用圆的这一特性的例子,将等直径的圆棍放在物体下面,通过圆棍滚动,用较小的力就可以推动物体前进.据说,古埃及就是利用这种方法将巨石推到金字塔顶的.
拓展应用:如图3所示的弧三角形(也称为莱洛三角形)也是“等宽曲线”.如图4,夹在平行线c,d之间的莱洛三角形无论怎么滚动,平行线间的距离始终不变.若直线c,d之间的距离等于4cm,则莱洛三角形的周长为cm.
三、解答题
-
17.(1)、 .(2)、 , 其中a是不等式组的最小整数解.18. 随着信息技术的迅猛发展,人们去商场购物的支付方式更加多样、便捷.某校数学兴趣小组设计了一份调查问卷,要求每人选且只选一种你最喜欢的支付方式.现将调查结果进行统计并绘制成如下两幅不完整的统计图,请结合图中所给的信息解答下列问题:
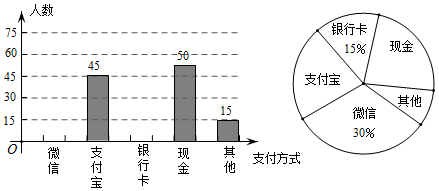 (1)、这次活动共调查了人;在扇形统计图中,表示“支付宝”支付的扇形圆心角的度数为;(2)、将条形统计图补充完整.观察此图,支付方式的“众数”是▲ ”;(3)、在一次购物中,小明和小亮都想从“微信”、“支付宝”、“银行卡”三种支付方式中选一种方式进行支付,请用画树状图或列表格的方法,求出两人恰好选择同一种支付方式的概率.19. 小明根据学习函数的经验,对的图像与性质进行了研究.
(1)、这次活动共调查了人;在扇形统计图中,表示“支付宝”支付的扇形圆心角的度数为;(2)、将条形统计图补充完整.观察此图,支付方式的“众数”是▲ ”;(3)、在一次购物中,小明和小亮都想从“微信”、“支付宝”、“银行卡”三种支付方式中选一种方式进行支付,请用画树状图或列表格的方法,求出两人恰好选择同一种支付方式的概率.19. 小明根据学习函数的经验,对的图像与性质进行了研究.下面是小明的探究过程,请补充完整:
(1)、函数的自变量x的取值范围 .(2)、下表列出y与x的几组对应值,请写出m、n的值,m= , n= .x
…
1
2
3
4
…
y
…
m
2
n
…
(3)、如图,在平面直角坐标系xOy中,指出以上列表中各对对应值为坐标的点,根据描出的点,画出该函数的图象. (4)、结合函数图象,完成:
(4)、结合函数图象,完成:①当时,x= .
②写出该函数的一条性质 .
③若方程有两个不相等的实数根,则t的取值范围是 .
20. 某校九年级某班开展数学活动,小明和小军合作用一副三角板测量学校的旗杆,小明站在B点测得旗杆顶端E点的仰角为45°,小军站在D点测得旗杆顶端E点的仰角为30°.已知小明和小军的距离BD=6 m,小明的身高AB=1.5 m,小军的身高CD=1.75 m,求旗杆的高EF.(结果精确到0.1,参考数据:≈1.41,≈1.73) 21. 如图,抛物线y= x2+bx-2与x轴交于A、B两点, 与y轴交于C点,且A(一1,0).
21. 如图,抛物线y= x2+bx-2与x轴交于A、B两点, 与y轴交于C点,且A(一1,0). (1)、求抛物线的解析式及顶点D的坐标;(2)、判断△ABC的形状,证明你的结论;(3)、点M(m,0)是x轴上的一个动点,当CM+DM的值最小时,求m的值.22. 如图,在Rt△ABC中,∠ACB=90°,AO是△ABC的角平分线.以O为圆心,OC为半径作⊙O.
(1)、求抛物线的解析式及顶点D的坐标;(2)、判断△ABC的形状,证明你的结论;(3)、点M(m,0)是x轴上的一个动点,当CM+DM的值最小时,求m的值.22. 如图,在Rt△ABC中,∠ACB=90°,AO是△ABC的角平分线.以O为圆心,OC为半径作⊙O. (1)、求证:AB是⊙O的切线.
(1)、求证:AB是⊙O的切线.
(2)、已知AO交⊙O于点E,延长AO交⊙O于点D,tanD= ,求 的值.(3)、在(2)的条件下,设⊙O的半径为3,求AB的长.23. 知识再现:已知,如图1,四边形ABCD是正方形,点M、N分别在边BC、CD上,连接AM、AN、MN,且 , 延长CB至G使 , 连接AG,根据三角形全等的知识,我们可以证明 . (1)、知识探究:如图1中,作 , 垂足为点H,猜想AH与AB有什么数量关系?并进行证明.(2)、知识运用:如图2,四边形ABCD是正方形,E是边BC的中点,F为边CD上一点, , , 求DF的长.(3)、知识拓展:已知 , 于点D,且 , , 求CD的长.
(1)、知识探究:如图1中,作 , 垂足为点H,猜想AH与AB有什么数量关系?并进行证明.(2)、知识运用:如图2,四边形ABCD是正方形,E是边BC的中点,F为边CD上一点, , , 求DF的长.(3)、知识拓展:已知 , 于点D,且 , , 求CD的长.