山东省临沂市费县2022年中考数学一模试题
试卷更新日期:2022-05-26 类型:中考模拟
一、单选题
-
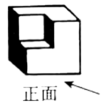
1. =( )A、-2022 B、 C、2022 D、2. 如图所示的几何体的俯视图是( )
 A、
A、 B、
B、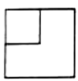 C、
C、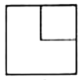 D、
D、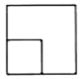 3. 下列计算正确的是( )A、 B、 C、 D、4. 用配方法解方程 时,配方结果正确的是( )A、 B、 C、 D、5. 估计的值应在( )A、4和5之间 B、5和6之间 C、6和7之间 D、7和8之间6. 将一副三角尺如图摆放,点E在 上,点D在 的延长线上, ,则 的度数是( )
3. 下列计算正确的是( )A、 B、 C、 D、4. 用配方法解方程 时,配方结果正确的是( )A、 B、 C、 D、5. 估计的值应在( )A、4和5之间 B、5和6之间 C、6和7之间 D、7和8之间6. 将一副三角尺如图摆放,点E在 上,点D在 的延长线上, ,则 的度数是( )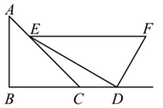 A、15° B、20° C、25° D、30°7. 同时抛掷两枚质地均匀的硬币,则一枚硬币正面向上、一枚硬币反面向上的概率是( )A、 B、 C、 D、8. 化简的结果是( )A、 B、 C、 D、9. 我国古代数学经典著作《九章算术》中有这样一题,原文是:“今有共买物,人出八,盈三;人出七,不足四.问人数、物价各几何?”意思是:今有人合伙购物,每人出八钱,会多三钱;每人出七钱,又差四钱.问人数、物价各多少?设人数为 人,物价为 钱,下列方程组正确的是( )A、 B、 C、 D、10. 抖空竹在我国有着悠久的历史,是国家级的非物质文化遗产之一.如示意图, , 分别与相切于点C,D,延长 , 交于点P.若的半径为 , 则图中弧的长为____ . (结果保留)
A、15° B、20° C、25° D、30°7. 同时抛掷两枚质地均匀的硬币,则一枚硬币正面向上、一枚硬币反面向上的概率是( )A、 B、 C、 D、8. 化简的结果是( )A、 B、 C、 D、9. 我国古代数学经典著作《九章算术》中有这样一题,原文是:“今有共买物,人出八,盈三;人出七,不足四.问人数、物价各几何?”意思是:今有人合伙购物,每人出八钱,会多三钱;每人出七钱,又差四钱.问人数、物价各多少?设人数为 人,物价为 钱,下列方程组正确的是( )A、 B、 C、 D、10. 抖空竹在我国有着悠久的历史,是国家级的非物质文化遗产之一.如示意图, , 分别与相切于点C,D,延长 , 交于点P.若的半径为 , 则图中弧的长为____ . (结果保留)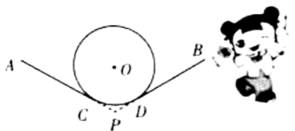 A、 B、 C、 D、11. 如图,在中, , 点O是的三等分点,半圆O与相切,M,N分别是与半圆弧上的动点,则的最小值和最大值之和是( )
A、 B、 C、 D、11. 如图,在中, , 点O是的三等分点,半圆O与相切,M,N分别是与半圆弧上的动点,则的最小值和最大值之和是( ) A、8 B、10 C、12 D、1412. 如图,点A,B在反比例函数的图象上,轴于点C,轴于点D,轴于点E,连结 . 若 , 则k的值为( )
A、8 B、10 C、12 D、1412. 如图,点A,B在反比例函数的图象上,轴于点C,轴于点D,轴于点E,连结 . 若 , 则k的值为( ) A、8 B、9 C、 D、
A、8 B、9 C、 D、二、填空题
-
13. 分解因式:=.14. 分式方程的解为 .15. 如图,在单位长度为1米的平面直角坐标系中,曲线是由半径为2米,圆心角为的多次复制并首尾连接而成.现有一点P从A(A为坐标原点)出发,以每秒米的速度沿曲线向右运动,则在第2022秒时点P的坐标为 .
 16. 如图,正方形中, , 连接的平分线交于点E,在上截取 , 连接 , 分别交于点G,H,点P是线段上的动点,于点Q,连接 . 下列结论:①;②;③;④的最小值是 . 其中所有正确结论的序号是
16. 如图,正方形中, , 连接的平分线交于点E,在上截取 , 连接 , 分别交于点G,H,点P是线段上的动点,于点Q,连接 . 下列结论:①;②;③;④的最小值是 . 其中所有正确结论的序号是
三、解答题
-
17. 解不等式组: ,并写出它的所有整数解.18. 张明是某社区管理员,他在一楼房前点A处垂直升空一无人机巡查小区,当无人机升高到离地面100米的点D处时,以5米每秒的速度沿方向飞行,已知点A观察楼顶C的仰角是 , 问自D点飞行多少秒时无人机刚好离开张明的视线?参考数据:
 19. 为了解我县A,B两个乡镇板材企业第一季度的收入情况,从这两个乡镇的板材企业中,各随机抽取了25家板材企业,获得了它们第一季度收入(单位:百万元)的数据,并对数据进行整理、描述和分析.下面给出了部分信息.
19. 为了解我县A,B两个乡镇板材企业第一季度的收入情况,从这两个乡镇的板材企业中,各随机抽取了25家板材企业,获得了它们第一季度收入(单位:百万元)的数据,并对数据进行整理、描述和分析.下面给出了部分信息.⑴A乡镇板材企业第一季度收入的数据的频数分布直方图如下图(数据分成5组:):

⑵A乡镇板材企业第一季度收入的数据在这一组的是:10.0;10.0;10.1;10.9;11.4;11.5;11.6;11.8
⑶A,B两个乡镇板材企业第一季度收入的数据的平均数、中位数如下:
平均数
中位数
A乡镇
10.8
a
B乡镇
11.0
11.5
根据以上信息,回答下列问题:
①写出表中a的值:
②在A乡镇抽取的板材企业,记第一季度收入高于它们的平均收入的板材企业的个数为m.在B乡镇抽取的板材企业,记第一季度收入高于它们的平均收入的板材企业的个数为n.比较m,n的大小,并说明理由;
③若B乡镇共有100家板材企业,估计B乡镇的板材企业第一季度的总收入(直接写出结果).
20. 如图,为的直径,C为上一点,弦的延长线与过点C的切线互相垂直,垂足为D, , 连接 . (1)、求的度数;(2)、若 , 求的长.21. 为了探索函数的图象与性质,我们参照学习函数的过程与方法,列表:
(1)、求的度数;(2)、若 , 求的长.21. 为了探索函数的图象与性质,我们参照学习函数的过程与方法,列表:x
…
1
2
3
4
5
…
y
…
2
…
描点:在平面直角坐标系中,以自变量x的取值为横坐标,以相应的函数值y为纵坐标,描出相应的点,如图1所示:
 (1)、如图1,观察所描出点的分布,用一条光滑曲线将点顺次连接起来,作出函数图象;(2)、已知点在函数图象上,结合表格和函数图象,回答下列问题:
(1)、如图1,观察所描出点的分布,用一条光滑曲线将点顺次连接起来,作出函数图象;(2)、已知点在函数图象上,结合表格和函数图象,回答下列问题:若 , 则;若 , 则;(填“>”,“=”,“<”).
(3)、某农户积极响应厕所改造工程,要建造一个图2所示的长方体形的化粪池,其底面积为1平方米,深为1米.已知下底面造价为1千元/平方米,上盖的造价为1.5千元/平方米,侧面造价为0.5千元/平方米,设水池底面一边的长为x米,水池总造价为y千元.①请写出y关于x的函数关系式;
②若该农户建造化粪池的预算不超过5千元,则池子底面一边的长x应控制在什么范围内?
22. 定义:若一个函数图象上存在横、纵坐标相等的点,则称该点为这个函数图象的“等值点”,例如,点是函数的图象的“等值点”.(1)、分别判断函数的图象上是否存在“等值点”?如果存在,求出“等值点”的坐标;如果不存在,说明理由;(2)、写出函数的等值点坐标;(3)、若函数的图象记为 , 将其沿直线翻折后的图象记为 . 当两部分组成的图象上恰有2个“等值点”时,请写出m的取值范围.23. 某学习小组开展了图形旋转的探究活动:将一个矩形绕点A顺时针旋转 , 得到矩形 , 连结 . (1)、如图1,当时,点恰好在延长线上.若 , 求的长.(2)、如图2,连结 , 过点作交于点M.观察思考线段与数量关系并说明理由.(3)、在(2)的条件下,射线交于点N(如图3),若 , 旋转角等于多少度时是等边三角形,请写出的值,并说明是等边三角形的理由.
(1)、如图1,当时,点恰好在延长线上.若 , 求的长.(2)、如图2,连结 , 过点作交于点M.观察思考线段与数量关系并说明理由.(3)、在(2)的条件下,射线交于点N(如图3),若 , 旋转角等于多少度时是等边三角形,请写出的值,并说明是等边三角形的理由.