山东省聊城市临清市2022年九年级第二次模拟考试数学试题
试卷更新日期:2022-05-26 类型:中考模拟
一、单选题
-
1. 实数 , 2,0,中,最小的数是( )A、 B、2 C、0 D、2. 几何体的三视图如图所示,这个几何体是( )
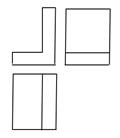 A、
A、 B、
B、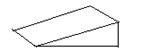 C、
C、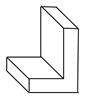 D、
D、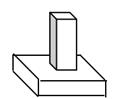 3. 下列调查中,适宜采用抽样调查的是( )A、调查某批次医用口罩的合格率 B、了解某校八年级一班学生的视力情况 C、了解100张百元钞票中有没有假钞 D、调查神舟十四号载人飞船各零部件的质量4. 如图,若AB∥CD,CD∥EF,那么BCE=( )
3. 下列调查中,适宜采用抽样调查的是( )A、调查某批次医用口罩的合格率 B、了解某校八年级一班学生的视力情况 C、了解100张百元钞票中有没有假钞 D、调查神舟十四号载人飞船各零部件的质量4. 如图,若AB∥CD,CD∥EF,那么BCE=( ) A、180°-2+1 B、180°-1-2 C、2=21 D、1+25. 下列运算正确的是( )A、 B、 C、 D、6. 定义 ,则方程 的解为( )A、 B、 C、 D、7. 如表是有关企业和世界卫生组织统计的5种新冠疫苗的有效率,则这5种疫苗有效率的中位数是( )
A、180°-2+1 B、180°-1-2 C、2=21 D、1+25. 下列运算正确的是( )A、 B、 C、 D、6. 定义 ,则方程 的解为( )A、 B、 C、 D、7. 如表是有关企业和世界卫生组织统计的5种新冠疫苗的有效率,则这5种疫苗有效率的中位数是( )疫苗名称
克尔来福
阿斯利康
莫德纳
辉瑞
卫星V
有效率
79%
76%
95%
95%
92%
A、79% B、92% C、95% D、76%8. 如图,中,点C为弦中点,连接 , , , 点D是上任意一点,则度数为( )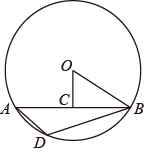 A、 B、 C、 D、9. 已知抛物线()与直线交于 , 两点,则关于的不等式的解集是( )A、或 B、或 C、 D、10. 在设计人体雕像时,使雕像上部(腰部以上)与下部(腰部以下)的高度比,等于下部与全部的高度比,可以增加视觉美感.如图,按此比例设计一座高度为的雷锋雕像,那么该雕像的下部设计高度约是( )(精确到0.01.参考数据: , , )
A、 B、 C、 D、9. 已知抛物线()与直线交于 , 两点,则关于的不等式的解集是( )A、或 B、或 C、 D、10. 在设计人体雕像时,使雕像上部(腰部以上)与下部(腰部以下)的高度比,等于下部与全部的高度比,可以增加视觉美感.如图,按此比例设计一座高度为的雷锋雕像,那么该雕像的下部设计高度约是( )(精确到0.01.参考数据: , , ) A、 B、 C、 D、11. 如图,在中, , , , 则的内切圆半径r长为( )
A、 B、 C、 D、11. 如图,在中, , , , 则的内切圆半径r长为( )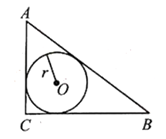 A、1.5 B、1 C、2 D、1.212. 如图(1),在平面直角坐标系中,矩形 在第一象限,且 轴,直线 沿 轴正方向平移,在平移过程中,直线被矩形 截得的线段长为 ,直线在 轴上平移的距离为 , 、 间的函数关系图象如图(2)所示,那么矩形 的面积为( )
A、1.5 B、1 C、2 D、1.212. 如图(1),在平面直角坐标系中,矩形 在第一象限,且 轴,直线 沿 轴正方向平移,在平移过程中,直线被矩形 截得的线段长为 ,直线在 轴上平移的距离为 , 、 间的函数关系图象如图(2)所示,那么矩形 的面积为( ) A、 B、 C、8 D、10
A、 B、 C、8 D、10二、填空题
-
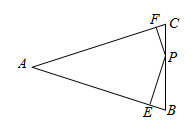
13. 分解因式: .14. 不等式组的解集为 .15. 一个不透明的口袋中有两个完全相同的小球,把它们分别标号为1,2.随机摸取一个小球后,放回并摇匀,再随机摸取一个小球,两次取出的小球标号的和等于4的概率为 .16. 如图, 中, 是 上任意一点, 于点 于点F,若 ,则 .
 17. 如图,在平面直角坐标系中, 的顶点坐标分别为: , , .已知 ,作点N关于点 的对称点 ,点 关于点 的对称点 ,点 关于点 的对称点 ,点 关于点 的对称点 ,点 关于点 的对称点 ,…,依此类推,则点 的坐标为.
17. 如图,在平面直角坐标系中, 的顶点坐标分别为: , , .已知 ,作点N关于点 的对称点 ,点 关于点 的对称点 ,点 关于点 的对称点 ,点 关于点 的对称点 ,点 关于点 的对称点 ,…,依此类推,则点 的坐标为.
三、解答题
-
18.(1)、计算: .(2)、化简: .19. 高尔基说:“书,是人类进步的阶梯”阅读可以启智增慧,拓展视野,…为了解学生寒假阅读情况,开学初学校进行了问卷调查,并对部分学生假期(24天)的阅读总时间作了随机抽样分析.设被抽样的每位同学寒假阅读的总时间为t(小时),阅读总时间分为四个类别:A(0≤t<12),B(12≤t<24),C(24≤t<36),D(t≥36),将分类结果制成两幅统计图(尚不完整).根据以上信息,回答下列问题:
 (1)、本次抽样的样本容量为;(2)、补全条形统计图;(3)、扇形统计图中a的值为 , 圆心角β的度数为;(4)、若该校有2000名学生,估计寒假阅读的总时间少于24小时的学生有多少名?20. 如图,矩形ABCD中,AB=8,AD=6,点O是对角线BD的中点,过点O的直线分别交AB、CD边于点E、F.
(1)、本次抽样的样本容量为;(2)、补全条形统计图;(3)、扇形统计图中a的值为 , 圆心角β的度数为;(4)、若该校有2000名学生,估计寒假阅读的总时间少于24小时的学生有多少名?20. 如图,矩形ABCD中,AB=8,AD=6,点O是对角线BD的中点,过点O的直线分别交AB、CD边于点E、F. (1)、求证:四边形DEBF是平行四边形;(2)、当DE=DF时,求EF的长.21. 某公司生产的一种营养品信息如下表.已知甲食材每千克的进价是乙食材的2倍,用80元购买的甲食材比用20元购买的乙食材多1千克.
(1)、求证:四边形DEBF是平行四边形;(2)、当DE=DF时,求EF的长.21. 某公司生产的一种营养品信息如下表.已知甲食材每千克的进价是乙食材的2倍,用80元购买的甲食材比用20元购买的乙食材多1千克.营养品信息表
营养成分
每千克含铁42毫克
配料表
原料
每千克含铁
甲食材
50毫克
乙食材
10毫克
规格
每包食材含量
每包单价
A包装
1千克
45元
B包装
0.25千克
12元
(1)、问甲、乙两种食材每千克进价分别是多少元?(2)、该公司每日用18000元购进甲、乙两种食材并恰好全部用完.①问每日购进甲、乙两种食材各多少千克?
②已知每日其他费用为2000元,且生产的营养品当日全部售出.若A的数量不低于B的数量,则A为多少包时,每日所获总利润最大?最大总利润为多少元?
22. 今年是建党100周年,学校新装了国旗旗杆(如图所示),星期一该校全体学生在国旗前举行了升旗仪式.仪式结束后,站在国旗正前方的小明在A处测得国旗D处的仰角为 ,站在同一队列B处的小刚测得国旗C处的仰角为 ,已知小明目高 米,距旗杆 的距离为15.8米,小刚目高 米,距小明24.2米,求国旗的宽度 是多少米?(最后结果保留一位小数)(参考数据: )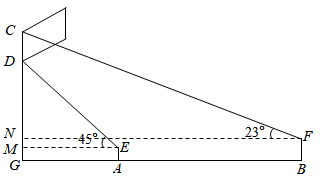 23. 已知点为函数()图象上任意一点,连接并延长至点 , 使 , 过点作轴交函数图象于点 , 连接 .
23. 已知点为函数()图象上任意一点,连接并延长至点 , 使 , 过点作轴交函数图象于点 , 连接 . (1)、如图1,若点的坐标为 , 求及点的坐标;(2)、如图2,过点作 , 垂足为 , 求四边形的面积.24. 如图,AB是 直径,弦 ,垂足为点E . 弦BF交CD于点G , 点P在CD延长线上,且 .
(1)、如图1,若点的坐标为 , 求及点的坐标;(2)、如图2,过点作 , 垂足为 , 求四边形的面积.24. 如图,AB是 直径,弦 ,垂足为点E . 弦BF交CD于点G , 点P在CD延长线上,且 .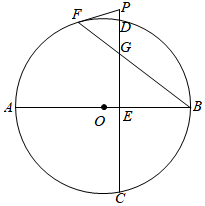 (1)、求证:PF为 切线;(2)、若 , , ,求PF的长.25. 如图,抛物线 经过 , 两点,与 轴交于点 ,连接 .
(1)、求证:PF为 切线;(2)、若 , , ,求PF的长.25. 如图,抛物线 经过 , 两点,与 轴交于点 ,连接 . (1)、求该抛物线的函数表达式;(2)、如图2,直线 : 经过点A,点 为直线 上的一个动点,且位于 轴的上方,点 为抛物线上的一个动点,当 轴时,作 ,交抛物线于点 (点 在点 的右侧),以 , 为邻边构造矩形 ,求该矩形周长的最小值;(3)、如图3,设抛物线的顶点为 ,在(2)的条件下,当矩形 的周长取最小值时,抛物线上是否存在点 ,使得 ?若存在,请求出点 的坐标;若不存在,请说明理由.
(1)、求该抛物线的函数表达式;(2)、如图2,直线 : 经过点A,点 为直线 上的一个动点,且位于 轴的上方,点 为抛物线上的一个动点,当 轴时,作 ,交抛物线于点 (点 在点 的右侧),以 , 为邻边构造矩形 ,求该矩形周长的最小值;(3)、如图3,设抛物线的顶点为 ,在(2)的条件下,当矩形 的周长取最小值时,抛物线上是否存在点 ,使得 ?若存在,请求出点 的坐标;若不存在,请说明理由.