山东省聊城市冠县2022年中考一模数学试题
试卷更新日期:2022-05-26 类型:中考模拟
一、单选题
-
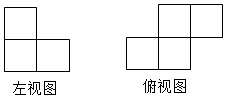
1. 下列整式中,是二次单项式的是( )A、x2+1 B、xy C、x2y D、22x2. 由若干个完全相同的小立方块搭成的几何体的左视图和俯视图如图所示,则搭成该几何体所用的小立方块的个数可能是( )
 A、4个 B、5个 C、7个 D、8个3. 如图, , , 平分 , 则的度数为( )
A、4个 B、5个 C、7个 D、8个3. 如图, , , 平分 , 则的度数为( )
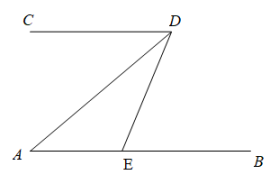 A、 B、 C、 D、4. 设 , 则( )A、 B、 C、 D、5. 某校举行学生会成员的竞选活动,对竞选者从民主测评和演讲两个方面进行考核,两项成绩均按百分制计,规定民主测评的成绩占40%,演讲的成绩占60%,小新同学的民主测评和演讲的成绩分别为80分和90分,则他的最终成绩是( )A、83分 B、84分 C、85分 D、86分6. 已知实数 在数轴上的对应点位置如图所示,则化简 的结果是( )
A、 B、 C、 D、4. 设 , 则( )A、 B、 C、 D、5. 某校举行学生会成员的竞选活动,对竞选者从民主测评和演讲两个方面进行考核,两项成绩均按百分制计,规定民主测评的成绩占40%,演讲的成绩占60%,小新同学的民主测评和演讲的成绩分别为80分和90分,则他的最终成绩是( )A、83分 B、84分 C、85分 D、86分6. 已知实数 在数轴上的对应点位置如图所示,则化简 的结果是( )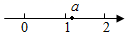 A、 B、 C、1 D、7. 如图, 的顶点是正方形网格的格点,则 的值为( )
A、 B、 C、1 D、7. 如图, 的顶点是正方形网格的格点,则 的值为( )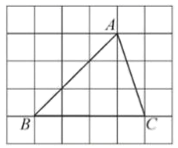 A、 B、 C、 D、8. 关于x的一元二次方程x2﹣2x+m﹣1=0有两个不相等的实数根,则实数m的取值范围是( )A、m≥2 B、m≤2 C、m>2 D、m<29. 如图,面积为18的正方形 内接于⊙O,则 的长度为( )
A、 B、 C、 D、8. 关于x的一元二次方程x2﹣2x+m﹣1=0有两个不相等的实数根,则实数m的取值范围是( )A、m≥2 B、m≤2 C、m>2 D、m<29. 如图,面积为18的正方形 内接于⊙O,则 的长度为( )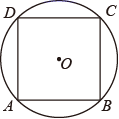 A、 B、 C、 D、10. 如图,菱形ABCD中, ,点P从点B出发,沿折线 方向移动,移动到点D停止.在 形状的变化过程中,依次出现的特殊三角形是( )
A、 B、 C、 D、10. 如图,菱形ABCD中, ,点P从点B出发,沿折线 方向移动,移动到点D停止.在 形状的变化过程中,依次出现的特殊三角形是( )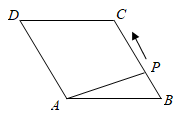 A、直角三角形→等边三角形→等腰三角形→直角三角形 B、直角三角形→等腰三角形→直角三角形→等边三角形 C、直角三角形→等边三角形→直角三角形→等腰三角形 D、等腰三角形→等边三角形→直角三角形→等腰三角形11. 图1是第七届国际数学教育大会(ICME)的会徽,在其主体图案中选择两个相邻的直角三角形,恰好能组合得到如图2所示的四边形 .若 . ,则 的值为( )
A、直角三角形→等边三角形→等腰三角形→直角三角形 B、直角三角形→等腰三角形→直角三角形→等边三角形 C、直角三角形→等边三角形→直角三角形→等腰三角形 D、等腰三角形→等边三角形→直角三角形→等腰三角形11. 图1是第七届国际数学教育大会(ICME)的会徽,在其主体图案中选择两个相邻的直角三角形,恰好能组合得到如图2所示的四边形 .若 . ,则 的值为( ) A、 B、 C、 D、12. 如图1,小球从左侧的斜坡滚下,到达底端后又沿着右侧斜坡向上滚,在这个过程中,小球的运动速度v(单位:m/s)与运动时间t (单位:s)的函数图象如图2,则该小球的运动路程y(单位:m)与运动时间t(单位:s)之间的函数图象大致是( )
A、 B、 C、 D、12. 如图1,小球从左侧的斜坡滚下,到达底端后又沿着右侧斜坡向上滚,在这个过程中,小球的运动速度v(单位:m/s)与运动时间t (单位:s)的函数图象如图2,则该小球的运动路程y(单位:m)与运动时间t(单位:s)之间的函数图象大致是( ) A、
A、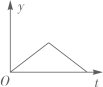 B、
B、 C、
C、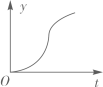 D、
D、
二、填空题
-
13. 因式分解: .14. 计算: 的结果是.15. 从﹣2,4,5这3个数中,任取两个数作为点P的坐标,则点P在第四象限的概率是.16. 如图,在平面直角坐标系 中,点A在 轴负半轴上,点B在 轴正半轴上,⊙D经过A , B , O , C四点,∠ACO=120°,AB=4,则圆心点D的坐标是
 17. 如图,在正方形ABCD中,点M、N分别为边CD、BC上的点,且DM=CN,AM与DN交于点P,连接AN,点Q为AN的中点,连接PQ,BQ,若AB=8,DM=2,给出以下结论:①AM⊥DN;②∠MAN=∠BAN;③PQN≌BQN;④PQ=5.其中正确的结论有 (填上所有正确结论的序号)
17. 如图,在正方形ABCD中,点M、N分别为边CD、BC上的点,且DM=CN,AM与DN交于点P,连接AN,点Q为AN的中点,连接PQ,BQ,若AB=8,DM=2,给出以下结论:①AM⊥DN;②∠MAN=∠BAN;③PQN≌BQN;④PQ=5.其中正确的结论有 (填上所有正确结论的序号)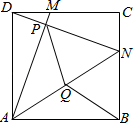
三、解答题
-
18. 解不等式组, , 在数轴上表示解集并写出它的所有非正整数解.19. 在中国共产党成立一百周年之际,某校举行了以“童心向党”为主题的知识竞赛活动.发现该校全体学生的竞赛成绩(百分制)均不低于60分,现从中随机抽取名学生的竞赛成绩进行整理和分析(成绩得分用表示,共分成四组),并绘制成如下的竞赛成绩分组统计表和扇形统计图.其中“”这组的数据如下:
90,92,93,95,95,96,96,96,97,100.
竞赛成绩分组统计表
组别
竞赛成绩分组
频数
平均分
1
8
65
2
75
3
88
4
10
95
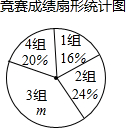
请根据以上信息,解答下列问题:
(1)、;(2)、“”这组数据的众数是分;(3)、随机抽取的这名学生竞赛成绩的平均分是分;(4)、若学生竞赛成绩达到96分以上(含96分)获奖,请你估计全校1200名学生中获奖的人数.20. 某药店新进一批桶装消毒液,每桶进价35元,原计划以每桶55元的价格销售,为更好地助力疫情防控,现决定降价销售.已知这种消毒液销售量(桶)与每桶降价(元)()之间满足一次函数关系,其图象如图所示: (1)、求与之间的函数关系式;(2)、在这次助力疫情防控活动中,该药店仅获利1760元.这种消毒液每桶实际售价多少元?21. 如图,四边形ABCD是菱形,对角线AC,BD相交于点O,△BOC≌△CEB.
(1)、求与之间的函数关系式;(2)、在这次助力疫情防控活动中,该药店仅获利1760元.这种消毒液每桶实际售价多少元?21. 如图,四边形ABCD是菱形,对角线AC,BD相交于点O,△BOC≌△CEB.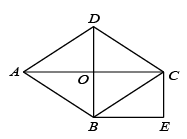 (1)、求证:四边形OBEC是矩形;(2)、若∠ABC=120°,AB=6,求矩形OBEC的周长.22. 学校运动场的四角各有一盏探照灯,其中一盏探照灯B的位置如图所示,已知坡长AC=12m,坡角α为30°,灯光受灯罩的影响,最远端的光线与地面的夹角β为27°,最近端的光线恰好与地面交于坡面的底端C处,且与地面的夹角为60°,A、B、C、D在同一平面上.(结果精确到0.1m.参考数据:sin27°≈0.45,cos27°≈0.89,tan27°≈0.50, 1.73.)
(1)、求证:四边形OBEC是矩形;(2)、若∠ABC=120°,AB=6,求矩形OBEC的周长.22. 学校运动场的四角各有一盏探照灯,其中一盏探照灯B的位置如图所示,已知坡长AC=12m,坡角α为30°,灯光受灯罩的影响,最远端的光线与地面的夹角β为27°,最近端的光线恰好与地面交于坡面的底端C处,且与地面的夹角为60°,A、B、C、D在同一平面上.(结果精确到0.1m.参考数据:sin27°≈0.45,cos27°≈0.89,tan27°≈0.50, 1.73.) (1)、求灯杆AB的高度;(2)、求CD的长度.23. 如图,点在反比例函数的图象上,轴,且交y轴于点C,交反比例函数于点B,已知 .
(1)、求灯杆AB的高度;(2)、求CD的长度.23. 如图,点在反比例函数的图象上,轴,且交y轴于点C,交反比例函数于点B,已知 .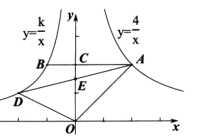 (1)、求直线的解析式;(2)、求反比例函数的解析式;(3)、点D为反比例函数上一动点,连接交y轴于点E,当E为中点时,求的面积.24. 如图,AB为⊙O的直径,直线l与⊙O相切于点C,AD⊥l,垂足为D,AD交⊙O于点E,连接CE.
(1)、求直线的解析式;(2)、求反比例函数的解析式;(3)、点D为反比例函数上一动点,连接交y轴于点E,当E为中点时,求的面积.24. 如图,AB为⊙O的直径,直线l与⊙O相切于点C,AD⊥l,垂足为D,AD交⊙O于点E,连接CE.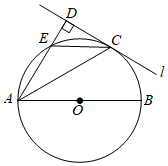 (1)、求证:∠CAD=∠CAB;(2)、若EC=4,sin∠CAD , 求⊙O的半径.25. 科研人员为了研究弹射器的某项性能,利用无人机测量小钢球竖直向上运动的相关数据.无人机上升到离地面30米处开始保持匀速竖直上升,此时,在地面用弹射器(高度不计)竖直向上弹射一个小钢球(忽路空气阻力),在1秒时,它们距离地面都是35米,在6秒时,它们距离地面的高度也相同.其中无人机离地面高度(米)与小钢球运动时间(秒)之间的函数关系如图所示;小钢球离地面高度(米)与它的运动时间(秒)之间的函数关系如图中抛物线所示.
(1)、求证:∠CAD=∠CAB;(2)、若EC=4,sin∠CAD , 求⊙O的半径.25. 科研人员为了研究弹射器的某项性能,利用无人机测量小钢球竖直向上运动的相关数据.无人机上升到离地面30米处开始保持匀速竖直上升,此时,在地面用弹射器(高度不计)竖直向上弹射一个小钢球(忽路空气阻力),在1秒时,它们距离地面都是35米,在6秒时,它们距离地面的高度也相同.其中无人机离地面高度(米)与小钢球运动时间(秒)之间的函数关系如图所示;小钢球离地面高度(米)与它的运动时间(秒)之间的函数关系如图中抛物线所示.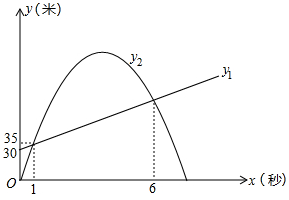 (1)、直接写出与之间的函数关系式;(2)、求出与之间的函数关系式;(3)、小钢球弹射1秒后直至落地时,小钢球和无人机的高度差最大是多少米?
(1)、直接写出与之间的函数关系式;(2)、求出与之间的函数关系式;(3)、小钢球弹射1秒后直至落地时,小钢球和无人机的高度差最大是多少米?