山东省济宁邹城市2022年中考一模数学试题
试卷更新日期:2022-05-26 类型:中考模拟
一、单选题
-
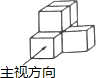
1. 下列图形中,既是轴对称图形又是中心对称图形的是( )A、等边三角形 B、平行四边形 C、正五边形 D、圆2. 下列等式成立的是( )A、 B、 C、 D、3. 蜜蜂建造的蜂巢既坚固又省料,其厚度约为0.000073米,将0.000073用科学记数法表示为( )A、 B、 C、 D、4. 如图是由六个相同的小正方体组成的立方体图形,它的俯视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 5. 不等式组的解在数轴上表示正确的是( )A、
5. 不等式组的解在数轴上表示正确的是( )A、 B、
B、 C、
C、 D、
D、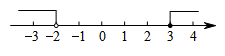 6. 如图所示,将含有30°角的三角板的直角顶点放在相互平行的两条直线其中一条上,若∠1=42°32′,则∠2的度数( )
6. 如图所示,将含有30°角的三角板的直角顶点放在相互平行的两条直线其中一条上,若∠1=42°32′,则∠2的度数( ) A、17°28′ B、18°28′ C、27°28′ D、27°32′7. 某种商品的进价为160元,出售时的标价为240元,后来由于该商品积压,商店准备打折出售,但要保持利润率不低于5%,则至多可打( )A、6折 B、7折 C、8折 D、9折8. 一平行四边形的一条边长为6,两条对角线的长分别为8和 , 这个平行四边形是( )A、正方形 B、矩形 C、菱形 D、非特殊平行四边形9. 某赛季甲、乙两名篮球运动员12场比赛得分情况用图表示如下:
A、17°28′ B、18°28′ C、27°28′ D、27°32′7. 某种商品的进价为160元,出售时的标价为240元,后来由于该商品积压,商店准备打折出售,但要保持利润率不低于5%,则至多可打( )A、6折 B、7折 C、8折 D、9折8. 一平行四边形的一条边长为6,两条对角线的长分别为8和 , 这个平行四边形是( )A、正方形 B、矩形 C、菱形 D、非特殊平行四边形9. 某赛季甲、乙两名篮球运动员12场比赛得分情况用图表示如下:
对这两名运动员的成绩进行比较,下列四个结论中,错误的是( )
A、甲运动员得分的极差大于乙运动员得分的极差 B、甲运动员得分的的中位数大于乙运动员得分的的中位数 C、甲运动员的得分平均数大于乙运动员的得分平均数 D、甲运动员的成绩比乙运动员的成绩稳定10. 如图所示:边长分别为 和 的两个正方形,其一边在同一水平线上,小正方形沿该水平线自左向右匀速穿过大正方形,设穿过的时间为 ,大正方形内除去小正方形部分的面积为 (阴影部分),那么 与 的大致图象应为( ). A、
A、 B、
B、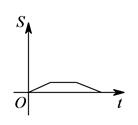 C、
C、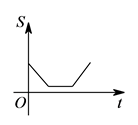 D、
D、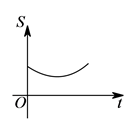
二、填空题
-
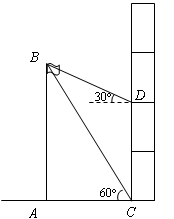
11. 函数 的自变量 的取值范围是12. 若点和点关于y轴对称,则点在第象限.13. 某校研究性学习小组测量学校旗杆AB的高度,如图在教学楼一楼C处测得旗杆顶部的仰角为60°,在教学楼三楼D处测得旗杆顶部的仰角为30°,旗杆底部与教学楼一楼在同一水平线上,已知每层楼的高度为3米,则旗杆AB的高度为米.
 14. 小明从家步行到学校需走的路程为1800米.图中的折线OAB反映了小明从家步行到学校所走的路程s(米)与时间t(分钟)的函数关系,根据图象提供的信息,当小明从家出发去学校步行15分钟时,到学校还需步行米.
14. 小明从家步行到学校需走的路程为1800米.图中的折线OAB反映了小明从家步行到学校所走的路程s(米)与时间t(分钟)的函数关系,根据图象提供的信息,当小明从家出发去学校步行15分钟时,到学校还需步行米.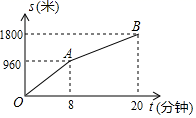 15. 如图,矩形ABCD中,BD为对角线,将矩形ABCD沿BE、BF所在直线折叠,使点A落在BD上的点M处,点C落在BD上的点N处,连结EF.已知 , , 则EF的长为 .
15. 如图,矩形ABCD中,BD为对角线,将矩形ABCD沿BE、BF所在直线折叠,使点A落在BD上的点M处,点C落在BD上的点N处,连结EF.已知 , , 则EF的长为 .
三、解答题
-
16. 先化简,再求值: •÷ , 其中a满足a2-a=0.17. “校园手机”现象越来越受到社会的关注.小丽在“统计实习”活动中随机调查了学校若干名学生家长对“中学生带手机到学校”现象的看法,统计整理并制作了如下的统计图:
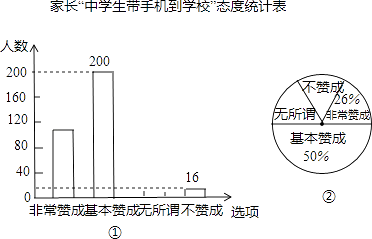 (1)、求这次调查的家长总数及家长表示“无所谓”的人数,并补全图①;(2)、求图②中表示家长“无所谓”的圆心角的度数;(3)、从这次接受调查的家长中,随机抽查一个,恰好是“不赞成”态度的家长的概率是多少.18. 如图,四边形内接于 , 且为直径, , 过A点的的垂线交的延长线于点E.
(1)、求这次调查的家长总数及家长表示“无所谓”的人数,并补全图①;(2)、求图②中表示家长“无所谓”的圆心角的度数;(3)、从这次接受调查的家长中,随机抽查一个,恰好是“不赞成”态度的家长的概率是多少.18. 如图,四边形内接于 , 且为直径, , 过A点的的垂线交的延长线于点E. (1)、求证:;(2)、如果 , 求图中阴影的面积.19. 如图,在平面直角坐标系中直线y=x﹣2与y轴相交于点A,与反比例函数在第一象限内的图象相交于点B(m,2).
(1)、求证:;(2)、如果 , 求图中阴影的面积.19. 如图,在平面直角坐标系中直线y=x﹣2与y轴相交于点A,与反比例函数在第一象限内的图象相交于点B(m,2).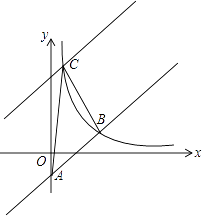 (1)、求反比例函数的关系式;(2)、将直线y=x﹣2向上平移后与反比例函数图象在第一象限内交于点C,且△ABC的面积为18,求平移后的直线的函数关系式.20. 如图,是的高,是的中线, , , , 直线交于点M,交于点N.
(1)、求反比例函数的关系式;(2)、将直线y=x﹣2向上平移后与反比例函数图象在第一象限内交于点C,且△ABC的面积为18,求平移后的直线的函数关系式.20. 如图,是的高,是的中线, , , , 直线交于点M,交于点N. (1)、求证:四边形是平行四边形;(2)、求的度数;(3)、当 , 时,求线段的长.21. 利达经销店为某工厂代销一种建筑材料(这里的代销是指厂家先免费提供货源,待货物售出后再进行结算,未售出的由厂家负责处理).当每吨售价为260元时,月销售量为45吨.该经销店为提高经营利润,准备采取降价的方式进行促销.经市场调查发现:当每吨售价每下降10元时,月销售量就会增加7.5吨.综合考虑各种因素,每售出一吨建筑材料共需支付厂家及其它费用100元.设每吨材料售价为x(元),该经销店的月利润为y(元).(1)、当每吨售价是240元时,计算此时的月销售量;(2)、求出y与x的函数关系式(不要求写出x的取值范围);(3)、该经销店要获得最大月利润,售价应定为每吨多少元?22. 如图,已知二次函数的图象交x轴分别于A,D两点,交y轴于B点,顶点为C.
(1)、求证:四边形是平行四边形;(2)、求的度数;(3)、当 , 时,求线段的长.21. 利达经销店为某工厂代销一种建筑材料(这里的代销是指厂家先免费提供货源,待货物售出后再进行结算,未售出的由厂家负责处理).当每吨售价为260元时,月销售量为45吨.该经销店为提高经营利润,准备采取降价的方式进行促销.经市场调查发现:当每吨售价每下降10元时,月销售量就会增加7.5吨.综合考虑各种因素,每售出一吨建筑材料共需支付厂家及其它费用100元.设每吨材料售价为x(元),该经销店的月利润为y(元).(1)、当每吨售价是240元时,计算此时的月销售量;(2)、求出y与x的函数关系式(不要求写出x的取值范围);(3)、该经销店要获得最大月利润,售价应定为每吨多少元?22. 如图,已知二次函数的图象交x轴分别于A,D两点,交y轴于B点,顶点为C. (1)、求抛物线的对称轴;(2)、求;(3)、在y轴上是否存在一点P,使得以P,B,D三点为顶点的三角形与相似?如果存在,请求出点P的坐标:如果不存在,请说明理由.
(1)、求抛物线的对称轴;(2)、求;(3)、在y轴上是否存在一点P,使得以P,B,D三点为顶点的三角形与相似?如果存在,请求出点P的坐标:如果不存在,请说明理由.