山东省济南市历下区2022年九年级数学二模试题
试卷更新日期:2022-05-26 类型:中考模拟
一、单选题
-
1. ﹣3的相反数是( )A、﹣3 B、﹣ C、3 D、±32. 根据国家统计局数据显示,我国冰雪运动参与人数达到346000000人.数据346000000用科学记数法表示为( )A、 B、 C、 D、3. 如图,从左面看如图所示的几何体得到的平面图形是( )
 A、
A、 B、
B、 C、
C、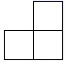 D、
D、 4. 如图,直线、与直线相交,且 , 若 , 则的度数( )
4. 如图,直线、与直线相交,且 , 若 , 则的度数( ) A、 B、 C、 D、5. 手机已逐渐成为人们日常通讯的主要工具,其背后离不开通讯运营商的市场支持,下图展现的是我国四大通讯运营商的企业图标,其中是轴对称图形的是( )A、
A、 B、 C、 D、5. 手机已逐渐成为人们日常通讯的主要工具,其背后离不开通讯运营商的市场支持,下图展现的是我国四大通讯运营商的企业图标,其中是轴对称图形的是( )A、 B、
B、 C、
C、 D、
D、 6. 下列运算正确的是( )A、 B、 C、 D、7. 如图,把△ABC先向右平移3个单位,再向上平移2个单位得到△DEF,则顶点C(0,-1)对应点的坐标为( )
6. 下列运算正确的是( )A、 B、 C、 D、7. 如图,把△ABC先向右平移3个单位,再向上平移2个单位得到△DEF,则顶点C(0,-1)对应点的坐标为( )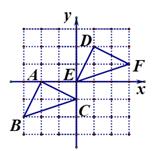 A、(0,0) B、(1,2) C、(1,3) D、(3,1)8. 不透明袋子中装有红、绿小球各一个,除颜色外无其它差别,随机摸出一个小球后,放回并摇匀,再随机摸出一个,两次都摸到颜色相同的球的概率为( )A、 B、 C、 D、9. 在同一平面直角坐标系中,函数y=mx+m(m≠0)与
A、(0,0) B、(1,2) C、(1,3) D、(3,1)8. 不透明袋子中装有红、绿小球各一个,除颜色外无其它差别,随机摸出一个小球后,放回并摇匀,再随机摸出一个,两次都摸到颜色相同的球的概率为( )A、 B、 C、 D、9. 在同一平面直角坐标系中,函数y=mx+m(m≠0)与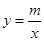 (m≠0)的图象可能是( ) A、
(m≠0)的图象可能是( ) A、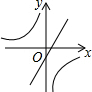 B、
B、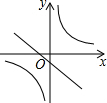 C、
C、 D、
D、 10. 如图,热气球的探测器显示,从热气球A处看一栋楼顶部B处的仰角为30°,看这栋楼底部C处的俯角为60°,热气球A处与楼的水平距离为30m,则这栋楼的高度为( )
10. 如图,热气球的探测器显示,从热气球A处看一栋楼顶部B处的仰角为30°,看这栋楼底部C处的俯角为60°,热气球A处与楼的水平距离为30m,则这栋楼的高度为( ) A、 B、 C、75m D、11. 如图,在已知的中,按以下步骤作图:①分别以B,C为圆心,以大于的长为半径作弧,两弧相交于两点M,N;②作直线MN交AB于点D,连接CD.若 , , 则∠ACB的度数为( )
A、 B、 C、75m D、11. 如图,在已知的中,按以下步骤作图:①分别以B,C为圆心,以大于的长为半径作弧,两弧相交于两点M,N;②作直线MN交AB于点D,连接CD.若 , , 则∠ACB的度数为( )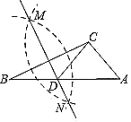 A、105° B、100° C、95° D、90°12. 已知二次函数y=ax2+2ax+3a-2(a是常数,且a≠0)的图象过点M(x1 , -1),N(x2 , -1),若MN的长不小于2,则a的取值范围是( )A、a≥ B、0<a≤ C、- ≤a<0 D、a≤-
A、105° B、100° C、95° D、90°12. 已知二次函数y=ax2+2ax+3a-2(a是常数,且a≠0)的图象过点M(x1 , -1),N(x2 , -1),若MN的长不小于2,则a的取值范围是( )A、a≥ B、0<a≤ C、- ≤a<0 D、a≤-二、填空题
-
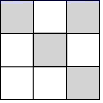
13. 因式分解: .14. 一个小球在如图所示的地板上自由滚动,并随机停在某块方砖上 . 如果每一块方砖除颜色外完全相同,那么小球最终停留在黑砖上的概率是 .
 15. 若分式与值相等,则x的值为 .16. 小明发现交通指示牌中“停车让行标志”可以看成是正八边形,如图所示,则°.
15. 若分式与值相等,则x的值为 .16. 小明发现交通指示牌中“停车让行标志”可以看成是正八边形,如图所示,则°. 17. 某快递公司每天上午9:00-10:00为集中揽件和派件时段,甲仓库用来揽收快件,乙仓库用来派发快件,该时段内甲、乙两仓库的快件数量y(件)与时间x(分)之间的函数图象如图所示,那么当两仓库快递件数相同时,此刻的时间为;
17. 某快递公司每天上午9:00-10:00为集中揽件和派件时段,甲仓库用来揽收快件,乙仓库用来派发快件,该时段内甲、乙两仓库的快件数量y(件)与时间x(分)之间的函数图象如图所示,那么当两仓库快递件数相同时,此刻的时间为; 18. 矩形ABCD中AB=10,BC=8,E为AD边上一点,沿CE将△CDE对折,使点D正好落在AB边上,则tan∠AFE= .
18. 矩形ABCD中AB=10,BC=8,E为AD边上一点,沿CE将△CDE对折,使点D正好落在AB边上,则tan∠AFE= .
三、解答题
-
19. 计算: .20. 求下列不等式组的整数解.21. 如图,在菱形ABCD中,CE=CF.求证:AE=AF.
 22. “双减”政策落实下,学生在完成作业之余,每天有更多时间进行体育锻炼.为了了解学生体育锻炼时间具体情况,某中学入学后,对八,九年级学生每天体育锻炼时间进行了问卷调查,现从八、九年级各抽取了15名同学的调查数据进行整理、描述和分析如下:(调查数据用x表示,共分成四组:A: , B: , C: , D: , 单位为小时)
22. “双减”政策落实下,学生在完成作业之余,每天有更多时间进行体育锻炼.为了了解学生体育锻炼时间具体情况,某中学入学后,对八,九年级学生每天体育锻炼时间进行了问卷调查,现从八、九年级各抽取了15名同学的调查数据进行整理、描述和分析如下:(调查数据用x表示,共分成四组:A: , B: , C: , D: , 单位为小时)八年级抽取的15名同学的调查数据是:
0.1,0.4,0.6,0.7,0.8,1,1.2,1.2,1.2,1.3,1.3,1.4,1.6,1.8,2
九年级抽取的15名同学调查数据中:
A,C两组同学的调查数据是:0.4,1.2,1.3,1.4,1.4,1.4,1.4,B、D两组数据个数相等,
年级
八年级
九年级
平均数
1.1
1.3
中位数
1.2
a
众数
b
1.4

根据以上信息,解答下列问题:
(1)、九年级B组数据的个数是;(2)、直接写出上述图表中a,b,m的值: , , ;(3)、若每天体育锻炼超过1个小时视为有良好的生活习惯,请根据调查结果,估计该校八年级600人中有良好生活习惯的学生人数是多少人.23. 如图,BE是⊙O的直径,点A和点D是⊙O上的两点,过点A作⊙O的切线交BE延长线于点C. (1)、若 , 求∠C的度数;(2)、若 , , 求⊙O半径的长.24. 在疫情期间,学校购买甲、乙两种消毒液,已知购买3桶甲种消毒液和4桶乙种消毒液共需170元,购买2桶乙种消毒液比购买3桶甲种消毒液少用50元.(1)、求购买甲、乙两种消毒液每桶各需多少元?(2)、若要购买甲、乙两种消毒液共21桶,且总费用不超过540元,求至多可购进甲种消毒液多少桶?25. 如图,直线y=ax+1与x轴、y轴分别相交于A , B两点,与双曲线y= (x>0)相交于点P , PC⊥x轴于点C , 且PC=2,tan∠BAO= .
(1)、若 , 求∠C的度数;(2)、若 , , 求⊙O半径的长.24. 在疫情期间,学校购买甲、乙两种消毒液,已知购买3桶甲种消毒液和4桶乙种消毒液共需170元,购买2桶乙种消毒液比购买3桶甲种消毒液少用50元.(1)、求购买甲、乙两种消毒液每桶各需多少元?(2)、若要购买甲、乙两种消毒液共21桶,且总费用不超过540元,求至多可购进甲种消毒液多少桶?25. 如图,直线y=ax+1与x轴、y轴分别相交于A , B两点,与双曲线y= (x>0)相交于点P , PC⊥x轴于点C , 且PC=2,tan∠BAO= . (1)、求一次函数系数a的值;(2)、求双曲线的解析式;(3)、若点Q为双曲线上点P右侧一点,且QH⊥x轴于H , 当以点Q , C , H为顶点的三角形与△AOB相似时,求点Q的坐标.
(1)、求一次函数系数a的值;(2)、求双曲线的解析式;(3)、若点Q为双曲线上点P右侧一点,且QH⊥x轴于H , 当以点Q , C , H为顶点的三角形与△AOB相似时,求点Q的坐标.

