山东省济南市历城区2022年中考数学一模试卷
试卷更新日期:2022-05-26 类型:中考模拟
一、单选题
-
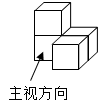
1. ﹣3的绝对值是( )A、﹣3 B、3 C、- D、2. 如图是由四个相同的小正方体组成的立体图形,它的俯视图为( )
 A、
A、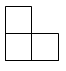 B、
B、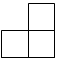 C、
C、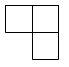 D、
D、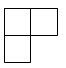 3. 目前全球新型冠状病毒肺炎疫情防控形势依旧严峻,我们应该坚持“勤洗手,戴口罩,常通风”.一双没有洗过的手,带有各种细菌约万个,将数据用科学记数法表示是( )A、 B、 C、 D、4. 如图所示,已知 , , , 的度数是( )
3. 目前全球新型冠状病毒肺炎疫情防控形势依旧严峻,我们应该坚持“勤洗手,戴口罩,常通风”.一双没有洗过的手,带有各种细菌约万个,将数据用科学记数法表示是( )A、 B、 C、 D、4. 如图所示,已知 , , , 的度数是( )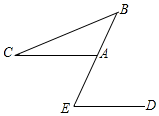 A、 B、 C、 D、5. 实数 在数轴上的对应点的位置如图所示,下列关系式不成立的是( )
A、 B、 C、 D、5. 实数 在数轴上的对应点的位置如图所示,下列关系式不成立的是( ) A、 B、 C、 D、6. 下列四个图形中,既是轴对称图形又是中心对称图形的是( )A、
A、 B、 C、 D、6. 下列四个图形中,既是轴对称图形又是中心对称图形的是( )A、 B、
B、 C、
C、 D、
D、 7. 下列运算正确的是( )A、 B、 C、 D、8. 一个不透明的布袋中,装有红、黄、白三种只有颜色不同的小球,其中红色小球有个,黄、白色小球的数目相同、为估计袋中黄色小球的数目,每次将袋中小球搅匀后摸出一个小球记下颜色,再次搅匀…多次试验发现摸到红球的频率是 , 则估计黄色小球的数目是( )A、2个 B、20个 C、40个 D、48个9. 如图,在平面直角坐标系中,四边形OABC是边长为1的正方形,顶点A、C分别在x轴的负半轴、y轴的正半轴上.若直线y=kx+2与边AB有公共点,则k的值可能为( )
7. 下列运算正确的是( )A、 B、 C、 D、8. 一个不透明的布袋中,装有红、黄、白三种只有颜色不同的小球,其中红色小球有个,黄、白色小球的数目相同、为估计袋中黄色小球的数目,每次将袋中小球搅匀后摸出一个小球记下颜色,再次搅匀…多次试验发现摸到红球的频率是 , 则估计黄色小球的数目是( )A、2个 B、20个 C、40个 D、48个9. 如图,在平面直角坐标系中,四边形OABC是边长为1的正方形,顶点A、C分别在x轴的负半轴、y轴的正半轴上.若直线y=kx+2与边AB有公共点,则k的值可能为( ) A、 B、 C、 D、310. 如图,在△ABC中,AB=AC,以点C为圆心,CB长为半径画弧,交AB于点B和点D,再分别以点B,D为圆心,大于BD长为半径画弧,两弧相交于点M,作射线CM交AB于点 E.若AD=3,BD=2,则EC的长度是( )
A、 B、 C、 D、310. 如图,在△ABC中,AB=AC,以点C为圆心,CB长为半径画弧,交AB于点B和点D,再分别以点B,D为圆心,大于BD长为半径画弧,两弧相交于点M,作射线CM交AB于点 E.若AD=3,BD=2,则EC的长度是( ) A、 B、 C、3 D、211. 3月中旬某中学校园内的樱花树正值盛花期,供全校师生驻足观赏. 如图,有一棵樱花树AB垂直于水平平台BC,通往平台有一斜坡CD,D,E在同一水平地面上,A,B,C,D,E均在同一平面内,已知BC=3米,CD=5米,DE=1米,斜坡CD的坡度是 ,李同学在水平地面E处测得树冠顶端A的仰角为62°,则樱花树的高度AB约为( )(参考数据:sin62°≈0.88,cos62°≈0.47,tan62°≈1.88)
A、 B、 C、3 D、211. 3月中旬某中学校园内的樱花树正值盛花期,供全校师生驻足观赏. 如图,有一棵樱花树AB垂直于水平平台BC,通往平台有一斜坡CD,D,E在同一水平地面上,A,B,C,D,E均在同一平面内,已知BC=3米,CD=5米,DE=1米,斜坡CD的坡度是 ,李同学在水平地面E处测得树冠顶端A的仰角为62°,则樱花树的高度AB约为( )(参考数据:sin62°≈0.88,cos62°≈0.47,tan62°≈1.88) A、 9.16米 B、12.04米 C、13.16米 D、15.04米12. 抛物线C1:y1=mx2-4mx+2n-1与平行于x轴的直线交于A、B两点,且A点坐标为(-1,2),请结合图象分析以下结论:①对称轴为直线x=2;②抛物线与y轴交点坐标为(0,-1);③m> ;④若抛物线C2:y2=ax2(a≠0)与线段AB恰有一个公共点,则a的取值范围是 ≤a<2;⑤不等式mx2-4mx+2n>0的解作为函数C1的自变量的取值时,对应的函数值均为正数,其中正确结论的个数有( )
A、 9.16米 B、12.04米 C、13.16米 D、15.04米12. 抛物线C1:y1=mx2-4mx+2n-1与平行于x轴的直线交于A、B两点,且A点坐标为(-1,2),请结合图象分析以下结论:①对称轴为直线x=2;②抛物线与y轴交点坐标为(0,-1);③m> ;④若抛物线C2:y2=ax2(a≠0)与线段AB恰有一个公共点,则a的取值范围是 ≤a<2;⑤不等式mx2-4mx+2n>0的解作为函数C1的自变量的取值时,对应的函数值均为正数,其中正确结论的个数有( ) A、2个 B、3个 C、4个 D、5个
A、2个 B、3个 C、4个 D、5个二、填空题
-
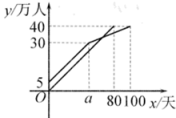
13. 分解因式a2﹣9a的结果是14. 某校欲从初三级部3名女生,2名男生中任选两名学生代表学校参加全市举办的“中国梦•青春梦”演讲比赛,则恰好选中一男一女的概率是 .15. 一个多边形的内角和与外角和之和为900°,则这个多边形的边数为.16. 若 ,则 的值为.17. 疫苗接种,利国利民.甲、乙两地分别对本地各40万人接种新冠疫苗.甲地在前期完成5万人接种后,甲、乙两地同时以相同速度接种,甲地经过a天后接种人数达到30万人,由于情况变化,接种速度放缓,结果100天完成接种任务.乙地80天完成接种任务.在某段时间内,甲、乙两地的接种人数y(万人)与各自接种时间x(天)之间的关系如图所示,当乙地完成接种任务时,甲地未接种疫苗的人数为万人.
 18. 如图,矩形纸片ABCD中,AB=2 , BC=10,将矩形纸片ABCD折叠,使C与点A重合,则折痕EF的长为 .
18. 如图,矩形纸片ABCD中,AB=2 , BC=10,将矩形纸片ABCD折叠,使C与点A重合,则折痕EF的长为 .
三、解答题
-
19. 计算: .20. 解下面一元一次不等式组,并写出它的所有非负整数解.
.
21. 如图,在▱ABCD中,对角线AC、BD相交于点O,过点O的直线分别交DA、BC延长线于点E、F.求证:AE=CF.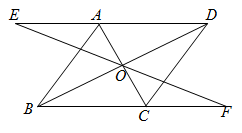 22. 为倡导绿色健康节约的生活方式,某社区开展“垃圾分类,从我做起”的活动,志愿者随机抽取了社区内50名居民,对其3月份垃圾分类投放次数进行了调查,并对数据进行了统计整理,以下是部分数据和不完整的统计图表:
22. 为倡导绿色健康节约的生活方式,某社区开展“垃圾分类,从我做起”的活动,志愿者随机抽取了社区内50名居民,对其3月份垃圾分类投放次数进行了调查,并对数据进行了统计整理,以下是部分数据和不完整的统计图表:信息1:垃圾分类投放次数分布表信息
组别
投放次数
频数
A
a
B
10
C
c
D
14
E
e
合计
50

信息3:C组包含的数据:12,12,10,12,13,10,11,13,12,11,13.
请结合以上信息完成下列问题:
(1)、统计表中的a= , e=;(2)、统计图中B组对应扇形的圆心角为度;(3)、C组数据的众数是 , 抽取的50名居民3月份垃圾分类投放次数的中位数是;(4)、根据调查结果,请你估计该社区2000名居民中3月份垃圾分类投放次数不少于15次的人数.23. 如图,AB是⊙O的直径,C为⊙O上一点,过点O作OD⊥AB,交AC的延长线于点D,交过点C的切线于点 E.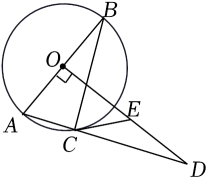 (1)、求证:∠DCE=∠ABC;(2)、若OA=3,AC=2,求线段CD的长.24. 某商场的运动服装专柜,对两种品牌的运动服分两次采购试销后,效益可观,计划继续采购进行销售.已知这两种服装过去两次的进货情况如下表.
(1)、求证:∠DCE=∠ABC;(2)、若OA=3,AC=2,求线段CD的长.24. 某商场的运动服装专柜,对两种品牌的运动服分两次采购试销后,效益可观,计划继续采购进行销售.已知这两种服装过去两次的进货情况如下表.第一次
第二次
品牌运动服装数/件
20
30
品牌运动服装数/件
30
40
累计采购款/元
10200
14400
(1)、问两种品牌运动服的进货单价各是多少元?(2)、由于品牌运动服的销量明显好于品牌,商家决定采购品牌的件数比品牌件数的倍多5件,在采购总价不超过21300元的情况下,最多能购进多少件品牌运动服?25. 一次函数y=kx+b的图象与x轴交于A(﹣2,0),图象过点B(4,n),BC⊥x轴于点C,已知tanB=2,y=kx+b与反比例函数y(x>0)的图象交于点E(a,2),点P是线段AB边上的动点. (1)、分别求直线AB的解析式和反比例函数的解析式;(2)、连接OD,OE,求的值;(3)、是否存在点P,使得△BCP与△BDE相似?若存在,求出此时点P的坐标;若不存在,请说明理由.26. 在等边△ABC的两边AB、AC所在直线上分别有两点M、N,D为△ABC外一点,且∠MDN=60°,∠BDC=120°,BD=DC.探究:当M、N分别在直线AB、AC上移动时,BM、NC、MN之间的数量关系.
(1)、分别求直线AB的解析式和反比例函数的解析式;(2)、连接OD,OE,求的值;(3)、是否存在点P,使得△BCP与△BDE相似?若存在,求出此时点P的坐标;若不存在,请说明理由.26. 在等边△ABC的两边AB、AC所在直线上分别有两点M、N,D为△ABC外一点,且∠MDN=60°,∠BDC=120°,BD=DC.探究:当M、N分别在直线AB、AC上移动时,BM、NC、MN之间的数量关系. (1)、如图1,当点M、N边AB、AC上,且DM=DN时,BM、NC、MN之间的数量关系是;(2)、如图2,点M、N在边AB、AC上,且当DM≠DN时,猜想(1)问的结论还成立吗?若成立请直接写出你的结论;若不成立请说明理由.(3)、如图3,当M、N分别在边AB、CA的延长线上时,探索BM、NC、MN之间的数量关系如何?并给出证明.27. 如图,已知点A(﹣1,0),点B在y轴正半轴上,将Rt△AOB绕点O顺时针旋90°,得到Rt△COD,连接BD,二次函数y=ax2+bx+3的图象过点A,B,D,顶点为E.
(1)、如图1,当点M、N边AB、AC上,且DM=DN时,BM、NC、MN之间的数量关系是;(2)、如图2,点M、N在边AB、AC上,且当DM≠DN时,猜想(1)问的结论还成立吗?若成立请直接写出你的结论;若不成立请说明理由.(3)、如图3,当M、N分别在边AB、CA的延长线上时,探索BM、NC、MN之间的数量关系如何?并给出证明.27. 如图,已知点A(﹣1,0),点B在y轴正半轴上,将Rt△AOB绕点O顺时针旋90°,得到Rt△COD,连接BD,二次函数y=ax2+bx+3的图象过点A,B,D,顶点为E. (1)、求抛物线的表达式;(2)、连接BE,DE,判断△BDE的形状,并求tan∠BDE的值;(3)、在第二象限内有一动点P,使得∠APB=∠EDC,连接DP,线段DP是否存在最大值?如果存在,请求出最大值,如果不存在,请说明理由.
(1)、求抛物线的表达式;(2)、连接BE,DE,判断△BDE的形状,并求tan∠BDE的值;(3)、在第二象限内有一动点P,使得∠APB=∠EDC,连接DP,线段DP是否存在最大值?如果存在,请求出最大值,如果不存在,请说明理由.