山东省济南市济阳区2022年数学一模试题

试卷更新日期：2022-05-26 类型：中考模拟

进入出卷网下载

一、单选题

1. ﹣5的倒数是（）

A、 $- \frac{1}{5}$ B、 $\frac{1}{5}$ C、5 D、﹣5

查看试题解析
2. 下图中几何体的主视图是（）

A、 B、 C、 D、

查看试题解析
3. 某地区计划到2025年建成64700000亩高标准农田，其中64700000用科学记数法表示为（）

A、 $6.47 \times 1 0^{8}$ B、 $0.647 \times 1 0^{8}$ C、 $647 \times 1 0^{5}$ D、 $6.47 \times 1 0^{7}$

查看试题解析
4. 如图，已知AB//CD，DE⊥AC，垂足为E，∠D=20°，则∠A的度数为（）

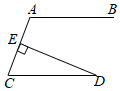A、90° B、100° C、110° D、120°

查看试题解析
5. 以下图案，其中既是轴对称图形又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
6. 下列计算正确的是（　　）

A、2a²+4a²=6a⁴ B、（a+1）²=a²+1 C、（a²）³=a⁵ D、x⁷÷x⁵=x²

查看试题解析
7. 化简 $\frac{m - 1}{m} \div \frac{m^{2} - 1}{m^{2}}$ 的结果是（）

A、 $\frac{m}{m + 1}$ B、 $\frac{1}{m - 1}$ C、 $\frac{m}{m - 1}$ D、 $m$

查看试题解析
8. 某学校在手抄报活动中，济济和洋洋分别从抗击疫情，缅怀先烈，预防溺水三个专题中随机选择一个参加，两人恰好选择同一专题的概率是（）

A、 $\frac{1}{3}$ B、 $\frac{2}{3}$ C、 $\frac{1}{9}$ D、 $\frac{2}{9}$

查看试题解析
9. 函数 $y = \frac{k}{x} (k \neq 0)$ 与函数y= $-$ kx+k在同一坐标系中的图象可能是（）

A、 B、 C、 D、

查看试题解析
10. 如图，热气球的探测器显示，从热气球A处看一栋楼顶部B处的仰角为36°，看这栋楼底部C处的俯角为60°，热气球A处与楼的水平距离为100m，则这栋楼的高度为（）（参考数据： $\sqrt{3}$ ≈1.73，tan36°≈0.73，sin36°≈0.59，cos36°≈0.81，结果保留整数）

A、232 m B、246 m C、254 m D、310 m

查看试题解析
11. 如图，在△ABC中，AB＝AC．在AB、AC上分别截取AP、AQ，使AP＝AQ．再分别以点P，Q为圆心，以大于 $\frac{1}{2}$ PQ的长为半径作弧，两弧在∠BAC内交于点R，作射线AR，交BC于点D．已知BC＝5，AD=6．若点M、N分别是线段AD和线段AC上的动点，则CM+MN的最小值为（）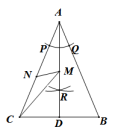

A、4 B、5 C、 $\frac{60}{13}$ D、2 $\sqrt{6}$

查看试题解析
12. 若二次函数y=a $x^{2}$ +bx+c（a≠0）的图象的顶点在第二象限，且过点（0，1）和（1，0），则m=a-b+c的值的变化范围是（）

A、0<m<1 B、0<m<2 C、1<m<2 D、-1<m<1

查看试题解析

二、填空题

13. 因式分解：a²﹣6a+9= ．

查看试题解析
14. 在一次以“建设美丽济阳”为主题的演讲比赛中，小红的演讲内容、语言表达、演讲技能、形象礼仪的各项得分依次为9.5；9.4；9.2；9.7．若依次按40%，25%，25%， $10 %$ 的比例确定她的综合得分，则她的综合得分是．

查看试题解析
15. 如图，正五边形ABCDE中，内角∠EAB的角平分线与其内角∠ABC的角平分线相交于点P，则∠APB＝度．

查看试题解析
16. 已知关于x的一元二次方程ax²﹣2x+c=0有两个相等的实数根，则 $\frac{1}{a}$ ﹣c+1的值等于．

查看试题解析
17. 甲、乙两施工队分别从两端修一段长度为315米的公路．在施工过程中，甲队曾因技术改进而停工一天，之后加快了施工进度并与乙队共同按期完成任务．下表根据每天工程进度制作而成的．
施工时间/天
1
2
3
4
5
6
7
8
9
10
累计完成施工量/米
25
50
75
100
115
155
195
235
275
315
甲队技术改进后比技术改进前每天多修路米．

查看试题解析
18. 如图，△ABC中，∠ABC=90^° ， AB=2，BC=4，点D是斜边AC的中点，将△DBC沿直线BD对折，C点落在E处，连接AE，则AE的长度为．

查看试题解析

三、解答题

19. 计算： ${(\frac{1}{3})}^{- 1} - 2 \cos 30 ° + | - \sqrt{3} | - {(4 - π)}^{0}$ ．

查看试题解析
20. 解不等式组 ${\begin{array}{l} x + 4 \leq 3 (x + 2) \\ \frac{x - 1}{2} < \frac{x}{3} \end{array}$ ，并写出它的所有整数解

查看试题解析
21. 如图，已知四边形ABCD是平行四边形，BE⊥AC， DF⊥AC，求证：AE＝CF．

查看试题解析

22. 某校举行了冬奥会知识竞赛，在全校随机抽取了部分学生的竞赛成绩进行整理和分析（成绩得分用x表示，共分成四组），并绘制成如下的竞赛成绩分组统计表和扇形统计图．其中“60≤x＜80”这组的数据如下：

61，74，68，62，73，70，72，78，69，74，79，68，74．

竞赛成绩分组统计表
组别	竞赛成绩分组	频数
1	60 $\leq$ x<70	a
2	70 $\leq$ x<80	b
3	80 $\leq$ x<90	12
4	90 $\leq$ x $\leq$ 100	d

竞赛成绩扇形统计图

请根据以上信息，解答下列问题：

(1)、填空：a=；

(2)、统计图中第四组对应圆心角为度；

(3)、“70≤x＜80”这组数据的众数是，中位数是；

(4)、若学生竞赛成绩达到90分及以上获奖，请你估计全校1200名学生中获奖的人数．

查看试题解析

23. 如图，在△ABC中， $A B = A C$ ，以AB为直径的 $⊙ O$ 分别交AC，BC于点D，E，过B点的圆的切线交AC的延长线于点F．

(1)、求证：∠FBC= $\frac{1}{2}$ ∠BAC；

(2)、若 $t a n ∠ B F A = \frac{3}{4}$ ， AD=6，求 $⊙ O$ 的半径的长．

查看试题解析
24. 某超市共用24000元同时购进甲、乙两种型号书包各200个，购进甲型号书包40个比购进乙型书包30个少用100元．

(1)、求甲、乙两种型号书包的进价各为多少元?

(2)、若超市把甲、乙两种型号书包均按每个90元定价进行零售，同时为扩大销售，拿出一部分书包按零售价的8折进行优惠销售．商场在这批背包全部售完后，若总获利不低于10200元，则超市用于优惠销售的书包数量最多为多少个?

查看试题解析
25. 如图，四边形AOBC是的正方形，D为BC中点，以O为坐标原点，OA，OB所在的直线为坐标轴建立平面直角坐标系，A点坐标（0，4），过点D的反比例函数y＝ $\frac{k}{x}$ （k≠0）的图象与边AC交于E点，F是线段OB上的一动点．
备用图

(1)、求k的值并直接写出点E的坐标；

(2)、若AD平分∠CAF，求出F点的坐标；

(3)、若△AFD的面积为S₁ ， △AFO的面积为S₂ ．若S₁：S₂=3：2，判断四边形AEFO的形状．并说明理由．

查看试题解析
26. 在直角△ABC中，∠ACB=90^° ， AC=3，BC=4，点D、E和F分别是斜边AB、直角边AC和直角边BC上的动点，∠EDF=90°，

(1)、如图1，若四边形DECF是正方形，求这个正方形的边长．

(2)、如图2，若E点正好运动到C点，并且tan∠DCF= $\frac{1}{2}$ ，求BF的长．

(3)、如图3，当 $\frac{D E}{D F} = \frac{1}{2}$ 时，求 $\frac{A D}{D B}$ 的值

查看试题解析
27. 抛物线 $y = a x^{2} + b x - 3$ 过点A（－1，0），点B（3，0），与y轴交于C点．

(1)、求抛物线的表达式及点C的坐标；

(2)、如图1，设M是抛物线上的一点，若∠MAB=45°，求M点的坐标；

(3)、如图2，点P在直线BC下方的抛物线上，过点P作PD⊥x轴于点D，交直线BC于点E，过P点作PF⊥BC，交BC与F点，△PEF的周长是否有最大值，若有最大值，求出此时P点的坐标．若不存在，说明理由．

查看试题解析

施工时间/天	1	2	3	4	5	6	7	8	9	10
累计完成施工量/米	25	50	75	100	115	155	195	235	275	315