山东省菏泽市牡丹区2022年中考一模数学试题
试卷更新日期:2022-05-26 类型:中考模拟
一、单选题
-
1. 下列实数中,无理数是( )A、 B、 C、 D、-12. 近年来,新冠肺炎给人类带来了巨大灾难,经科学家研究,冠状病毒多数为球形或近似球形,其直径约为0.00000011米,其中数据0.00000011用科学记数法表示正确的是( )A、 B、 C、 D、3. 冬奥会于2022年2月4日在中国北京、张家口等地召开,并在此之前进行了冬奥会会标征集活动,以下是部分参选作品,其文字上方的图案是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 4. 函数 中自变量x的取值范围是( )A、 B、 或 C、 D、 且5. 如图,在已知的中,按以下步骤作图:①分别以B,C为圆心,以大于的长为半径作弧,两弧相交于两点M,N;②作直线MN交AB于点D,连接CD.若 , , 则∠ACB的度数为( )
4. 函数 中自变量x的取值范围是( )A、 B、 或 C、 D、 且5. 如图,在已知的中,按以下步骤作图:①分别以B,C为圆心,以大于的长为半径作弧,两弧相交于两点M,N;②作直线MN交AB于点D,连接CD.若 , , 则∠ACB的度数为( )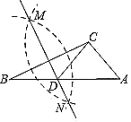 A、105° B、100° C、95° D、90°6. 老师设计了接力游戏,用合作的方式完成“求抛物线 的顶点坐标”,规则如下:每人只能看到前一人给的式子,并进行一步计算,再将结果传递给下一人,最后完成解答.过程如图所示:
A、105° B、100° C、95° D、90°6. 老师设计了接力游戏,用合作的方式完成“求抛物线 的顶点坐标”,规则如下:每人只能看到前一人给的式子,并进行一步计算,再将结果传递给下一人,最后完成解答.过程如图所示:
接力中,自己负责的一步出现错误的是( )
A、只有丁 B、乙和丁 C、乙和丙 D、甲和丁7. 如图,已知△ABC与△DEF位似,位似中心为点O,且△ABC的面积等于△DEF面积的 ,则AO:AD的值为( )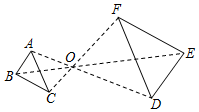 A、2:3 B、2:5 C、4:9 D、4:138. 如图,在四边形DEFG中,∠E=∠F=90°,∠DGF=45°,DE=1,FG=3,Rt△ABC的直角顶点C与点G重合,另一个顶点B(在点C左侧)在射线FG上,且BC=1,AC=2,将△ABC沿GF方向平移,点C与点F重合时停止.设CG的长为x , △ABC在平移过程中与四边形DEFG重叠部分的面积为y , 则下列图象能正确反映y与x函数关系的是( )
A、2:3 B、2:5 C、4:9 D、4:138. 如图,在四边形DEFG中,∠E=∠F=90°,∠DGF=45°,DE=1,FG=3,Rt△ABC的直角顶点C与点G重合,另一个顶点B(在点C左侧)在射线FG上,且BC=1,AC=2,将△ABC沿GF方向平移,点C与点F重合时停止.设CG的长为x , △ABC在平移过程中与四边形DEFG重叠部分的面积为y , 则下列图象能正确反映y与x函数关系的是( )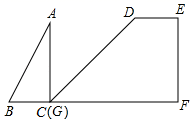 A、
A、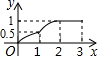 B、
B、 C、
C、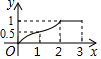 D、
D、
二、填空题
-
9. 把多项式9m2﹣36n2分解因式的结果是 .10. 若关于x的分式方程 的解为正数,则a的取值范围 .11. 如图,在△ABC中,∠ACB=90°,CD=2,以CD为直径的⊙与AB相切于点E.若弧DE的长为为 π,则阴影部分的面积为 .(保留π)
 12. 定义:如果一元二次方程()满足 , 那么我们称这个方程为“凤凰”方程.已知是“凤凰”方程,且有两个相等的实数根,则 .13. 如图,在平面直角坐标系中,矩形OABC的顶点A、C分别在x轴的负半轴、y轴的正半轴上,点B在第二象限.将矩形OABC绕点O顺时针旋转,使点B落在y轴上,得到矩形ODEF,BC与OD相交于点M.若经过点M的反比例函数y=
12. 定义:如果一元二次方程()满足 , 那么我们称这个方程为“凤凰”方程.已知是“凤凰”方程,且有两个相等的实数根,则 .13. 如图,在平面直角坐标系中,矩形OABC的顶点A、C分别在x轴的负半轴、y轴的正半轴上,点B在第二象限.将矩形OABC绕点O顺时针旋转,使点B落在y轴上,得到矩形ODEF,BC与OD相交于点M.若经过点M的反比例函数y= (x<0)的图象交AB于点N,的图象交AB于点N, S矩形OABC=32,tan∠DOE=
(x<0)的图象交AB于点N,的图象交AB于点N, S矩形OABC=32,tan∠DOE= , 则BN的长为.
, 则BN的长为. 14. 如图,在正方形ABCD中,O是对角线AC与BD的交点,M是BC边上的动点(点M不与点B,C重合),过点C作CN⊥DM交AB于点N,连接OM、ON,MN.下列五个结论:①△CNB≌△DMC;②ON=OM;③ON⊥OM;④若AB=2,则S△OMN的最小值是1;⑤AN2+CM2=MN2 . 其中正确结论是 . (只填序号)
14. 如图,在正方形ABCD中,O是对角线AC与BD的交点,M是BC边上的动点(点M不与点B,C重合),过点C作CN⊥DM交AB于点N,连接OM、ON,MN.下列五个结论:①△CNB≌△DMC;②ON=OM;③ON⊥OM;④若AB=2,则S△OMN的最小值是1;⑤AN2+CM2=MN2 . 其中正确结论是 . (只填序号)
三、解答题
-
15. 计算:16. 先化简,再求值: ,其中a的值从不等式组 的解集中选取一个合适的整数.17. 如图,在菱形ABCD中,点E,F分别是边AD,AB的中点.
 (1)、求证:△ABE≌△ADF;(2)、若BE= ,∠C=60°,求菱形ABCD的面积.18. 如图,在高度为100米的小山上竖直建有一座铁塔,小明为测得铁塔的高度,先在山脚C处测得铁塔底部B的仰角为30°,后沿坡度i=1:的山坡向上行走米到达点D处,在点D处测得铁塔顶部A的仰角为30°,求铁塔AB的高度.
(1)、求证:△ABE≌△ADF;(2)、若BE= ,∠C=60°,求菱形ABCD的面积.18. 如图,在高度为100米的小山上竖直建有一座铁塔,小明为测得铁塔的高度,先在山脚C处测得铁塔底部B的仰角为30°,后沿坡度i=1:的山坡向上行走米到达点D处,在点D处测得铁塔顶部A的仰角为30°,求铁塔AB的高度. 19. 为响应政府发出的创建文明城市的号召,我市计划用两种花卉对某广场进行美化.已知用800元购买A种花卉与用1200元购买B种花卉的数量相等,且B种花卉每盆比A种花卉多1.5元.(1)、求A、B两种花卉每盆各多少元?(2)、计划购买A、B两种花卉共8000盆,其中A种花卉的数量不超过B种花卉数量的 , 求购买A种花卉多少盆时,购买这批花卉总费用最低,最低费用是多少元?20. 如图一次函数y=k1x+3的图象与坐标轴相交于点A(﹣2,0)和点B,与反比例函数y= (x>0)相交于点C(2,m).
19. 为响应政府发出的创建文明城市的号召,我市计划用两种花卉对某广场进行美化.已知用800元购买A种花卉与用1200元购买B种花卉的数量相等,且B种花卉每盆比A种花卉多1.5元.(1)、求A、B两种花卉每盆各多少元?(2)、计划购买A、B两种花卉共8000盆,其中A种花卉的数量不超过B种花卉数量的 , 求购买A种花卉多少盆时,购买这批花卉总费用最低,最低费用是多少元?20. 如图一次函数y=k1x+3的图象与坐标轴相交于点A(﹣2,0)和点B,与反比例函数y= (x>0)相交于点C(2,m). (1)、求出一次函数与反比例函数的解析式;(2)、若点P是反比例函数图象上的一点,连接CP并延长,交x轴正半轴于点D,若PD:CP=1:2时,求△COP的面积.21. 为了丰富学生们的课余生活,学校准备开展第二课堂,有四类课程可供选择,分别是“A.书画类、B.文艺类、C.社会实践类、D.体育类”.现随机抽取了七年级部分学生对报名意向进行调查,并根据调查结果绘制了两幅不完整的统计图,请你根据图表信息回答下列问题:
(1)、求出一次函数与反比例函数的解析式;(2)、若点P是反比例函数图象上的一点,连接CP并延长,交x轴正半轴于点D,若PD:CP=1:2时,求△COP的面积.21. 为了丰富学生们的课余生活,学校准备开展第二课堂,有四类课程可供选择,分别是“A.书画类、B.文艺类、C.社会实践类、D.体育类”.现随机抽取了七年级部分学生对报名意向进行调查,并根据调查结果绘制了两幅不完整的统计图,请你根据图表信息回答下列问题: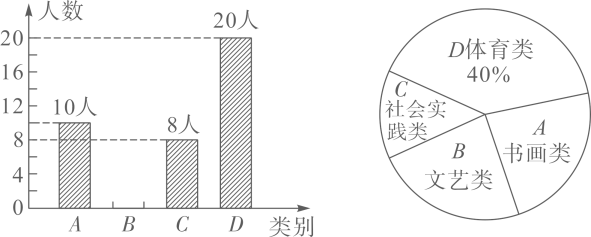 (1)、本次被抽查的学生共有名,扇形统计图中“A.书画类”所占扇形的圆心角的度数为度;(2)、请你将条形统计图补全;(3)、若该校七年级共有600名学生,请根据上述调查结果估计该校学生选择“C.社会实践类”的学生共有多少名?(4)、本次调查中抽中了七(1)班王芳和小颖两名学生,请用列表法或画树状图法求她们选择同一个项目的概率.22. 如图,四边形ABCD内接于⊙O,∠BAD=90°,AD、BC的延长线交于点F,点E在CF上,且∠DEC=∠BAC.
(1)、本次被抽查的学生共有名,扇形统计图中“A.书画类”所占扇形的圆心角的度数为度;(2)、请你将条形统计图补全;(3)、若该校七年级共有600名学生,请根据上述调查结果估计该校学生选择“C.社会实践类”的学生共有多少名?(4)、本次调查中抽中了七(1)班王芳和小颖两名学生,请用列表法或画树状图法求她们选择同一个项目的概率.22. 如图,四边形ABCD内接于⊙O,∠BAD=90°,AD、BC的延长线交于点F,点E在CF上,且∠DEC=∠BAC. (1)、求证:DE是⊙O的切线;(2)、当AB=AC时,若CE=4,EF=6,求⊙O的半径.23. 如图1,Rt△ABC中,∠C=90°,点E是AB边上一点,且点E不与A、B重合,ED⊥AC于点D.
(1)、求证:DE是⊙O的切线;(2)、当AB=AC时,若CE=4,EF=6,求⊙O的半径.23. 如图1,Rt△ABC中,∠C=90°,点E是AB边上一点,且点E不与A、B重合,ED⊥AC于点D. (1)、当sinB=时,
(1)、当sinB=时,①求证:BE=2CD;
②当△ADE绕点A旋转到如图2的位置时(60°<∠CAD<90°),BE=2CD是否成立?若成立,请给出证明;若不成立,请说明理由.
(2)、当sinB=时,将△ADE绕点A旋转到∠DEB=90°,若AC=10,AD=2 , 请直接写出线段CD的长.24. 如图,抛物线y=ax2+ x+c与x轴交于点A,B,与y轴交于点C,已知A,C两点坐标分别是A(1,0),C(0,﹣2),连接AC,BC. (1)、求抛物线的表达式和AC所在直线的表达式;(2)、将 ABC沿BC所在直线折叠,得到 DBC,点A的对应点D是否落在抛物线的对称轴上,若点D在对称轴上,请求出点D的坐标;若点D不在对称轴上,请说明理由;(3)、若点P是抛物线位于第三象限图象上的一动点,连接AP交BC于点Q,连接BP, BPQ的面积记为S1 , ABQ的面积记为S2 , 求 的值最大时点P的坐标.
(1)、求抛物线的表达式和AC所在直线的表达式;(2)、将 ABC沿BC所在直线折叠,得到 DBC,点A的对应点D是否落在抛物线的对称轴上,若点D在对称轴上,请求出点D的坐标;若点D不在对称轴上,请说明理由;(3)、若点P是抛物线位于第三象限图象上的一动点,连接AP交BC于点Q,连接BP, BPQ的面积记为S1 , ABQ的面积记为S2 , 求 的值最大时点P的坐标.