山东省德州市宁津县2022年中考一模数学试题
试卷更新日期:2022-05-26 类型:中考模拟
一、单选题
-
1. -2的相反数是( )A、2 B、-2 C、 D、2. 截至2021年11月2日,中国神舟十三号载人飞船长征二号已在轨飞行18天,距离地球约63800000千米,用科学记数法表示63800000千米为( )A、千米 B、千米 C、千米 D、千米3. 下列四个几何体中,俯视图形状与其它三个不同的是( )A、
 B、
B、 C、
C、 D、
D、 4. 下列运算正确的是( )A、 B、 C、 D、5. 高尔基说:“书,是人类进步的阶梯”.阅读可以丰富知识,拓展视野,充实生活,给我们带来愉快.英才中学计划在各班设立图书角,为合理搭配各类书籍,学校团委以“我最喜爱的书籍”为主题,对全校学生进行抽样调查,收集整理喜爱的书籍类型(A.科普,B.文学,C.体育,D.其他)数据后,绘制出两幅不完整的统计图,则下列说法错误的是( )
4. 下列运算正确的是( )A、 B、 C、 D、5. 高尔基说:“书,是人类进步的阶梯”.阅读可以丰富知识,拓展视野,充实生活,给我们带来愉快.英才中学计划在各班设立图书角,为合理搭配各类书籍,学校团委以“我最喜爱的书籍”为主题,对全校学生进行抽样调查,收集整理喜爱的书籍类型(A.科普,B.文学,C.体育,D.其他)数据后,绘制出两幅不完整的统计图,则下列说法错误的是( )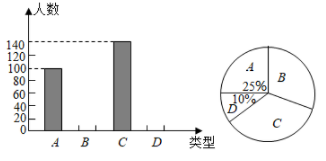 A、样本容量为400 B、类型D所对应的扇形的圆心角为 C、类型C所占百分比为 D、类型B的人数为120人6. 把不等式组 中每个不等式的解集在同一条数轴上表示出来,正确的为( )A、
A、样本容量为400 B、类型D所对应的扇形的圆心角为 C、类型C所占百分比为 D、类型B的人数为120人6. 把不等式组 中每个不等式的解集在同一条数轴上表示出来,正确的为( )A、 B、
B、 C、
C、 D、
D、 7. 如图,与正五边形的两边 , 相切于A,C两点,则的度数是( )
7. 如图,与正五边形的两边 , 相切于A,C两点,则的度数是( ) A、 B、 C、 D、8. 若二次函数的图象如图所示,则一次函数与反比例函数在同一个坐标系内的大致图象为( )
A、 B、 C、 D、8. 若二次函数的图象如图所示,则一次函数与反比例函数在同一个坐标系内的大致图象为( )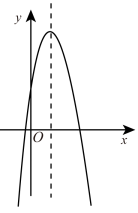 A、
A、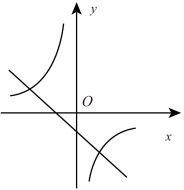 B、
B、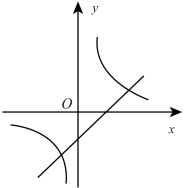 C、
C、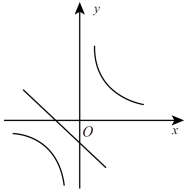 D、
D、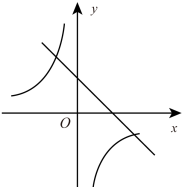 9. 随着电影《你好,李焕英》热映,其同名小说的销量也急剧上升.某书店分别用400元和600元两次购进该小说,第二次数量比第一次多1倍,且第二次比第一次进价便宜4元,设书店第一次购进x套,根据题意,下列方程正确的是( )A、 B、 C、 D、10. 如图,在一次数学实践活动中,小明同学要测量一座与地面垂直的古塔 的高度,他从古塔底部点B处前行 到达斜坡 的底部点C处,然后沿斜坡 前行 到达最佳测量点D处,在点D处测得塔顶A的仰角为 ,已知斜坡的斜面坡度 ,且点A,B,C,D,E在同一平面内,小明同学测得古塔 的高度是( )
9. 随着电影《你好,李焕英》热映,其同名小说的销量也急剧上升.某书店分别用400元和600元两次购进该小说,第二次数量比第一次多1倍,且第二次比第一次进价便宜4元,设书店第一次购进x套,根据题意,下列方程正确的是( )A、 B、 C、 D、10. 如图,在一次数学实践活动中,小明同学要测量一座与地面垂直的古塔 的高度,他从古塔底部点B处前行 到达斜坡 的底部点C处,然后沿斜坡 前行 到达最佳测量点D处,在点D处测得塔顶A的仰角为 ,已知斜坡的斜面坡度 ,且点A,B,C,D,E在同一平面内,小明同学测得古塔 的高度是( ) A、 B、 C、 D、11. 如图,在矩形中, , , 以点B为圆心、的长为半径画弧交于点E,再分别以点C,E为圆心、大于的长为半径画弧,两弧交于点F,作射线交于点G,则的长为( )
A、 B、 C、 D、11. 如图,在矩形中, , , 以点B为圆心、的长为半径画弧交于点E,再分别以点C,E为圆心、大于的长为半径画弧,两弧交于点F,作射线交于点G,则的长为( )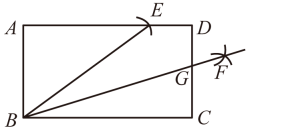 A、2 B、 C、3 D、12. 如图,点A是x轴上一个定点,点B从原点O出发沿y轴的正方向移动,以线段为边在y轴右侧作C等边三角形 , 以线段为边在上方作等边三角形 , 连接 , 随点B的移动,下列四个结论;①;②直线与x轴所夹的锐角恒为;③;④随点B的移动,线段的长逐渐增大.其中正确结论的个数为( )
A、2 B、 C、3 D、12. 如图,点A是x轴上一个定点,点B从原点O出发沿y轴的正方向移动,以线段为边在y轴右侧作C等边三角形 , 以线段为边在上方作等边三角形 , 连接 , 随点B的移动,下列四个结论;①;②直线与x轴所夹的锐角恒为;③;④随点B的移动,线段的长逐渐增大.其中正确结论的个数为( )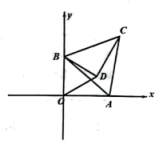 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
13. 若式子 在实数范围内有意义,则x的取值范围是 .
14. 已知关于的一元二次方程的一个根是2.则另一个根是 .15. 数学活动课上,小明同学尝试将正方形纸片剪去一个小正方形,剩余部分沿虚线剪开,拼成新的图形。现给出下列3种不同的剪、拼方案,其中能够验证平方差公式的方案是 。(请填上正确的序号) 16. ⊙P过坐标原点O,与x轴、y轴相交于点A、B,且OA=OB=4,反比例函数的图象经过圆点P,作射线OP,则图中阴影部分面积为
16. ⊙P过坐标原点O,与x轴、y轴相交于点A、B,且OA=OB=4,反比例函数的图象经过圆点P,作射线OP,则图中阴影部分面积为 17. 如图,一次函数的图象为直线l,菱形 , , …按图中所示的方式放置,顶点A, , , , …均在直线l上,顶点 , , …均在x轴上,则点的纵坐标是 .
17. 如图,一次函数的图象为直线l,菱形 , , …按图中所示的方式放置,顶点A, , , , …均在直线l上,顶点 , , …均在x轴上,则点的纵坐标是 . 18. 已知:点E是正方形ABCD边上的一点,将线段AE绕点E顺时针旋转90°,得到线段EA′,若AB=2,则线段DA′的最小值为
18. 已知:点E是正方形ABCD边上的一点,将线段AE绕点E顺时针旋转90°,得到线段EA′,若AB=2,则线段DA′的最小值为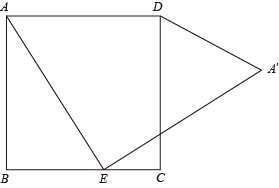
三、解答题
-
19. 先化简,再求值: , 其中20. 某校七、八年级各有500名学生,为了解该校七、八年级学生对党史知识的掌握情况,从七、八年级学生中各随机抽取15人进行党史知识测试,统计这部分学生的测试成绩(成绩均为整数,满分10分,8分及以上为优秀),相关数据统计、整理如下:七年级抽取学生的成绩:6,6,6,8,8,8,8,8,8,8,9,9,9,9,10;
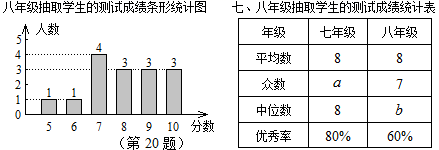 (1)、填空: = , =;(2)、根据以上数据,你认为该校七、八年级中,哪个年级的学生党史知识掌握得较好?请说明理由(写出一条即可);(3)、请估计七、八年级学生对党史知识掌握能够达到优秀的总人数;(4)、现从七、八年级获得10分的4名学生中随机抽取2人参加市党史知识竞赛,请用列表或画树状图法,求出被选中的2人恰好是七、八年级各1人的概率.21. 九年级某数学兴趣小组在学习了反比例函数的图象与性质后,进一步研究了函数的图象与性质,其探究过程如下:
(1)、填空: = , =;(2)、根据以上数据,你认为该校七、八年级中,哪个年级的学生党史知识掌握得较好?请说明理由(写出一条即可);(3)、请估计七、八年级学生对党史知识掌握能够达到优秀的总人数;(4)、现从七、八年级获得10分的4名学生中随机抽取2人参加市党史知识竞赛,请用列表或画树状图法,求出被选中的2人恰好是七、八年级各1人的概率.21. 九年级某数学兴趣小组在学习了反比例函数的图象与性质后,进一步研究了函数的图象与性质,其探究过程如下: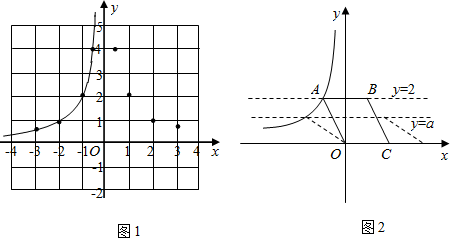 (1)、绘制函数图象,如图1.
(1)、绘制函数图象,如图1.列表:下表是与的几组对应值,其中;
1
2
3
1
2
4
4
2
描点:根据表中各组对应值 , 在平面直角坐标系中描出了各点;
连线:用平滑的曲线顺次连接各点,画出了部分图象.请你把图象补充完整;
(2)、通过观察图1,写出该函数的两条性质;①;
②;
(3)、①观察发现:如图2.若直线交函数的图象于A,B两点,连接 , 过点作交轴于 . 则S四边形OABC=;②探究思考:将①中“直线”改为“直线”,其他条件不变,则S四边形OABC=;
③类比猜想:若直线交函数的图象于A,B两点,连接 , 过点作交轴于 , 则 .
22. 如图,AB为⊙O的直径,C为BA延长线上一点,D为⊙O上一点,OF⊥AD于点E,交CD于点F,且∠ADC=∠AOF.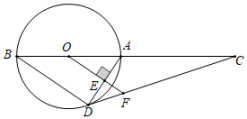 (1)、求证:CD与⊙O相切于点D;(2)、若sin∠C= , BD=12,求EF的长.23. 某商场购进A、B两种商品进行销售,已知购进4件A商品和6件B商品需260元,购进5件A商品和4件B商品需220元.两种商品以相同的售价销售,A商品的销售量(件)与售价x(元)之间的关系为;当售价为40元时,B商品可销售100件,售价每提高1元,少销售3件.(1)、求A、B两种商品每件的进价分别为多少元?(2)、当商品售价为多少元时,A、B两种商品的销售利润总和最大?最大利润是多少?
(1)、求证:CD与⊙O相切于点D;(2)、若sin∠C= , BD=12,求EF的长.23. 某商场购进A、B两种商品进行销售,已知购进4件A商品和6件B商品需260元,购进5件A商品和4件B商品需220元.两种商品以相同的售价销售,A商品的销售量(件)与售价x(元)之间的关系为;当售价为40元时,B商品可销售100件,售价每提高1元,少销售3件.(1)、求A、B两种商品每件的进价分别为多少元?(2)、当商品售价为多少元时,A、B两种商品的销售利润总和最大?最大利润是多少?

