山东省德州市陵城区2022年九年级下学期第一次练兵考试数学试题
试卷更新日期:2022-05-26 类型:中考模拟
一、单选题
-
1. 下列四个数中,最小的数是( )A、 B、 C、 D、02. 围棋起源于中国,古代称之为“弈”,至今已有四千多年的历史.下列由黑白棋子摆成的图案是轴对称图形的是( )A、
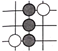 B、
B、 C、
C、 D、
D、 3. 下列计算正确的是( )A、 B、 C、 D、4. 如图2是图1长方体的三视图,若用S表示面积, ,则 ( )
3. 下列计算正确的是( )A、 B、 C、 D、4. 如图2是图1长方体的三视图,若用S表示面积, ,则 ( )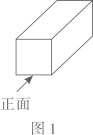
 A、 B、 C、 D、5. 如图,Rt△ABC中,∠C=90°,利用尺规在BC、BA上分别截取BE、BD,使BE=BD;分别以D、E为圆心,以大于DE长为半径作弧,两弧在∠CBA内交于点F;作射线BF交AC于点H,若CH=2,P为AB上一动点,则HP的最小值为( )
A、 B、 C、 D、5. 如图,Rt△ABC中,∠C=90°,利用尺规在BC、BA上分别截取BE、BD,使BE=BD;分别以D、E为圆心,以大于DE长为半径作弧,两弧在∠CBA内交于点F;作射线BF交AC于点H,若CH=2,P为AB上一动点,则HP的最小值为( ) A、 B、1 C、2 D、无法确定6. 某篮球队16名队员的年龄情况如下表,则这些队员年龄的众数和中位数分别是( )
A、 B、1 C、2 D、无法确定6. 某篮球队16名队员的年龄情况如下表,则这些队员年龄的众数和中位数分别是( )年龄(单位:岁)
14
15
16
17
18
人数
3
3
5
3
2
A、16,17 B、16,16 C、16,16.5 D、3,177. 二次函数y=ax2+bx+c的图象如图所示,则反比例函数y=与一次函数y=bx+c在同一坐标系内的大致图象是( ) A、
A、 B、
B、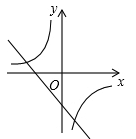 C、
C、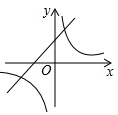 D、
D、 8. 已知关于x的不等式组 恰有4个整数解,则a的取值范围是( )A、﹣1<a<﹣ B、﹣1≤a≤﹣ C、﹣1<a≤﹣ D、﹣1≤a<﹣9. 圆的一条弦把圆分为度数比为的两条弧,则弦心距与弦长的比为( )A、 B、 C、 D、10. 勾股定理是人类最伟大的科学发现之一,在我国古算书《周髀算经》中早有记载.如图1,以直角三角形的各边为边分别向外作正方形,再将较小的两个正方形分别绕直角三角形斜边上的两顶点旋转得到图2.则图2中阴影部分面积等于( )
8. 已知关于x的不等式组 恰有4个整数解,则a的取值范围是( )A、﹣1<a<﹣ B、﹣1≤a≤﹣ C、﹣1<a≤﹣ D、﹣1≤a<﹣9. 圆的一条弦把圆分为度数比为的两条弧,则弦心距与弦长的比为( )A、 B、 C、 D、10. 勾股定理是人类最伟大的科学发现之一,在我国古算书《周髀算经》中早有记载.如图1,以直角三角形的各边为边分别向外作正方形,再将较小的两个正方形分别绕直角三角形斜边上的两顶点旋转得到图2.则图2中阴影部分面积等于( )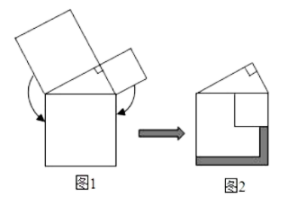 A、直角三角形的面积 B、最大正方形的面积 C、最大正方形与直角三角形的面积和 D、较小两个正方形重叠部分的面积11. 如图,在平面直角坐标系中,双曲线y(k>0)与一直线交于A(﹣2,m)、B(1,n)两点,点H是双曲线第三象限上的动点(在点A右侧),直线AH、BH分别与y轴交于P、Q两点,若HA=a•HP,HB=b•HQ,则a,b的关系式成立的是( )
A、直角三角形的面积 B、最大正方形的面积 C、最大正方形与直角三角形的面积和 D、较小两个正方形重叠部分的面积11. 如图,在平面直角坐标系中,双曲线y(k>0)与一直线交于A(﹣2,m)、B(1,n)两点,点H是双曲线第三象限上的动点(在点A右侧),直线AH、BH分别与y轴交于P、Q两点,若HA=a•HP,HB=b•HQ,则a,b的关系式成立的是( ) A、a+b=2 B、a﹣b=﹣2 C、a+2b=3 D、a﹣2b=﹣312. 如图,正方形 , 点E,F分别在边 , 上, , , 与交于点M,与交于点N,延长至G,使 , 连接 . 有如下结论:①;②;③;④ . 上述结论中,所有正确结论的序号是( )
A、a+b=2 B、a﹣b=﹣2 C、a+2b=3 D、a﹣2b=﹣312. 如图,正方形 , 点E,F分别在边 , 上, , , 与交于点M,与交于点N,延长至G,使 , 连接 . 有如下结论:①;②;③;④ . 上述结论中,所有正确结论的序号是( ) A、①② B、①③ C、①②④ D、②③④
A、①② B、①③ C、①②④ D、②③④二、填空题
-
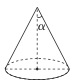
13. 计算的值是.14. 如图,圆锥的底面半径为3,侧面积为 , 设圆锥的母线与高的夹角为 , 则的值是 .
 15. 若关于x的分式方程 ﹣2m= 无解,则m的值为.16. 已知等腰三角形的三边长分别为a、b、4,且a、b是关于x的一元二次方程x2﹣12x+m+2=0的两根,则m的值是 .17. 抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,与x轴的一个交点坐标为(﹣1,0),该抛物线的部分图象如图所示,下列结论:①4ac<b2; ②方程ax2+bx+c=0的两个根是x1=﹣1,x2=3; ③3a+c>0; ④当x<0时,y随x增大而减小;⑤点P(m , n)是抛物线上任意一点,则m(am+b)≤a+b , 其中正确的结论是 .(填写序号)
15. 若关于x的分式方程 ﹣2m= 无解,则m的值为.16. 已知等腰三角形的三边长分别为a、b、4,且a、b是关于x的一元二次方程x2﹣12x+m+2=0的两根,则m的值是 .17. 抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,与x轴的一个交点坐标为(﹣1,0),该抛物线的部分图象如图所示,下列结论:①4ac<b2; ②方程ax2+bx+c=0的两个根是x1=﹣1,x2=3; ③3a+c>0; ④当x<0时,y随x增大而减小;⑤点P(m , n)是抛物线上任意一点,则m(am+b)≤a+b , 其中正确的结论是 .(填写序号) 18. 如图,在平面直角坐标系中,直线与x轴交于点 , 以为一边作正方形 , 使得点在y轴正半轴上,延长交直线l于点 , 按同样方法依次作正方形、正方形…、正方形 , 使得点均在直线l上,点在y轴正半轴上,则点的横坐标是 .
18. 如图,在平面直角坐标系中,直线与x轴交于点 , 以为一边作正方形 , 使得点在y轴正半轴上,延长交直线l于点 , 按同样方法依次作正方形、正方形…、正方形 , 使得点均在直线l上,点在y轴正半轴上,则点的横坐标是 .
三、解答题
-
19. 化简求值:(1)、如图,已知实数、在数抽上的位置如图所示,试化简.
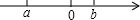 (2)、已知 , , 求代数式的值.20. 学生社团是指学生在自愿基础上结成的各种群众性文化、艺术、学术团体.不分年级、由兴趣爱好相近的同学组成,在保证学生完成学习任务和不影响学校正常教学秩序的前提下开展各种活动.某校就学生对“篮球社团、动漫社团、文学社团和摄影社团”四个社团选择意向进行了抽样调查(每人选报一类),绘制了如图所示的两幅统计图(不完整).
(2)、已知 , , 求代数式的值.20. 学生社团是指学生在自愿基础上结成的各种群众性文化、艺术、学术团体.不分年级、由兴趣爱好相近的同学组成,在保证学生完成学习任务和不影响学校正常教学秩序的前提下开展各种活动.某校就学生对“篮球社团、动漫社团、文学社团和摄影社团”四个社团选择意向进行了抽样调查(每人选报一类),绘制了如图所示的两幅统计图(不完整).请根据图中信息,解答下列问题.
 (1)、求扇形统计图中m= ▲ , 并补全条形统计图;(2)、已知该校有1600名学生,请估计“文学社团”共有多少人?(3)、在“动漫社团”活动中,甲、乙、丙、丁四名同学表现优秀,现决定从这四名同学中任选两名参加“中学生原创动漫大赛”,请用列表或画树状图的方法求出恰好选中乙、丙两位同学的概率.21. 鄂州市某校数学兴趣小组借助无人机测量一条河流的宽度 .如图所示,一架水平飞行的无人机在A处测得正前方河流的左岸C处的俯角为 ,无人机沿水平线 方向继续飞行50米至B处,测得正前方河流右岸D处的俯角为30°.线段 的长为无人机距地面的铅直高度,点M、C、D在同一条直线上.其中 米.
(1)、求扇形统计图中m= ▲ , 并补全条形统计图;(2)、已知该校有1600名学生,请估计“文学社团”共有多少人?(3)、在“动漫社团”活动中,甲、乙、丙、丁四名同学表现优秀,现决定从这四名同学中任选两名参加“中学生原创动漫大赛”,请用列表或画树状图的方法求出恰好选中乙、丙两位同学的概率.21. 鄂州市某校数学兴趣小组借助无人机测量一条河流的宽度 .如图所示,一架水平飞行的无人机在A处测得正前方河流的左岸C处的俯角为 ,无人机沿水平线 方向继续飞行50米至B处,测得正前方河流右岸D处的俯角为30°.线段 的长为无人机距地面的铅直高度,点M、C、D在同一条直线上.其中 米. (1)、求无人机的飞行高度 ;(结果保留根号)(2)、求河流的宽度 .(结果精确到1米,参考数据: )22. 如图,四边形ABCD内接于⊙O,对角线AC为⊙O的直径,过点C作AC的垂线交AD的延长线于点E,点F为CE的中点,连接DB, DF.
(1)、求无人机的飞行高度 ;(结果保留根号)(2)、求河流的宽度 .(结果精确到1米,参考数据: )22. 如图,四边形ABCD内接于⊙O,对角线AC为⊙O的直径,过点C作AC的垂线交AD的延长线于点E,点F为CE的中点,连接DB, DF. (1)、求证:DF是⊙O的切线;(2)、若DB平分∠ADC,AB=a,∶DE=4∶1,写出求DE长的思路.23. 某商店购进甲,乙两种商品,已知每件甲种商品的价格比每件乙种商品的价格贵5元,用360元购买甲种商品的件数恰好与用300元购买乙种商品的件数相同.(1)、求甲乙两种商品的价格各是多少元?(2)、某商店计划购买这两种商品共40件,且投入的经费不超过1150元,那么最多可购买多少件甲种商品?(3)、李珍购进了甲,乙这两种商品,共用去145元钱,你知道他甲,乙两种商品各买了多少件吗?24.(1)、【问题情境】
(1)、求证:DF是⊙O的切线;(2)、若DB平分∠ADC,AB=a,∶DE=4∶1,写出求DE长的思路.23. 某商店购进甲,乙两种商品,已知每件甲种商品的价格比每件乙种商品的价格贵5元,用360元购买甲种商品的件数恰好与用300元购买乙种商品的件数相同.(1)、求甲乙两种商品的价格各是多少元?(2)、某商店计划购买这两种商品共40件,且投入的经费不超过1150元,那么最多可购买多少件甲种商品?(3)、李珍购进了甲,乙这两种商品,共用去145元钱,你知道他甲,乙两种商品各买了多少件吗?24.(1)、【问题情境】
如图1,在正方形ABCD中,E,F,G分别是BC,AB,CD上的点,FG⊥AE于点Q.求证:AE=FG.
(2)、【尝试应用】如图2,正方形网格中,点A,B,C,D为格点,AB交CD于点O.求tan∠AOC的值;
(3)、【拓展提升】如图3,点P是线段AB上的动点,分别以AP,BP为边在AB的同侧作正方形APCD与正方形PBEF,连接DE分别交线段BC,PC于点M,N.
①求∠DMC的度数;
②连接AC交DE于点H,直接写出的值.
25. 已知:抛物线与x轴交于A、B两点,点A在点B左侧,将绕点A旋转180゜得到交x轴与点N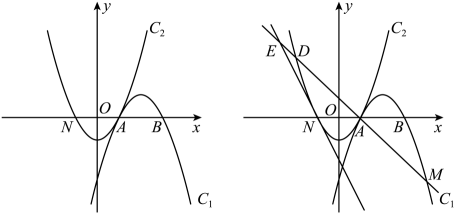 (1)、求的解析式(2)、求证:无论x取何值恒(3)、当时,求m和n的值.(4)、直线经过点N,D是抛物线上第二象限内的一点,设D的横坐标为q,作直线AD交抛物线于点M,交直线于点E,若DM=2ED,求q值
(1)、求的解析式(2)、求证:无论x取何值恒(3)、当时,求m和n的值.(4)、直线经过点N,D是抛物线上第二象限内的一点,设D的横坐标为q,作直线AD交抛物线于点M,交直线于点E,若DM=2ED,求q值