山东省滨州市无棣县2022年九年级数学第一次模拟试题
试卷更新日期:2022-05-26 类型:中考模拟
一、单选题
-
1. 2022年新年贺词中提到“人不负青山,青山定不负人”,下列四个有关环保的图形中,是轴对称图形,但不是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 2021年9月8日,教育部举办新闻发布会,介绍了教师队伍建设进展效,教师总数已经达到1792.97万人,将1792.97万人用科学记数法表示为( )A、0.179297×104万人 B、1.79297×103万人 C、17.9297×102万人 D、1.79297×103人3. 下列运算中,正确的是( )A、 B、 C、 D、4. 如图,在⊙O中,弦 , 圆心O到AB的距离 , 则⊙O的半径长为( )
2. 2021年9月8日,教育部举办新闻发布会,介绍了教师队伍建设进展效,教师总数已经达到1792.97万人,将1792.97万人用科学记数法表示为( )A、0.179297×104万人 B、1.79297×103万人 C、17.9297×102万人 D、1.79297×103人3. 下列运算中,正确的是( )A、 B、 C、 D、4. 如图,在⊙O中,弦 , 圆心O到AB的距离 , 则⊙O的半径长为( )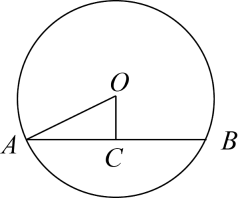 A、2 B、2 C、 D、5. 如图,AB∥CD,∠1=45°,∠3=80°,则∠2的度数为( )
A、2 B、2 C、 D、5. 如图,AB∥CD,∠1=45°,∠3=80°,则∠2的度数为( )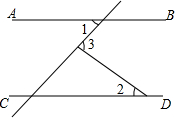 A、30° B、35° C、40° D、45°6. 初三(1)班一次体育模拟考试中,10名同学跳绳项目的测试成绩统计如下表:
A、30° B、35° C、40° D、45°6. 初三(1)班一次体育模拟考试中,10名同学跳绳项目的测试成绩统计如下表:成绩(个/分钟)
140
160
169
170
177
180
人数
1
1
1
2
3
2
则下列说法错误的是( )
A、平均数是170 B、众数是177 C、中位数是173.5 D、方差是1357. 某市从今年1月1日起调整居民用水价格,每立方米水费上涨 .小丽家去年12月份的水费是15元,而今年5月的水费则是30元.已知小丽家今年5月的用水量比去年12月的用水量多5m3.求该市今年居民用水的价格.设去年居民用水价格为x元/m3 , 根据题意列方程,正确的是( )A、 B、 C、 D、8. 不等式组 的解集在数轴上表示正确的是( )A、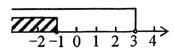 B、
B、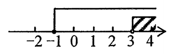 C、
C、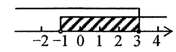 D、
D、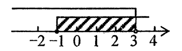 9. 看了《田忌赛马》故事后,小杨用数学模型来分析齐王与田忌的上中下三个等级的三匹马记分如表,每匹马只赛一场,大数为胜,三场两胜则赢,已知齐王的三匹马出场顺序为10,8,6则田忌能赢得比赛的概率为( )
9. 看了《田忌赛马》故事后,小杨用数学模型来分析齐王与田忌的上中下三个等级的三匹马记分如表,每匹马只赛一场,大数为胜,三场两胜则赢,已知齐王的三匹马出场顺序为10,8,6则田忌能赢得比赛的概率为( )马匹
姓名
下等马
中等马
上等马
齐王
6
8
10
田忌
5
7
9
A、 B、 C、 D、10. 如图,四边形OABF中,∠OAB=∠B=90°,点A在x轴上,双曲线过点F,交AB于点E,连接EF.若 , S△BEF=4,则k的值为( )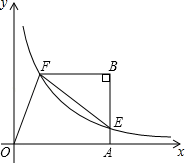 A、6 B、8 C、12 D、1611. 如图,在矩形纸片ABCD中,点E、F分别在矩形的边AB、AD上,将矩形纸片沿CE、CF折叠,点B落在H处,点D落在G处,点C、H、G恰好在同一直线上,若AB=6,AD=4,BE=2,则DF的长是( )
A、6 B、8 C、12 D、1611. 如图,在矩形纸片ABCD中,点E、F分别在矩形的边AB、AD上,将矩形纸片沿CE、CF折叠,点B落在H处,点D落在G处,点C、H、G恰好在同一直线上,若AB=6,AD=4,BE=2,则DF的长是( ) A、2 B、 C、 D、312. 如图,抛物线y=ax2+bx+c(a≠0)与x轴交于点(4,0),其对称轴为直线x=1,结合图象给出下列结论:
A、2 B、 C、 D、312. 如图,抛物线y=ax2+bx+c(a≠0)与x轴交于点(4,0),其对称轴为直线x=1,结合图象给出下列结论:①ac<0;
②4a﹣2b+c>0;
③当x>2时,y随x的增大而增大;
④关于x的一元二次方程ax2+bx+c=0有两个不相等的实数根.
其中正确的结论有( )
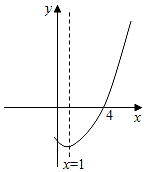 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
13. 若 , 则=.14. 若一元二次方程 无解,则c的取值范围为 .15. 如图,△ABC与△A′B′C′是位似图形,且顶点都在格点上,则位似中心的坐标是 .
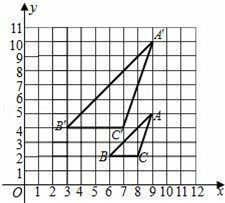 16. 如图,矩形ABCD的对角线AC,BD交于点O,分别以点A,C为圆心,AO长为半径画弧,分别交AB,CD于点E,F.若BD=4,∠CAB=36°,则图中阴影部分的面积为 . (结果保留π).
16. 如图,矩形ABCD的对角线AC,BD交于点O,分别以点A,C为圆心,AO长为半径画弧,分别交AB,CD于点E,F.若BD=4,∠CAB=36°,则图中阴影部分的面积为 . (结果保留π).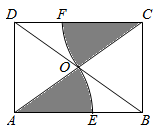 17. 如图所示,顺次连接四边形ABCD各边中点得到四边形EFGH,要使四边形EFGH为矩形,应添加的条件是;要使四边形EFGH为菱形,应添加的条件是(只填序号).备选答案:①AB∥CD;②AC=BD;③AC⊥BD;④AB=DC.
17. 如图所示,顺次连接四边形ABCD各边中点得到四边形EFGH,要使四边形EFGH为矩形,应添加的条件是;要使四边形EFGH为菱形,应添加的条件是(只填序号).备选答案:①AB∥CD;②AC=BD;③AC⊥BD;④AB=DC. 18. 如图在平面直角坐标系中,直线的图像分别与y轴和x轴交于点A,点B.定点P的坐标为 , 点Q是y轴上任意一点,则的最小值为 .
18. 如图在平面直角坐标系中,直线的图像分别与y轴和x轴交于点A,点B.定点P的坐标为 , 点Q是y轴上任意一点,则的最小值为 .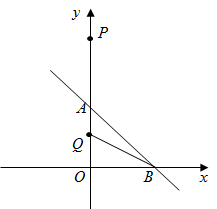
三、解答题
-
19. 先化简,再求值 ,其中 满足方程 。20. 目前,国际上常用身体质量指数“ ”作为衡量人体健康状况的一个指标,其计算公式: ( 表示体重,单位:千克; 表示身高,单位:米).已知某区域成人的 数值标准为: 为瘦弱(不健康): 为偏瘦; 为正常; 为偏胖; 为肥胖(不健康).某研究人员从该区域的一体检中心随机抽取55名成人的体重、身高数据组成一个样本,计算每名成人的 数值后统计如下:
身体属性
人数
瘦弱
2
偏瘦
2
正常
11
偏胖
9
肥胖
(男性身体属性与人数统计表)
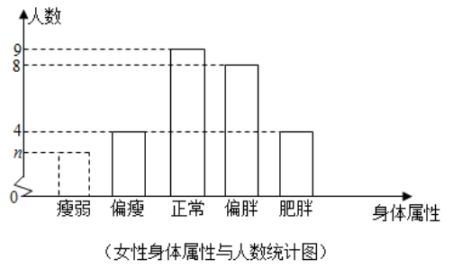 (1)、求这个样本中身体属性为“正常”的人数;(2)、某女性的体重为51.2千克,身高为1.6米,求该女性的 数值;(3)、当 且 ( 、 为正整数)时,求这个样本中身体属性为“不健康”的男性人数与身体属性为“不健康”的女性人数的比值.21. 一列快车和一列慢车同时从甲地出发,分别以速度、(单位: , 且)匀速驶向乙地.快车到达乙地后停留了 , 沿原路仍以速度匀速返回甲地,设慢车行驶的时间为 , 两车之间的距离为 , 图中的折线表示从慢车出发至慢车到达乙地的过程中,与之间的函数关系.
(1)、求这个样本中身体属性为“正常”的人数;(2)、某女性的体重为51.2千克,身高为1.6米,求该女性的 数值;(3)、当 且 ( 、 为正整数)时,求这个样本中身体属性为“不健康”的男性人数与身体属性为“不健康”的女性人数的比值.21. 一列快车和一列慢车同时从甲地出发,分别以速度、(单位: , 且)匀速驶向乙地.快车到达乙地后停留了 , 沿原路仍以速度匀速返回甲地,设慢车行驶的时间为 , 两车之间的距离为 , 图中的折线表示从慢车出发至慢车到达乙地的过程中,与之间的函数关系.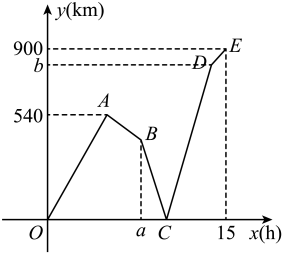 (1)、甲乙两地相距;点实际意义:;(2)、求 , 的值;(3)、慢车出发多长时间后,两车相距?22. 如图,在矩形ABCD中,E是BC边上的点,AE=BC,DF⊥AE,垂足为F,连接DE,
(1)、甲乙两地相距;点实际意义:;(2)、求 , 的值;(3)、慢车出发多长时间后,两车相距?22. 如图,在矩形ABCD中,E是BC边上的点,AE=BC,DF⊥AE,垂足为F,连接DE,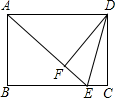 (1)、求证:△ABE≌△DFA.(2)、如果AD=10,AB=6,求sin∠EDF的值.23. 如图,在△ABC中,AB=AC,以AB为直径作圆O,分别交BC于点D,交CA的延长线于点E,过点D作DH⊥AC于点H,连接DE交线段OA于点F.
(1)、求证:△ABE≌△DFA.(2)、如果AD=10,AB=6,求sin∠EDF的值.23. 如图,在△ABC中,AB=AC,以AB为直径作圆O,分别交BC于点D,交CA的延长线于点E,过点D作DH⊥AC于点H,连接DE交线段OA于点F.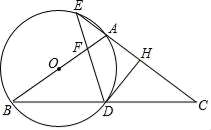 (1)、求证:DH是圆O的切线;(2)、若A为EH的中点,求的值;(3)、若EA=EF=1,求圆O的半径.24. 在平面直角坐标系中,点A、B,C的坐标分别为(0,8),(-2,0),(4,0).
(1)、求证:DH是圆O的切线;(2)、若A为EH的中点,求的值;(3)、若EA=EF=1,求圆O的半径.24. 在平面直角坐标系中,点A、B,C的坐标分别为(0,8),(-2,0),(4,0). (1)、求过A、B、C三点的抛物线的解析式及该抛物线的对称轴和原点坐标;(2)、设点P(m,t)是(1)中所求抛物线对称轴上的一点,求直线BP的解析式及BP与抛物线的另一交点Q的坐标(用含t的式子表示);(3)、当t为何值时?;(4)、在抛物线对称轴上,是否存在这样的点P,使得△ABP为直角三角形?若存在,直接写出点P坐标;若不存在,请说明理由.
(1)、求过A、B、C三点的抛物线的解析式及该抛物线的对称轴和原点坐标;(2)、设点P(m,t)是(1)中所求抛物线对称轴上的一点,求直线BP的解析式及BP与抛物线的另一交点Q的坐标(用含t的式子表示);(3)、当t为何值时?;(4)、在抛物线对称轴上,是否存在这样的点P,使得△ABP为直角三角形?若存在,直接写出点P坐标;若不存在,请说明理由.