(人教版)2021-2022学年度第二学期七年级数学第5.3平行线的性质期末复习测试卷
试卷更新日期:2022-05-26 类型:复习试卷
一、单选题
-
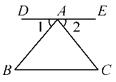
1. 一个三角板和一个直尺拼接成如图所示的图形,其中 ,则 的度数是( ).
 A、10° B、45° C、37.5° D、15°2. 如图, , 的平分线交AE于点B,G是 上的一点, 的平分线交CF于点D,且BC平分 ,下列结论:① ;② ;③与 互余的角有2个;④若 ,则 ,其中正确的是( )
A、10° B、45° C、37.5° D、15°2. 如图, , 的平分线交AE于点B,G是 上的一点, 的平分线交CF于点D,且BC平分 ,下列结论:① ;② ;③与 互余的角有2个;④若 ,则 ,其中正确的是( )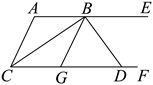 A、①②③④ B、①② C、①②③ D、①②④3. 如图,直线l1∥l2 , 直线l3交l1于点A,交l2于点B,过点A的直线l4⊥l3 , 交l2于点C.若∠1=56°,则∠2的度数为( )
A、①②③④ B、①② C、①②③ D、①②④3. 如图,直线l1∥l2 , 直线l3交l1于点A,交l2于点B,过点A的直线l4⊥l3 , 交l2于点C.若∠1=56°,则∠2的度数为( ) A、 B、 C、 D、4. 如图 ,∠1=∠2=58°,根据尺规作图痕迹,可得∠ADB 的度数是( )
A、 B、 C、 D、4. 如图 ,∠1=∠2=58°,根据尺规作图痕迹,可得∠ADB 的度数是( )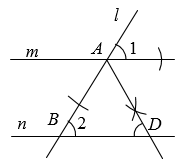 A、58° B、60° C、61° D、122°5. 如图,直线a∥b,射线DC与直线a相交于点C,过点D作DE⊥b于点E,已知∠1=25°,则∠2的度数为( )
A、58° B、60° C、61° D、122°5. 如图,直线a∥b,射线DC与直线a相交于点C,过点D作DE⊥b于点E,已知∠1=25°,则∠2的度数为( )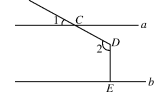 A、105° B、115° C、125° D、165°6. 如图,一条公路经过两次转弯后又回到原来的方向,如果第一次的拐角为 150°,则第二次的拐角为( )
A、105° B、115° C、125° D、165°6. 如图,一条公路经过两次转弯后又回到原来的方向,如果第一次的拐角为 150°,则第二次的拐角为( ) A、40° B、50° C、140° D、150°7. 将一副三角板(含30°、45°、60°)按如图所示的位置摆放在直尺上,则的度数为( )
A、40° B、50° C、140° D、150°7. 将一副三角板(含30°、45°、60°)按如图所示的位置摆放在直尺上,则的度数为( )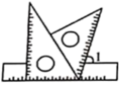 A、75° B、60° C、105° D、95°8. 下列命题正确的是( )A、圆心角的度数等于圆周角的度数的2倍 B、有两边相等的平行四边形是菱形 C、若 , ,且 ,则 有最大值2 D、若 ,则抛物线 与x轴没有交点9. 对于命题“若a2>b2 , 则a>b”,下面四组关于a,b的值中,能说明这个命题是假命题的是( )A、a=3,b=﹣2 B、a=﹣2,b=3 C、a=2,b=﹣3 D、a=﹣3,b=210. 以下四个命题中,真命题的个数为( )
A、75° B、60° C、105° D、95°8. 下列命题正确的是( )A、圆心角的度数等于圆周角的度数的2倍 B、有两边相等的平行四边形是菱形 C、若 , ,且 ,则 有最大值2 D、若 ,则抛物线 与x轴没有交点9. 对于命题“若a2>b2 , 则a>b”,下面四组关于a,b的值中,能说明这个命题是假命题的是( )A、a=3,b=﹣2 B、a=﹣2,b=3 C、a=2,b=﹣3 D、a=﹣3,b=210. 以下四个命题中,真命题的个数为( )
(1)已知等腰△ABC中,AB=AC,顶角∠A=36°,一腰AB的垂直平分线交AC于点E,AB 为点D,连接BE,则∠EBC的度数为36°;(2)经过一点有且只有一条直线与这条直线平行;(3)长度相等的弧是等弧;(4)顺次连接菱形各边得到的四边形是矩形.A、1个 B、2个 C、3个 D、4个二、填空题
-
11. 平分 , DE∥AC .若 ,则 = °.
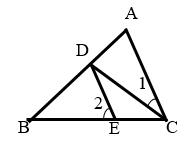 12. 一副直角三角板如图放置,点A在DE上,若BC∥DE,则 的度数为.
12. 一副直角三角板如图放置,点A在DE上,若BC∥DE,则 的度数为. 13. 如图,AB∥CD,∠ABE=148°,FE⊥CD于E,则∠FEB的度数是度.
13. 如图,AB∥CD,∠ABE=148°,FE⊥CD于E,则∠FEB的度数是度.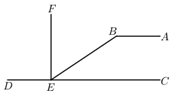 14. “对顶角相等”是命题.(填“真”或“假”)15. 把命题“平行于同一条直线的两条直线互相平行”改写成“如果……,那么……”形为
14. “对顶角相等”是命题.(填“真”或“假”)15. 把命题“平行于同一条直线的两条直线互相平行”改写成“如果……,那么……”形为三、解答题
-
16. 在下列解题过程的空白处填上适当的内容(推理的理由或数据).
如图, , , ,那么 吗?说明理由.
解: ,理由如下:
因为 , (已知)
所以
所以 ( ).
所以 ( ).
所以 ( ).
( ).
因为 ,
所以 .
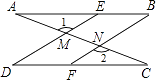
 17. 如图,已知直线AB∥CD,直线MN分别交AB、CD于M、N两点,若ME、NF分别是∠AMN、∠DNM的角平分线,试说明:ME∥NF
17. 如图,已知直线AB∥CD,直线MN分别交AB、CD于M、N两点,若ME、NF分别是∠AMN、∠DNM的角平分线,试说明:ME∥NF 18. 如图,AB⊥CD,AB⊥EF.求证:∠1=∠3.
18. 如图,AB⊥CD,AB⊥EF.求证:∠1=∠3. 19. 如图,已知 , 求证: .
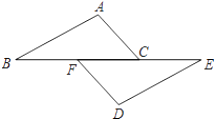
19. 如图,已知 , 求证: . 20. 已知:如图,B、D分别在AC、CE上,AD是∠CAE的平分线,BD∥AE,AB=BC.
20. 已知:如图,B、D分别在AC、CE上,AD是∠CAE的平分线,BD∥AE,AB=BC.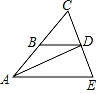
求证:AC=AE.