山东省淄博市高青县2021-2022学年八年级下学期期中数学试题

试卷更新日期：2022-05-26 类型：期中考试

进入出卷网下载

一、单选题

1. 二次根式 $\frac{1}{\sqrt{x - 2}}$ 有意义，则x满足的条件是（）

A、 $x < 2$ B、 $x > 2$ C、 $x \geq 2$ D、 $x \leq 2$

查看试题解析
2. 若一元二次方程 $(k - 1) x^{2} + 3 x + k^{2} - 1 = 0$ 有一个解为 $x = 0$ ，则k为（）

A、 $± 1$ B、1 C、 $- 1$ D、0

查看试题解析
3. 菱形ABCD的周长是8cm，∠ABC＝60°，那么这个菱形的对角线BD的长是（　　）

A、 $\sqrt{3}$ cm B、2 $\sqrt{3}$ cm C、1cm D、2cm

查看试题解析
4. 下列各组二次根式，不是同类二次根式的一组是（）

A、 $\sqrt{8}$ 与 $\sqrt{32}$ B、 $\sqrt{45}$ 与 $\sqrt{20}$ C、 $\sqrt{27}$ 与 $\sqrt{75}$ D、 $\sqrt{24}$ 与 $\sqrt{80}$

查看试题解析
5. 如图，O是矩形ABCD的对角线AC的中点，M是AD的中点．若AB＝5，AD＝12，则四边形ABOM的周长为（）

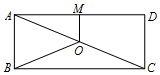A、16 B、20 C、29 D、34

查看试题解析
6. 若 $x_{1}$ ， $x_{2}$ 是 $x^{2} + b x - 3 b = 0$ 的两个根，且 $x_{1}^{2} + x_{2}^{2} = 7$ ，则b的值是（）

A、1 B、 $- 7$ C、1或7 D、7或 $- 1$

查看试题解析
7. 如图，在一个长方形中无重叠的放入面积分别为 $16 c m^{2}$ 和 $12 c m^{2}$ 的两张正方形纸片，则图中空白部分的面积为（）

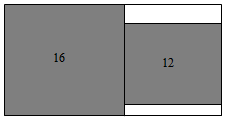A、 $(4 - 2 \sqrt{3}) c m^{2}$ B、 $(8 \sqrt{3} - 4) c m^{2}$ C、 $(8 \sqrt{3} - 12) c m^{2}$ D、 $8 c m^{2}$

查看试题解析
8. 已知方程 $x^{2} - 6 x + 4 = □$ ，等号右侧的数字印刷不清楚，若可以将其配方成 ${(x - p)}^{2} = 7$ 的形式，则印刷不清楚的数字是（）

A、6 B、9 C、2 D、 $- 2$

查看试题解析
9. 化简二次根式 $\frac{1}{x} \sqrt{- x^{3}}$ 的正确结果是（）

A、 $\sqrt{- x}$ B、 $\sqrt{x}$ C、 $- \sqrt{x}$ D、 $- \sqrt{- x}$

查看试题解析
10. 已知 $α ， β$ 是方程 $x^{2} + 2017 x + 1 = 0$ 的两个根，则 $(1 + 2020 α + α^{2}) (1 + 2020 β + β^{2})$ 的值为（）

A、9 B、10 C、12 D、15

查看试题解析
11. 如图，在边长为4正方形 $A B C D$ 的外部作 $R t △ A E F$ ， $A E = A F = 2$ ，连接 $D E ， B F ， B D$ ，则 $D E^{2} + B F^{2} =$ （）

A、10 B、20 C、30 D、40

查看试题解析
12. 对于一元二次方程 $a x^{2} + b x + c = 0 (a \neq 0)$ ，下列说法：
①若 $a + b + c = 0$ ，则 $b^{2} - 4 a c \geq 0$ ；
②若方程 $a x^{2} + c = 0$ 有两个不相等的实根，则方程 $a x^{2} + b x + c = 0$ 必有两个不相等的实根；
③若c是方程 $a x^{2} + b x + c = 0$ 的一个根，则一定有 $a c + b + 1 = 0$ 成立；
②若 $x_{0}$ 是一元二次方程 $a x^{2} + b x + c = 0$ 的根，则 $b^{2} - 4 a c = {(2 a x_{0} + b)}^{2}$ 其中正确的（）

A、只有①②④ B、只有①②③ C、①②③④ D、只有①②

查看试题解析

二、填空题

13. 计算 $\sqrt{12} \div \sqrt{2}$ 的结果是．

查看试题解析
14. 若1和2是方程 $x^{2} + m x + n = 0$ 的两根，则 $m \cdot n =$

查看试题解析
15. 如图，点E，F在正方形ABCD的对角线AC上，AC＝10，AE＝CF＝3，则四边形BFDE的面积为．

查看试题解析
16. 若a、b是方程 $x^{2} + x - 2022 = 0$ 的两根，则 $a^{2} + 2 a + b =$ ．

查看试题解析
17. 如图，在矩形ABMN中，AN＝ $\sqrt{2}$ ，点C是MN的中点，分别连接AC，BC，且BC＝2 $\sqrt{2}$ ，点D为AC的中点，点E为边AB上一个动点，连接DE，点A关于直线DE的对称点为点F，分别连接DF，EF，当EF⊥AC时，AE的长为．

查看试题解析

三、解答题

18. 计算：

(1)、 $2 \sqrt{18} - \sqrt{32} + \sqrt{2}$

(2)、 $(\sqrt{12} - \sqrt{24}) \div \sqrt{6} - 2 \sqrt{\frac{1}{2}}$

查看试题解析
19. 解方程：

(1)、 $3 x^{2} - 4 x - 2 = 0$

(2)、 $5 x (x - 2) = 2 (x - 2)$

查看试题解析
20. 如图所示，菱形ABCD的对角线AC与BD交于点O，分别过点C、点D作BD、AC的平行线交于点E，连接EO交CD于点F．

(1)、求证：四边形DECO是矩形；

(2)、若 $A D = 3$ ，求OE的长．

查看试题解析
21. 已知关于x的一元二次方程x²﹣mx﹣2＝0…①

(1)、若x＝﹣1是方程①的一个根，求m的值和方程①的另一根；

(2)、对于任意实数m ，判断方程①的根的情况，并说明理由．

查看试题解析
22. 如图，在平行四边形 $A B C D$ 中，P是对角线 $B D$ 上的一点，过点C作 $C Q / / D B$ ，且 $C Q = D P$ ，连接 $A P$ ， $B Q$ ， $P Q$ .

(1)、求证： $A P = B Q$ ；

(2)、若 $∠ A B P + ∠ B Q C = 180 °$ ，求证：四边形 $A B Q P$ 为菱形.

查看试题解析
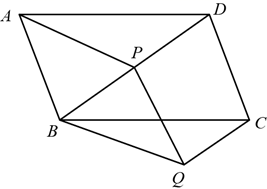23. 小明在解决问题：已知a＝ $\frac{1}{2 + \sqrt{3}}$ ，求2a²－8a＋1的值，他是这样分析与解答的：
因为a＝ $\frac{1}{2 + \sqrt{3}}$ ＝ $\frac{2 - \sqrt{3}}{(2 + \sqrt{3}) (2 - \sqrt{3})}$ ＝2－ $\sqrt{3}$ ，

所以a－2＝－ $\sqrt{3}$ .

所以(a－2)²＝3，即a²－4a＋4＝3.

所以a²－4a＝－1.

所以2a²－8a＋1＝2(a²－4a)＋1＝2×(－1)＋1＝－1.

请你根据小明的分析过程，解决如下问题：

(1)、计算： $\frac{1}{\sqrt{2} + 1}$ = － .

(2)、计算： $\frac{1}{\sqrt{2} + 1} + \frac{1}{\sqrt{3} + \sqrt{2}} + \frac{1}{\sqrt{4} + \sqrt{3}}$ ＋…＋ $\frac{1}{\sqrt{100} + \sqrt{99}}$ ；

(3)、若a＝ $\frac{1}{\sqrt{2} - 1}$ ，求4a²－8a＋1的值.

查看试题解析
24. 已知正方形 $A B C D$ ，点F是射线 $D C$ 上一动点（不与C，D重合），连接 $A F$ 并延长交直线 $B C$ 于点E，交 $B D$ 于点H，连接 $C H$ ，过点C作 $C G ⊥ H C$ 交 $A E$ 于点G．

(1)、若点F在边 $C D$ 上，如图1．
①证明： $∠ D A H = ∠ D C H$
②猜想线段 $C G$ 与 $E F$ 的数量关系并说明理由

(2)、取 $D F$ 中点M，连结 $M G$ ，若 $M G = 4$ ，正方形边长为6，求 $B E$ 的长

查看试题解析