山东省青岛市胶州市2021-2022学年八年级下学期期中数学试题

试卷更新日期：2022-05-26 类型：期中考试

进入出卷网下载

一、单选题

1. 图书馆的标志是浓缩图书馆文化的符号，下列图书馆标志中，是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 某电梯标明“最大载重量：1000 kg”，若电梯载重量为x，x为非负数，则“最大载重量1000kg”用不等式表示为（）

A、 $x > 1000$ B、 $x < 1000$ C、 $x \geq 1000$ D、 $x \leq 1000$

查看试题解析
3. 下列命题的逆命题是真命题的是（）

A、对顶角相等 B、全等三角形对应角相等 C、互为相反数的两个数绝对值相等 D、直角三角形的两个锐角互余

查看试题解析
4. 某公园的A，B，C处分别有海资船、摩天轮、旋转木马三个娱乐项目，现要在公园内一个售票中心，使三个娱乐项目所处位置到售票中心的距离相等，则售票中心应建立在（）

A、△ABC三边高线的交点处 B、△ABC三角角平分线的交点处 C、△ABC三边中线的交点处 D、△ABC三边垂直平分线的交点处

查看试题解析
5. 如图，在Rt△ABC中， $∠ B = 90 °$ ， $∠ A C B = 30 °$ ， $A B = 2$ ．将△ABC沿BC方向向右平移得到△DEF，若四边形ACFD的周长为10，则△ABC平移的距离为（）

A、1 B、2 C、 $2 \sqrt{3}$ D、4

查看试题解析
6. 如图，在平面直角坐标系中，点A的坐标为 $(- 2 ， 3)$ ，将点A烧原点O逆时针方向旋转 $90 °$ 得到点B，则点B的坐标为（）

A、 $(- 2 ， - 3)$ B、 $(- 3 ， - 2)$ C、 $(2 ， 3)$ D、 $(3 ， 2)$

查看试题解析
7. 如图，在△ABC中， $∠ A C B = 90 °$ ， $A C = B C$ ， D为BC延长线上一点，点E在AC上， $A D = B E$ ．若 $∠ A B E = 35 °$ ，则∠BAD的度数为（）

A、 $35 °$ B、 $45 °$ C、 $55 °$ D、 $65 °$

查看试题解析
8. 若不等式组 ${\begin{array}{l} x + m > 2 \\ n - x > - 4 \end{array}$ 的解集为 $1 < x < 2$ ，则 ${(m + n)}^{2022}$ 的值为（）

A、 $- 1$ B、0 C、1 D、2

查看试题解析

二、填空题

9. 若m＜n，则 $- 3 m + 2$ $- 3 n + 2$ （用“＞”，“＝”或“＜”填空）

查看试题解析
10. △ABC的三个顶点坐标分别是 $A (a ， 5)$ ， $B (7 ， b)$ ， $C (4 ， 9)$ ，将△ABC平移后得到 $△ A_{1} B_{1} C_{1}$ ，其中 $A_{1} (3 ， 8)$ ， $B_{1} (6 ， 3)$ ，则点 $C_{1}$ 的坐标是．

查看试题解析
11. 如图，CD是等边△ABC的中线， $D E ⊥ A C$ ，垂足为点E．若DE的长度为3cm，则点D到BC的距离为cm．

查看试题解析
12. 一次函数 $y = k x + b$ 的图象如图所示，当 $0 < k x + b < 3$ 时，x的取值范围为．

查看试题解析
13. 如图，点O为等边△ABC内一点 $A O = 8$ ， $B O = 6$ ， $C O = 10$ ，将△AOC绕点A顺时针方向旋转 $60 °$ ，使AC与AB重合，点O旋转至点 $O_{1}$ 处，连接 $O O_{1}$ ，则 $△ B O O_{1}$ 的面积是．

查看试题解析
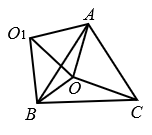14. 如图，在△ABC中，AB=AC=10，BC=12，点D是边BC的中点，直线MN是AB的垂直平分线，点E是MN上的一个动点，则△BDE周长的最小值是．

查看试题解析
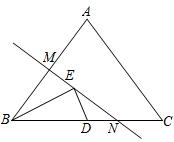15. 如图，直线a，b交于点O，∠α=40°，点A是直线a上的一个定点，点B在直线b上运动，且始终位于直线a的上方，若以点O，A，B为顶点的三角形是等腰三角形，则∠OAB=°．

查看试题解析
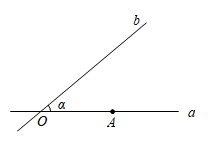16. 如图，在平面直角坐标系中，点A，B，C的坐标分别为 $(1 ， 1)$ ， $(3 ， 0)$ ， $(2 ， - 1)$ ．点M从坐标原点O出发，第一次跳跃到点 $M_{1}$ ，使得点 $M_{1}$ 与点O关于点A成中心对称；第二次跳跃到点 $M_{2}$ ，使得点 $M_{2}$ 与点 $M_{1}$ 关于点B成中心对称；第三次跳跃到点 $M_{3}$ ，使得点 $M_{3}$ 与点 $M_{2}$ 关于点C成中心对称；第四次跳跃到点 $M_{4}$ ，使得点 $M_{4}$ 与点 $M_{3}$ 关于点A成中心对称；…，依此方式跳跃，点 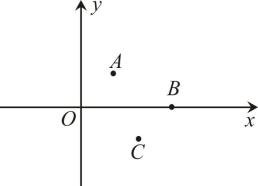$M_{2022}$ 的坐标是．

查看试题解析

三、解答题

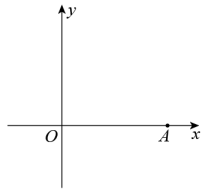
17. 已知：如图，点A是平面直角坐标系x轴上的一点．
求作：点P，使点P在第一象限内，点P到两坐标轴的距离相等，且与点A的距离最近．

查看试题解析
18.

(1)、解不等式： $3 x - 8 > 2 (x - 1)$ ；

(2)、解不等式： $\frac{x - 1}{4} - \frac{1}{2} \leq x$ ，并把它的解集表示在数轴上；

(3)、解不等式组： ${\begin{array}{l} 3 x - 4 < 2 (x + 1) \\ \frac{4 x + 1}{3} - \frac{3 x + 1}{2} \leq 1 \end{array}$ ；

(4)、解不等式组； $\frac{2}{5} < 1 - \frac{x}{5} < \frac{3}{2}$ ，并写出满足此不等式组的所有整数解．

查看试题解析
19. 在Rt△ABC中， $∠ B A C = 90 °$ ， AE是斜边BC上的高，角平分线BD交AE于点G，交AC于点D， $D F ⊥ B C$ 于点F．

(1)、求证： $A B = B F$ ；

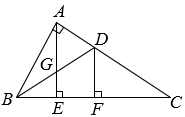(2)、试判断AD与AG有怎样的数量关系？请说明理由．

查看试题解析
20. 每年6月5日是“世界环境日”，某小区为积极响应“共建清洁美丽世界”的号召，计划购进A，B两种树苗共60棵美化小区环境，已知A种树苗每棵130元，B种树苗每棵150元，若购进A种树苗的数量不多于B种树苗的两倍，则A，B两种树苗各购进多少棵时，费用最省？最省费用是多少？

查看试题解析
21. 如图，在Rt△ABC中，∠BAC=90°，AB=AC，D是BC边上的一点，连接AD，将线段AD绕点A按顺时针方向旋转90°得到线段AE，分别连接BE，DE．

(1)、求证：△AEB≌△ADC；

(2)、当BC=4，BD=3时，求ED的长．

查看试题解析
22. 某主题乐园推出了甲、乙两种方式的门票优惠活动，图中 $l_{1}$ ， $l_{2}$ 分别表示甲、乙两种方式所需费用y（元）与入园次数x（次）之间的函数关系，请解答下列问题：

(1)、分别求出选择这两种优惠方式时，y与x之间的函数关系式；

(2)、什么情况下，选择甲种优惠方式更合算？

查看试题解析
23. 问题提出：
如图a所示的5×3网格（每一个小正方形的边长均为单位长度1）中，共有多少个长方形（包含正方形）？

问题探究：

为了解决上面的问题，我们先从最简单的情形入手，从中找到解决问题的方法，最后出一般性的结论，为了更好的探究规律，在本次探究过程中，我们约定所有长方形横向为长，竖向为宽．

探究一：

对于1×1同格（如图①），显然，只有1个长方形．

对于1×2同格（如图②），所有长方形的宽均为1，长可能是1，也可能是2．按照从小到大的顺序，长为1的长方形有2个，长为2的长方形有1个，所以共有 $2 + 1 = 3$ 个长方形．

而2对于1×3网格（如图③），所有长方形的宽均为1，长可能是1，可能是2，可能是3，按照从小到大的顺序，长为1的长方形有3个，长为2的长方形有2个，长为3的长方形有个，所以，共 $3 + 2 + 1 = 6$ 个长方形．

探究二：

对于2×1网格（如图④），所有长方形的长均为1，宽可能是1，可能是2．宽为1时可以看成由2个1×1网格组成，长方形有2×1个；宽为2时，把中间的横线隐去，就可以看成由1个“图①”组成，所以长方形有1×1个，因此，共有 $(2 + 1) \times 1$ 个长方形．

对于2×2网格（如图⑤），长方形的宽可能是1，可能是2．宽为1时，可以看成由2个1×2回格组成，所以长方形有 $2 \times (2 + 1)$ 个；宽为2时，把中间的横线隐去，就可以看成中1个“图②”组成，所以长方形有 $(2 + 1)$ 个，因此，共在 $(2 + 1) \times (2 + 1)$ 个长方形．

对于2×3网格（如图⑥），长方形的宽可能是1，可能是2．宽为1时，可以看成由2个1×3网格组成，长方形 $2 \times (3 + 2 + 1)$ 个；宽为2时，可把中间的横线隐去，就可以看成由1个“图③”网格组成，所以长方形有 $(3 + 2 + 1)$ 个，因此，共有 $(2 + 1) \times (3 + 2 + 1)$ ）个长方形．

探究三：

对于3×1网格（如图⑦），长方形的长均为1，宽可能是1，可能是2，可能是3．宽为1时，可以看成由3个1×1网格组成，所以长方形3×1个；宽为2时，把中间的横线是隐去，就可以看成由2个“图①”网格组成，所以长方形2×1个；宽为3时，把中间的横线隐去，就可以看成由1个“图①”网格组成，所以长方形有1×1个．因此，共有 $(3 + 2 + 1) \times 1$ 个长方形．

对于3×2网格（如图⑧），长方形的宽可能是1，可能是2，可能是3．宽为1时，可以看成由3个1×2网格组成，所以长方形有 $3 \times (2 + 1)$ 个；宽为2时，把中间的横线隐去，就可以看成由2个“图②”同格组成，所以长方形有 $2 \times (2 + 1)$ 个；宽为3时，把中间的横线隐去，就可以看成由1个“图②”同格组成，所以长方形有 $1 \times (2 + 1)$ 个，因此，共有 $(3 + 2 + 1) \times (2 + 1)$ 个长方形．

对于3×3网格（如图⑨），长方形的宽可能是1，可能是2，可能是3．宽为1时，可以看成由3个1×3网格组成，所以长方形有 $3 \times (3 + 2 + 1)$ 个；宽为2时，把中间的横线除去就可以看成由2个“图③”网格组成，所以长方形在 $2 \times (3 + 2 + 1)$ 个；宽为3时，把中间的横线隐去，就可以看成由1个“图③”网格组成，所以长方形有 $1 \times (3 + 2 + 1)$ 个，因此，共有 $(3 + 2 + 1) \times (3 + 2 + 1)$ 个长方形．

(1)、探究四：

4×1同格中共有个长方形；4×2网格中共有个长方形；4×3网格中共有个长方形．

(2)、问题解决：
5×3网格中共有个长方形．

(3)、拓展延伸：
①5×4同格中共有个长方形．

②6×7网格中共有个长方形．

③m×n网格中共有个长方形．

(4)、类比应用：
如图所示的网格中有个平行四边形．

查看试题解析
24. 如图，在等边△ABC中，AB=AC=BC=6cm，点P从点B出发，沿BA方向匀速运动，速度为1cm/s；点Q从点C出发，沿CB方向匀速运动，速度为2cm/s，分别连接PQ，AQ．设运动时间为t（s）（0<t<3），解答下列问题：

(1)、当AQ平分∠BAC时，求t的值；

(2)、当t为何值时，点P在线段BQ的垂直平分线上；

(3)、设四边形APQC的面积为S（cm²），求S与t之间的函数关系式；

(4)、在运动过程中，是否存在某一时刻t，使△BPQ为直角三角形？若存在，求出t的值；若不存在，请说明理由．

查看试题解析