江西省萍乡市湘东区2021-2022学年七年级下学期期中数学试题

试卷更新日期：2022-05-26 类型：期中考试

进入出卷网下载

一、单选题

1. 下列计算中正确的是（）

A、 $a^{4} + a^{5} = a^{9}$ B、 $a^{3} \cdot a^{3} \cdot a^{3} = 3 a^{3}$ C、 $2 a^{4} \cdot 3 a^{5} = 6 a^{9}$ D、 ${(- a^{3})}^{4} = a^{7}$

查看试题解析
2. 已知三角形的两边长分别为4cm和9cm，则下列长度的线段能作为第三边的是（）

A、13cm B、6cm C、5cm D、4m

查看试题解析
3. 如果 $(x - 5) (2 x + m)$ 的积中不含x的一次项，则m的值是（）

A、5 B、10 C、 $- 5$ D、 $- 10$

查看试题解析
4. 三角形的角平分线、中线、高线（）

A、每一条都是线段 B、角平分线是射线，其余是线段 C、高线是直线，其余为线段 D、高线是直线，角平分线是射线，中线是线段

查看试题解析
5. 要使 $4 x^{2} + 25 + m x$ 成为一个完全平方式，则 $m$ 的值是（）

A、 $10$ B、 $\pm 10$ C、20 D、 $\pm 20$

查看试题解析
6. 一个学员在广场上驾驶汽车，两次拐弯后，行驶的方向与原来的方向相同，这两次拐弯的角度可能是（）

A、第一次向右拐 50° ，第二次向左拐130 B、第一次向右拐 50° ，第二次向右拐130° C、第一次向左拐 50° ，第二次向左拐130 D、第一次向左拐 30° ，第二次向右拐 30°

查看试题解析
7. 弹簧挂上物体后会伸长，测得一弹簧的长度y（厘米）与所挂物体的质量x（千克）间有下面关系（假设弹簧不会折断）：
x
0
1
2
3
4
5
y
10
10.5
11
11.5
12
12.5
下列说法错误的是（）

A、x与y都是变量，且x自变量，y是因变量 B、弹簧不挂重物时的长度为10厘米 C、物体质量每增加1千克，弹簧长度y增加0.5厘米 D、所挂物体质量为26千克时，弹簧长度为23.5厘米

查看试题解析
8. 如图，OA⊥OB，OC⊥OD，O是垂足，∠AOD＝120°，那么∠COB的度数为（）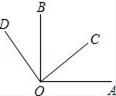

A、80° B、70° C、60° D、50°

查看试题解析
9. 设（5a+3b）²=（5a-3b）²+A，则A等于（）

A、60ab B、30ab C、15ab D、12ab

查看试题解析
10. 如图，AB∥EF，∠C=90°，则a、B、y的关系是（）

A、β+γ-α=90° B、α+β-γ=90° C、α+β+γ=180° D、β=α+γ

查看试题解析

二、填空题

11. 某种生物孢子的直径为0.00063m，用科学记数法表示为m．

查看试题解析
12. 三角形的底边是12厘米，当底边上的高h（厘米）变化时，三角形的面积S（平方厘米）也随着高的变化而变化，可用式子表示成 $S =$ ．

查看试题解析
13. 已知a+b＝3，a²+b²＝5，则ab的值是．

查看试题解析
14. 如图，直线AB∥CD，直线EF分别交AB、CD于点E、F，EG平分∠BEF交CD于G．若∠1=50°，则∠2= ．

查看试题解析
15. 已知 $x^{a} = 3$ ， $x^{b} = 5$ ，则 $x^{3 a - 2 b} =$ ．

查看试题解析
16. 假定甲、乙两人在一次赛跑中，路程与时间的关系如图所示，那么可以知道：（1）甲、乙两人中先到达终点的是；（2）乙在这次赛跑中的速度为m/s.

查看试题解析
17. 计算 $(a - b) (a + b) (a^{2} + b^{2}) (a^{4} - b^{4})$ 的结果是．

查看试题解析
18. 在 $△ A B C$ 中， $∠ A - ∠ B = 15 °$ ， $∠ C = 75 °$ ，则 $∠ A =$ ．

查看试题解析

三、解答题

19. 计算：

(1)、 $5^{2} - {(\frac{1}{3})}^{- 2} + (- 7)^{0}$

(2)、 ${(2 x^{2} y)}^{3} \cdot (- 7 x y^{2}) \div (14 x^{4} y^{3})$

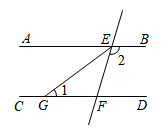
查看试题解析
20. 已知一个角的余角等于它的补角的 $\frac{1}{3}$ ，求这个角的度数．

查看试题解析
21. 先化简再求值： $(3 a - b)^{2} - 3 (2 a + b) (2 a - b) + 3 a^{2}$ ，其中 $a = - 1$ ， $b = 2$ ．

查看试题解析
22. 如图， $A B$ $∥$ $C D$ ，直线 $E F$ 分别交 $A B$ 、 $C D$ 于点 $E$ 、 $F$ ， $E G$ 平分 $∠ A E F$ ，交 $C D$ 于 $G$ ．已知∠1=40°，求∠2的度数．

查看试题解析
23. 如图所示，图象反映的是：张阳从家里跑步去体育场，在那里锻炼了一阵后又走到文具店去买笔，然后走回家，其中x表示时间，y表示张阳离家的距离．根据图象回答下列问题：

(1)、体育场离张阳家千米；

(2)、体育场离文具店千米；张阳在文具店逗留了分钟；

(3)、请计算：张阳从文具店到家的平均速度约是每小时多少千米？

查看试题解析
24. 如图所示， $∠ B A P$ 与 $∠ A P D$ 互补， $∠ B A E = ∠ C P F$ .求证： $∠ E = ∠ F$ .

查看试题解析
25. 乘法公式的探究及应用．

(1)、如图，若将阴影部分裁剪下来，重新拼成一个长方形，面积是（写成多项式乘法的形式）

(2)、比较左、右两图的阴影部分面积，可以得到乘法公式（用式子表达）．

(3)、运用你所得到的公式，计算下列各题：
① $10.3 \times 9.7$
② $(2 m + n - p) (2 m - n + p)$

查看试题解析
26. 如图，已知 $l_{1} ∥ l_{2}$ ，射线 $M N$ 分别和直线 $l_{1} ， l_{2}$ 交于点 $A ， B$ ，射线 $M E$ 分别和直线 $l_{1} ， l_{2}$ 交于点 $C ， D$ ，点 $P$ 在射线 $M N$ 上运动（ $P$ 点与 $A ， B ， M$ 三点不重合），设 $∠ P D B = α$ ， $∠ P C A = β$ ， $∠ C P D = γ$ ．

(1)、如果点 $P$ 在 $A ， B$ 两点之间运动时， $α ， β ， γ$ 之间有何数量关系？请说明理由；

(2)、如果点 $P$ 在 $A ， B$ 两点之外运动时， $α ， β ， γ$ 之间有何数量关系？（只需写出结论，不必说明理由）

查看试题解析

x	0	1	2	3	4	5
y	10	10.5	11	11.5	12	12.5