北京市房山区2021-2022学年八年级下学期期中数学试题
试卷更新日期:2022-05-26 类型:期中考试
一、单选题
-
1. 在平面直角坐标系中,如果点A的坐标为 ,那么点A一定在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限2. 下列曲线中,不是的函数的是( )A、
 B、
B、 C、
C、 D、
D、 3. 下面的多边形中,内角和与外角和相等的是( )A、
3. 下面的多边形中,内角和与外角和相等的是( )A、 B、
B、 C、
C、 D、
D、 4. 在四边形 中, ,如果再添加一个条件,即可推出该四边形是正方形,这个条件可以是( )A、 B、 C、 D、5. 如图,平面直角坐标系中有、、、四个点,一次 函数的图象经过点和另外三个点中的一个,判断下列哪一个点一定不在一次函数的图象上( )
4. 在四边形 中, ,如果再添加一个条件,即可推出该四边形是正方形,这个条件可以是( )A、 B、 C、 D、5. 如图,平面直角坐标系中有、、、四个点,一次 函数的图象经过点和另外三个点中的一个,判断下列哪一个点一定不在一次函数的图象上( ) A、点 B、点 C、点 D、不确定6. 如图,矩形的对角线、相交于点 , , , 则的长为( )
A、点 B、点 C、点 D、不确定6. 如图,矩形的对角线、相交于点 , , , 则的长为( ) A、6 B、 C、 D、7. 如图,已知正比例函数与一次函数的图象交于点 . 下面结论正确的是( )
A、6 B、 C、 D、7. 如图,已知正比例函数与一次函数的图象交于点 . 下面结论正确的是( ) A、; B、当时,; C、当时,; D、当时, .8. 小苏和小林在一条 300 米的直道上进行慢跑,先到终点的同学会在跑道的尽头等待.在整个过程中,小苏和小林之间的距离(单位:米) 与跑步时间(单位:秒) 的对 应关系如下图所示.下列命题中正确的是( )
A、; B、当时,; C、当时,; D、当时, .8. 小苏和小林在一条 300 米的直道上进行慢跑,先到终点的同学会在跑道的尽头等待.在整个过程中,小苏和小林之间的距离(单位:米) 与跑步时间(单位:秒) 的对 应关系如下图所示.下列命题中正确的是( )
①小苏和小林在第19秒时相遇;②小苏和小林之间的最大距离为30米;
③先到终点的同学用时58秒跑完了全程;④先到终点的同学用时50秒跑完了全程;
A、①② B、①②③ C、①②④ D、②③二、填空题
-
9. 函数 中,自变量x的取值范围是 .10. 已知点和点在一次函数的图象上,则 . (填“ > ”,“= ”或“<”)11. 已知一个多边形的内角和为540°,则这个多边形是边形.12. 在ABCD中,∠A:∠B=2:3,则∠C的度数为°.13. 在平面直角坐标系中,的顶点、、的坐标分别是 , , , 则顶点的坐标是 .14. 如图 1 ,菱形纸片的面积为 , 对角线的长为 , 将这个菱形纸片沿对角线剪开,得到四个全等的直角三角形,将这四个直角三角形按图2 所示的方法拼成正方形.则大正方形中空白小正方形的边长是 .
 15. 若直线与两坐标轴围成的三角形的面积为6,则这条直线与轴的交点坐标为 .16. 在四边形中,对角线 , 交于点 . 现存在以下四个条件:①;②;③;④平分 . 从中选取三个条件,可以判定四边形为菱形. 则可以选择的条件序号是(写出所有可能的情况).
15. 若直线与两坐标轴围成的三角形的面积为6,则这条直线与轴的交点坐标为 .16. 在四边形中,对角线 , 交于点 . 现存在以下四个条件:①;②;③;④平分 . 从中选取三个条件,可以判定四边形为菱形. 则可以选择的条件序号是(写出所有可能的情况).三、解答题
-
17. 在平面直角坐标系 中,已知一次函数 的图像与 轴交于点 ,与 轴交于点
 (1)、求 两点的坐标(2)、在给定的平面直角坐标系中画出该函数的图象;(3)、根据图像回答:当 时, 的取值范围是.18. 如图,浩宇的家、食堂、图书馆在同一条直线上.浩宇从家去食堂吃早餐,吃完早餐发现忘带借书卡了,回家途中遇到妈妈给他送来了借书卡,便高兴地去图书馆读书,然后回家.下图反映了这个过程中浩宇离家的距离与时间之间的对应关系.
(1)、求 两点的坐标(2)、在给定的平面直角坐标系中画出该函数的图象;(3)、根据图像回答:当 时, 的取值范围是.18. 如图,浩宇的家、食堂、图书馆在同一条直线上.浩宇从家去食堂吃早餐,吃完早餐发现忘带借书卡了,回家途中遇到妈妈给他送来了借书卡,便高兴地去图书馆读书,然后回家.下图反映了这个过程中浩宇离家的距离与时间之间的对应关系.
根据图象回答下列问题:
(1)、浩宇吃早餐用了分钟,浩宇与妈妈相遇时他离图书馆千米,浩宇从图书馆回家的平均速度是每分钟千米;(2)、浩宇到达食堂之前离家的距离与时间之间的函数关系式为;(3)、你还能从图中发现什么信息 (写出一条即可) .19. 尺规作图:作一条线段的中点.已知:线段 , 如图 1 所示.
求作:点 , 使点是线段 的中点.
作法:①如图 2 ,在上方选取一点 , 连接 , ;
②以点为圆心 ,线段的长为半径作弧;再以点为 圆心,线段的 长为半径作弧,两弧在下方交于点;
③连结 , 与线段交于点 . 所以点就是所求作的线段的中点.

 (1)、请你根据作法用尺规作图将图2补全,保留作图痕迹;(2)、补全以下证明过程:
(1)、请你根据作法用尺规作图将图2补全,保留作图痕迹;(2)、补全以下证明过程:连接 、 ,
由作图可知: ▲ , ▲ ,
∴四边形是平行四边形 ( )
∴点是线段中点 ( )
20. 如图,点在平行四边形的对角线上,且 . 求证: . 21. 如图,中,平分交于点 , 平分交于点 . 请你判断与的数量关系并证明.
21. 如图,中,平分交于点 , 平分交于点 . 请你判断与的数量关系并证明. 22. 已知一次函数的图象与轴交点的横坐标为4,且过点 .
22. 已知一次函数的图象与轴交点的横坐标为4,且过点 . (1)、求一次函数的表达式;(2)、过点作与轴平行的直线,与一次函数函数的图象交于点 , 当线段时,求的取值范围.23. 已知:如图,中,对角线、交于点 , .
(1)、求一次函数的表达式;(2)、过点作与轴平行的直线,与一次函数函数的图象交于点 , 当线段时,求的取值范围.23. 已知:如图,中,对角线、交于点 , . (1)、求证:四边形 是矩形;(2)、如图,为射线,过点作射线于点 , 连接、 . 请你补全图形,判断与的数量关系,并证明.24. 某蔬菜商人需要租赁货车运输蔬菜,经了解,当地运输公司有大、小两种型 号货车,其租金和运力如下表:
(1)、求证:四边形 是矩形;(2)、如图,为射线,过点作射线于点 , 连接、 . 请你补全图形,判断与的数量关系,并证明.24. 某蔬菜商人需要租赁货车运输蔬菜,经了解,当地运输公司有大、小两种型 号货车,其租金和运力如下表:租金 (元/辆)
最大运力 (箱/辆)
大货车
650
50
小货车
560
40
(1)、若该商人计划租用大、小货车共10辆,其中大货车辆,共需付租金元,请写出与的函数关系式;(2)、在(1)的条件下,若这批蔬菜共460箱,所租用的10辆货车可一次将蔬菜全 部运回,请给出最节省费用的租车方案,并求出最低费用.25. 有这样一个问题:探究函数的图象与性质.思宇根据学习函数的经验,对函数的图象与性质进行了探究.下面是思宇的探究过程,请补充完整: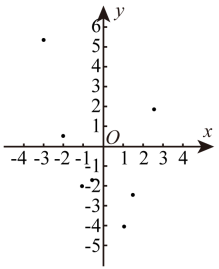 (1)、函数的图象与轴交点;(填写“有”或“无”)(2)、下表是与的几组对应值:
(1)、函数的图象与轴交点;(填写“有”或“无”)(2)、下表是与的几组对应值:…
1
2
…
…
…
则的值为;
(3)、如图,在平面直角坐标系中,思宇描出各对对应值为坐标的点.请你根据描出的点,帮助思宇画出该函数的大致图象;(4)、结合函数的图象,写出该函数的其他性质(一条即可): .26. 如图,在平面直角坐标系中,我们把横、纵坐标都为整数的点叫做整点.一次函数的图像与轴交于点 , 与轴交于点 . (1)、若点的坐标为 , 则的值为;(2)、在(1)的条件下,内的整点有个 (不包括三角形边上的整点);(3)、已知点 , 过点作平行于轴的直线,交直线于点;过点作平行于轴的直线,交直线于点 . 若存在且内(不含三角形的边)没有整点,结合图像求出的取值范围.27. 如图 1,在正方形中,点为边上一点,连接 . 点在边上运动.
(1)、若点的坐标为 , 则的值为;(2)、在(1)的条件下,内的整点有个 (不包括三角形边上的整点);(3)、已知点 , 过点作平行于轴的直线,交直线于点;过点作平行于轴的直线,交直线于点 . 若存在且内(不含三角形的边)没有整点,结合图像求出的取值范围.27. 如图 1,在正方形中,点为边上一点,连接 . 点在边上运动.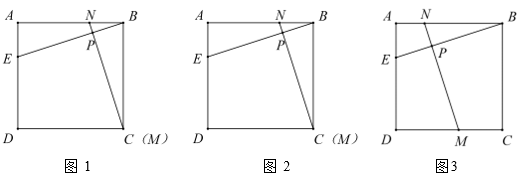
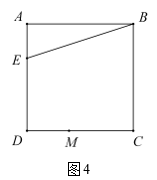 (1)、当点和点重合时(如图2),过点做的垂线,垂足为点 , 交直线于点 . 请直接写出与的数量关系;(2)、当点在边上运动时,过点做的垂线,垂足为点 , 交直线于点(如图 3 ),(1)中的结论依旧成立吗?请证明;(3)、如图 4 ,当点在边上运动时,为直线上一点,若 , 请问是否始终能证明?请你说明理由.28. 在平面直角坐标系中,对于 , 两点给出如下定义:若点的横、纵坐标之和等于点的横、纵坐标之和,则称 , 两点为同和点.下图中的 , 两点即为同和点.
(1)、当点和点重合时(如图2),过点做的垂线,垂足为点 , 交直线于点 . 请直接写出与的数量关系;(2)、当点在边上运动时,过点做的垂线,垂足为点 , 交直线于点(如图 3 ),(1)中的结论依旧成立吗?请证明;(3)、如图 4 ,当点在边上运动时,为直线上一点,若 , 请问是否始终能证明?请你说明理由.28. 在平面直角坐标系中,对于 , 两点给出如下定义:若点的横、纵坐标之和等于点的横、纵坐标之和,则称 , 两点为同和点.下图中的 , 两点即为同和点.
 (1)、已知点的坐标为 .
(1)、已知点的坐标为 .①在点 , , 中,为点的同和点的是;
②若点在轴上,且 , 两点为同和点,则点的坐标为;
(2)、直线与轴、轴分别交于点 , , 点为线段上一点.①若点与点为同和点,求点坐标;
②若存在点与点为同和点,求的取值范围.