安徽省滁州市定远县吴圩片2021-2022学年八年级下学期期中考试数学试题

试卷更新日期：2022-05-26 类型：期中考试

进入出卷网下载

一、单选题

1. 化简后，与 $\sqrt{2}$ 的被开方数相同的二次根式是（）

A、 $\sqrt{12}$ B、 $\sqrt{18}$ C、 $\sqrt{\frac{1}{4}}$ D、 $\sqrt{\frac{2}{3}}$

查看试题解析
2. 已知关于x的方程mx²+2x﹣1＝0有实数根，则m的取值范围是（）

A、m≥﹣1 B、m≤1 C、m≥﹣1且m≠0 D、m≤1且m≠0

查看试题解析
3. 当 $a < 1$ 时，化简 $\sqrt{- a^{3} (1 - a)}$ 的结果是（）

A、 $a \sqrt{(a - 1)}$ B、 $- a \sqrt{a (a - 1)}$ C、 $a \sqrt{a (- a)}$ D、 $- a \sqrt{a (- a)}$

查看试题解析
4. 如图所示：是一段楼梯，高BC是3m，斜边AC是5m，如果在楼梯上铺地毯，那么至少需要地毯（）

A、5m B、6m C、7m D、8m

查看试题解析
5. 下面对关于 $x$ 的一元二次方程 $a (x - 1)^{2} = 2 x^{2} - 2$ 的表述错误的是（）

A、判别式的值为16 B、方程有一根是1 C、a不等于0 D、a不等于2

查看试题解析
6. $\sqrt{5}$ 是一个无理数，则下列判断正确的是（）

A、1＜ $\sqrt{5}$ -1＜2 B、2＜ $\sqrt{5}$ -1＜3 C、3＜ $\sqrt{5}$ -1＜4 D、4＜ $\sqrt{5}$ -1＜5

查看试题解析
7. 如图，a、b、c分别表示直角三角形的三边向外作的正方形的面积，下列关系正确的是（）

A、a+b=c B、a²+b²=c² C、ab=c D、a+b=c²

查看试题解析
8. 一本书共280页，小颖要用14天把它读完，当她读了一半时，发现平均每天需多读21页才能恰好在规定的时间内读完，如果读前一半时，小颖平均每天读x页，则下列方程中正确的是（）

A、 $\frac{140}{x} + \frac{140}{x - 21} = 14$ B、 $\frac{200}{x} + \frac{80}{x + 21} = 14$ C、 $\frac{280}{x} + \frac{280}{x + 21} = 14$ D、 $\frac{140}{x} + \frac{140}{x + 21} = 14$

查看试题解析
9. 关于x的一元二次方程x²﹣mx+（m﹣2）=0的根的情况是（）

A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、无法确定

查看试题解析
10. 如图，点 $P$ 是矩形 $A B C D$ 的对角线 $B D$ 上的点，点 $M$ ， $N$ 分别是 $A B$ ， $A D$ 的中点，连接 $P M$ ， $P N$ .若 $A B = 2$ ， $B D = 4$ ，则 $P M + P N$ 的最小值为（）

A、 $\sqrt{7}$ B、2 C、 $2 + \sqrt{2}$ D、 $1 + \sqrt{3}$

查看试题解析

二、填空题

11. 函数y= $\frac{\sqrt{x - 1}}{x - 2}$ 中，自变量x的取值范围是.

查看试题解析
12. 若一元二次方程2x²﹣3x+1＝0的两个实数根为x₁ ， x₂ ，则x₁²+x₂²﹣x₁•x₂的值是．

查看试题解析
13. 如图，将一根长9cm 的筷子，置于底面直径为3cm，高为4cm的圆柱形水杯中，设筷子露在杯子外面的长度是为hcm ，则h的取值范围是．

查看试题解析
14. 如图，在△ABC中，BC=8，AC=6，AB=10，它们的中点分别是D、E、F，则CF=

查看试题解析

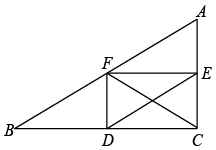
三、解答题

15. 计算

(1)、 $\sqrt{18} - \sqrt{8} + (\sqrt{3} + 1) (\sqrt{3} - 1)$ ；

(2)、 $\sqrt{18}$ ﹣ $\sqrt{\frac{9}{2}}$ +（ $\sqrt{3}$ ﹣2）⁰+ $\sqrt{(1 - \sqrt{2})^{2}}$ ．

查看试题解析
16. 解下列方程：

(1)、 $3 x^{2} - 5 x + 2 = 0$ ；

(2)、 $(y + 1) (y - 1) = 2 y - 1$ ．

查看试题解析
17. 关于 $x$ 的一元二次方程 $x^{2} - (k + 3) x + 2 k + 2 = 0$ .

(1)、求证：方程总有两个实数根；

(2)、若方程有一根小于1，求 $k$ 的取值范围.

查看试题解析
18. 在一条东西走向河的一侧有一村庄C，河边原有两个取水点A，B，其中 $A B = B C$ ，由于某种原因，由C到B的路现在已经不通，该村为方便村民取水决定在河边新建一个取水点D(A、D、B)在同一条直线上)，并新修一条路CD，测得 $C A = 6.5$ 千米， $C D = 6$ 千米， $A D = 2.5$ 千米.

(1)、问CD是否为从村庄C到河边最近的路？请通过计算加以说明：

(2)、求原来的路线 $B C$ 的长.

查看试题解析
19. 已知关于 $x$ 的一元二次方程 $m x^{2} - (m - 3) x - 3 = 0 (m \neq 0)$

(1)、求证：该方程一定有实数根；

(2)、若该方程有两个不相等的整数根，求整数 $m$ 的值．

查看试题解析
20. 我市茶叶专卖店销售某品牌茶叶，其进价为每千克240元，按每千克400元出售，平均每周可售出200千克，后来经过市场调查发现，单价每降低10元，则平均每周的销售量可增加40千克．若该专卖店销售这种品牌茶叶要想平均每周获利41600元，在平均每周获利不变的情况下，为尽可能让利于顾客，赢得市场，每千克茶叶应降价多少元？

查看试题解析
21. 如图，△ACB和△ECD都是等腰直角三角形，∠ACB=∠ECD=90°，D为AB边上一点，求证：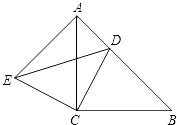

(1)、△ACE≌△BCD；

(2)、AD²+DB²=DE² ．

查看试题解析
22. 如图1，图2分别是某种型号拉杆箱的实物图与示意图，根据商品介绍，获得了如下信息：滑竿DE、箱长BC拉杆AB的长度都相等，即DE=BC=AB=50，点B、F在线段AC上，点C在DE上，支杆DF=30cm．

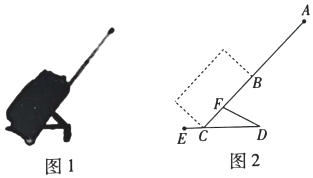(1)、若EC=36cm时，B，D相距48cm，试判定BD与DE的位置关系，并说明理由；

(2)、当∠DCF＝45°，CF＝ $\frac{1}{5}$ AC时，求CD的长．

查看试题解析
23. 菱形ABCD中，∠ABC= 60°，ΔAEF的顶点E、F分别在 BC、CD上．

(1)、如图1，当∠EAF = 60° 时，若AB = 6，BE =2，求AF的长；

(2)、如图2，若点M、N分别为BC、EF的中点，E在点B、M之间，当∠AEF = 60° 时，连接MN并延长交AC于点K，求证：MK⊥AC；

(3)、如图3，在（2）的条件下，当点E与点M重合时，过AC上一点G，作GH⊥AF于点H，连接CH并延长至点P，使得∠BGP =120°，连接BP交AF于点Q．当QH=GH时，请直接写出 $\frac{C G}{B P}$ 的值．

查看试题解析