2022年苏科版初中数学七年级上册 2.3 数轴(1) 同步练习
试卷更新日期:2022-05-25 类型:同步测试
一、夯实基础
-
1. 下列各图中,表示数轴正确的是( )A、
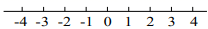 B、
B、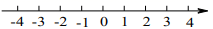 C、
C、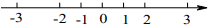 D、
D、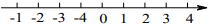 2. 如图,数轴上点M所表示的数可能是( )
2. 如图,数轴上点M所表示的数可能是( )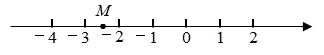 A、3.5 B、-3.5 C、2.5 D、-2.53. 数轴上表示 的点与表示 的点的距离是( )A、-8 B、-2 C、 D、84. 下面的数轴被墨迹盖住一部分,被盖住的整数有( )个
A、3.5 B、-3.5 C、2.5 D、-2.53. 数轴上表示 的点与表示 的点的距离是( )A、-8 B、-2 C、 D、84. 下面的数轴被墨迹盖住一部分,被盖住的整数有( )个 A、9 B、10 C、11 D、125. 数轴上一动点A向左移动3个单位长度到达点B,再向右移动5个单位长度到达点C.若点C表示的数为1,则点A表示的数为( )A、﹣1 B、﹣2 C、﹣3 D、36. 一只蚂蚁从数轴上点A出发向左爬了5个单位长度到了表示-2的点处,则点A所表示的数是.7. 在数轴上,到﹣2的距离等于4个单位长度的点所表示的数是 .8. 请你画一条数轴,并把2,-1,0, , 这五个数在数轴上表示出来.9. 已知:如图在数轴上有 四个点:
A、9 B、10 C、11 D、125. 数轴上一动点A向左移动3个单位长度到达点B,再向右移动5个单位长度到达点C.若点C表示的数为1,则点A表示的数为( )A、﹣1 B、﹣2 C、﹣3 D、36. 一只蚂蚁从数轴上点A出发向左爬了5个单位长度到了表示-2的点处,则点A所表示的数是.7. 在数轴上,到﹣2的距离等于4个单位长度的点所表示的数是 .8. 请你画一条数轴,并把2,-1,0, , 这五个数在数轴上表示出来.9. 已知:如图在数轴上有 四个点: (1)、请写出 分别表示什么数?(2)、在数轴上表示出 的点.
(1)、请写出 分别表示什么数?(2)、在数轴上表示出 的点.二、能力提优
-
10. 如图,用数轴上点M表示有理数2,则表示有理数6的点是( )
 A、A B、B C、C D、D11. 数轴上与表示2的点距离等于3个单位长度的点表示的数是( )A、0或5 B、﹣1或5 C、﹣1或﹣5 D、﹣2或512. 如图,在数轴上有A,B,C,D四个点,分别表示不同的四个数,若从这四点中选一点做原点,使得其余三点表示的数中有两个负数和一个正数,则这个点是( )
A、A B、B C、C D、D11. 数轴上与表示2的点距离等于3个单位长度的点表示的数是( )A、0或5 B、﹣1或5 C、﹣1或﹣5 D、﹣2或512. 如图,在数轴上有A,B,C,D四个点,分别表示不同的四个数,若从这四点中选一点做原点,使得其余三点表示的数中有两个负数和一个正数,则这个点是( ) A、点A B、点B C、点C D、点D13. 数轴上A点表示的数为4,点B与点A位于原点两侧且到原点的距离相等,点C与点B的距离为5,则点C表示的数为.14. 一滴墨水洒在一个数轴上,根据图中标出的数值,判断墨迹盖住的整数个数是个.
A、点A B、点B C、点C D、点D13. 数轴上A点表示的数为4,点B与点A位于原点两侧且到原点的距离相等,点C与点B的距离为5,则点C表示的数为.14. 一滴墨水洒在一个数轴上,根据图中标出的数值,判断墨迹盖住的整数个数是个. 15. 如图,将一刻度尺放在数轴上(数轴上的单位长度是),刻度尺上“”和“”分别对应数轴上的和 , 那么的值为.
15. 如图,将一刻度尺放在数轴上(数轴上的单位长度是),刻度尺上“”和“”分别对应数轴上的和 , 那么的值为.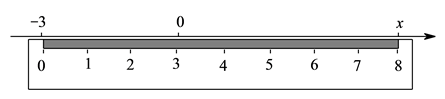 16. 数轴上表示整数的点称为整点.某数轴的单位长度是1厘米,若在这个数轴上随意画出一条长为2013厘米的线段AB,则线段AB盖住的整点的个数是( )A、2011或2012 B、2012或2013 C、2013或2014 D、2014或201517. 已知快递公司坐落在一条东西走向的街道上,某快递员从快递公司取件后在这条街道上送快递,他先向东骑行1千米到达A店,继续向东骑行2千米到达B店,然后向西骑行5千米到达C店,最后回到快递公司。(1)、以快递公司为原点,以向东方向为正方向,用1厘米表示1千米,画出数轴,并在数轴上表示出A,B,C三个店的位置。(2)、C店离A店有多远?(3)、快递员一共骑行了多少千米?18. 操作探究:已知在纸面上有一数轴(如图所示),
16. 数轴上表示整数的点称为整点.某数轴的单位长度是1厘米,若在这个数轴上随意画出一条长为2013厘米的线段AB,则线段AB盖住的整点的个数是( )A、2011或2012 B、2012或2013 C、2013或2014 D、2014或201517. 已知快递公司坐落在一条东西走向的街道上,某快递员从快递公司取件后在这条街道上送快递,他先向东骑行1千米到达A店,继续向东骑行2千米到达B店,然后向西骑行5千米到达C店,最后回到快递公司。(1)、以快递公司为原点,以向东方向为正方向,用1厘米表示1千米,画出数轴,并在数轴上表示出A,B,C三个店的位置。(2)、C店离A店有多远?(3)、快递员一共骑行了多少千米?18. 操作探究:已知在纸面上有一数轴(如图所示),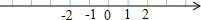
操作一:
⑴折叠纸面,使表示的1点与-1表示的点重合,则-3表示的点与 ▲ 表示的点重合;
操作二:
⑵折叠纸面,使-1表示的点与3表示的点重合,回答以下问题:
①5表示的点与数 ▲ 表示的点重合;
②若数轴上A、B两点之间距离为11,(A在B的左侧),且A、B两点经折叠后重合,求A、B两点表示的数是多少.
三、延伸拓展
-
19.
-2和2对应的点将数轴分成3段,如果数轴上任意n个不同的点中至少有3个在其中之一段,那么n的最小值是 。
 A、5 B、6 C、7 D、820. 点A,B是数轴上两点,位置如图,点P,Q是数轴上两动点,点P由点A点出发,以1单位长度/秒的速度在数轴上运动,点Q由点B点出发,以2单位长度/秒的速度在数轴上运动.若两点同时开始和结束运动,设运动时间为t秒.下面是四位同学的判断:
A、5 B、6 C、7 D、820. 点A,B是数轴上两点,位置如图,点P,Q是数轴上两动点,点P由点A点出发,以1单位长度/秒的速度在数轴上运动,点Q由点B点出发,以2单位长度/秒的速度在数轴上运动.若两点同时开始和结束运动,设运动时间为t秒.下面是四位同学的判断:①小康同学:当t=2时,点P和点Q重合.
②小柔同学:当t=6时,点P和点Q重合.
③小议同学:当t=2时,PQ=8.
④小科同学:当t=6时,PQ=18.
以上说法可能正确的是( )
 A、①②③ B、②③④ C、①③④ D、①②③④21. 定义:数轴上的三点,如果其中一个点与近点距离是它与远点距离的 ,则称该点是其他两个点的“倍分点”.例如数轴上点A,B,C所表示的数分别为﹣1,0,2,满足AB= BC,此时点B是点A,C的“倍分点”.已知点A,B,C,M,N在数轴上所表示的数如图所示.
A、①②③ B、②③④ C、①③④ D、①②③④21. 定义:数轴上的三点,如果其中一个点与近点距离是它与远点距离的 ,则称该点是其他两个点的“倍分点”.例如数轴上点A,B,C所表示的数分别为﹣1,0,2,满足AB= BC,此时点B是点A,C的“倍分点”.已知点A,B,C,M,N在数轴上所表示的数如图所示.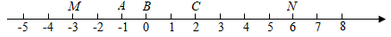 (1)、A,B,C三点中,点是点M,N的“倍分点”;(2)、若数轴上点M是点D,A的“倍分点”,则点D对应的数有个,分别是;(3)、若数轴上点N是点P,M的“倍分点”,且点P在点N的右侧,求此时点P表示的数.
(1)、A,B,C三点中,点是点M,N的“倍分点”;(2)、若数轴上点M是点D,A的“倍分点”,则点D对应的数有个,分别是;(3)、若数轴上点N是点P,M的“倍分点”,且点P在点N的右侧,求此时点P表示的数.