浙江省金华市兰溪市2022年九年级中考模拟数学试卷
试卷更新日期:2022-05-24 类型:中考模拟
一、单选题
-
1. ﹣2022的相反数是( )A、﹣2022 B、2022 C、﹣ D、2. 下列计算错误的是( )A、 B、 C、 D、3. 根据(浙江省)金华市第七次人口普查主要数据公报显示,兰溪市常住人口为574801人,574801这个数用科学记数法(精确到万位)表示为( )A、 B、 C、 D、4. 一个不透明的袋子里有若干张2022年北京冬奥会宣传卡片,其中3张卡片印有会徽图案、4张卡片印有吉祥物冰墩墩图案、2张卡片印有吉祥物雪容融图案,每张卡片只有一种图案,它们除图案不同外其余均相同,从中随机摸出1张卡片,则印有冰墩墩图案的概率是( )A、 B、 C、 D、5. 将抛物线 向下平移3个单位,则平移后的抛物线表达式为( )A、 B、 C、 D、6. 小明从A处出发沿北偏东50°方向行走至B处,又从B处沿南偏东70°方向行走至C处,则∠ABC等于( )A、20° B、100° C、120° D、160°7. 如图,△ABC内接于⊙O,若∠A=45°,OC=2,则BC的长为( )
 A、 B、 C、 D、28. 解方程 , 以下去分母正确的是 ( ).A、 B、 C、 D、9. 方程 的根可视为函数 的图象与函数 的图象交点的横坐标,那么用此方法可推断出方程 的实数根x所在的范围是( )A、 B、 C、 D、10. 如图,在平面直角坐标系中,已知 ,四边形ABCD和AEFG都是正方形,点A、D、E共线,点G、A、B在x轴上,点C,E,F在以O为圆心OC为半径的圆上,则 的长为( ).
A、 B、 C、 D、28. 解方程 , 以下去分母正确的是 ( ).A、 B、 C、 D、9. 方程 的根可视为函数 的图象与函数 的图象交点的横坐标,那么用此方法可推断出方程 的实数根x所在的范围是( )A、 B、 C、 D、10. 如图,在平面直角坐标系中,已知 ,四边形ABCD和AEFG都是正方形,点A、D、E共线,点G、A、B在x轴上,点C,E,F在以O为圆心OC为半径的圆上,则 的长为( ).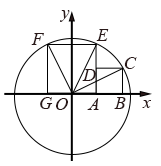 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 分解因式4x2﹣4x+1=.12. 当 时,二次根式 的值是.13. 兰溪市某校九年级举办“消防知识”竞赛,参赛同学的决赛成绩统计图如图所示,则该决赛成绩的平均分为分.
 14. 已知抛物线 , ,若这两个抛物线与x轴共有3个交点,则a的值为.15. 如图,用8个全等的Rt△ABC (AC >BC) 分别拼成如图1和图2中的两个正方形,中间的两个小正方形的面积分别记为 和 ,且 , 则tanA=.
14. 已知抛物线 , ,若这两个抛物线与x轴共有3个交点,则a的值为.15. 如图,用8个全等的Rt△ABC (AC >BC) 分别拼成如图1和图2中的两个正方形,中间的两个小正方形的面积分别记为 和 ,且 , 则tanA=. 16. 如图1所示的是古代一种可以远程攻击的投石车,图2是投石车投石过程中某时刻的示意图,GP是杠杆,弹袋挂在点G,重锤挂在点P,点A为支点,点D是水平底板BC上的一点,AD=AC=3米,CD=3.6米.
16. 如图1所示的是古代一种可以远程攻击的投石车,图2是投石车投石过程中某时刻的示意图,GP是杠杆,弹袋挂在点G,重锤挂在点P,点A为支点,点D是水平底板BC上的一点,AD=AC=3米,CD=3.6米.
 (1)、投石车准备时,点G恰好与点B重合,此时AG和AC垂直,则AG=米.(2)、投石车投石瞬间,AP的延长线交线段DC于点E,若 ,则点G的上升高度为米.
(1)、投石车准备时,点G恰好与点B重合,此时AG和AC垂直,则AG=米.(2)、投石车投石瞬间,AP的延长线交线段DC于点E,若 ,则点G的上升高度为米.三、解答题
-
17. 计算: .18. 解不等式组19. 某市为了将生活垃圾合理分类,并更好地回收利用,将垃圾分为可回收物、厨余垃圾、有害垃圾和其他垃圾四类.现随机抽取该市 吨垃圾,将调查结果制成如下两幅不完整的统计图:

根据统计图提供的信息,解答下列问题:
(1)、 , .(2)、扇形统计图中,求厨余垃圾所对应的扇形圆心角的度数;(3)、根据抽样调查的结果,请你估计该市2000吨垃圾中约有多少吨可回收物.20. 如图,“爱心”图案是由抛物线 的一部分及其关于直线y=x的对称图形组成,点A、B是“爱心”图案与其对称轴的两个交点,点C、D、E、F是图案与坐标轴的交点,且点C的坐标为 .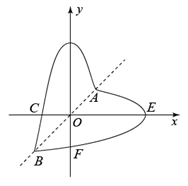 (1)、求k的值及DF的长.(2)、求AB的长.21. 如图,AB为⊙O的直径,延长AB至点D,CD切⊙O于点C,点B是 的中点,弦CF交AB于点E,连结OF、BC,过B点作BG⊥CD于点G.
(1)、求k的值及DF的长.(2)、求AB的长.21. 如图,AB为⊙O的直径,延长AB至点D,CD切⊙O于点C,点B是 的中点,弦CF交AB于点E,连结OF、BC,过B点作BG⊥CD于点G.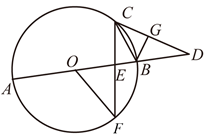 (1)、若∠BCD=28°,求∠F的度数.(2)、若CF=4OE,⊙O的半径为 ,求BG的长.22. 如图1是城市平直道路,道路限速60km/h,A路口停车线 和B路口停车线 之间相距S=400m,A、B两路口各有一个红绿灯.在停车线 后面停着一辆汽车,该汽车的车头恰好与停车线 平齐,已知汽车启动后开始加速,加速后汽车行驶的路程S、速度v与时间t的关系分别可以用二次函数和一次函数表示,其图象如图2、3所示.某时刻A路口绿灯亮起,该汽车立即启动.(车身长忽略不计)
(1)、若∠BCD=28°,求∠F的度数.(2)、若CF=4OE,⊙O的半径为 ,求BG的长.22. 如图1是城市平直道路,道路限速60km/h,A路口停车线 和B路口停车线 之间相距S=400m,A、B两路口各有一个红绿灯.在停车线 后面停着一辆汽车,该汽车的车头恰好与停车线 平齐,已知汽车启动后开始加速,加速后汽车行驶的路程S、速度v与时间t的关系分别可以用二次函数和一次函数表示,其图象如图2、3所示.某时刻A路口绿灯亮起,该汽车立即启动.(车身长忽略不计) (1)、求该汽车从停车线 出发加速到限速所需的时间.(2)、求该汽车最快需要多少时间可以通过停车线 .(3)、若A路口绿灯亮起29s后B路口绿灯亮起,且B路口绿灯的持续时间为23s.该汽车先加速行驶,然后一直匀速行驶.若该汽车在B路口绿灯期间能顺利通过停车线 ,求该汽车匀速行驶过程中速度的取值范围.23. 如图1,点A是函数 的图象上一动点,连结OA交函数 的图象于点B,过B作x轴的平行线交函数 的图象于点C,连结AC并延长交x轴于点D.设点B的横坐标为m.
(1)、求该汽车从停车线 出发加速到限速所需的时间.(2)、求该汽车最快需要多少时间可以通过停车线 .(3)、若A路口绿灯亮起29s后B路口绿灯亮起,且B路口绿灯的持续时间为23s.该汽车先加速行驶,然后一直匀速行驶.若该汽车在B路口绿灯期间能顺利通过停车线 ,求该汽车匀速行驶过程中速度的取值范围.23. 如图1,点A是函数 的图象上一动点,连结OA交函数 的图象于点B,过B作x轴的平行线交函数 的图象于点C,连结AC并延长交x轴于点D.设点B的横坐标为m.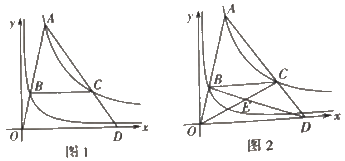 (1)、若m=2,则点A的坐标是.(2)、连结OC,若△AOC是以AC为底边的等腰三角形,求m的值.(3)、如图2,连结OC,BD,相交于点E,在点A向右运动的过程中,四边形ABEC的面积会变吗?如果会,请说明理由,如果不会,请求出它的面积.24. 如图1,在平面直角坐标系中,点A、点B分别是x轴、y轴正半轴上的点,以OA、OB为边构造矩形OACB.点E为OA上一点,满足BE=BC.过点C作CF⊥BE,垂足为点F.已知 .
(1)、若m=2,则点A的坐标是.(2)、连结OC,若△AOC是以AC为底边的等腰三角形,求m的值.(3)、如图2,连结OC,BD,相交于点E,在点A向右运动的过程中,四边形ABEC的面积会变吗?如果会,请说明理由,如果不会,请求出它的面积.24. 如图1,在平面直角坐标系中,点A、点B分别是x轴、y轴正半轴上的点,以OA、OB为边构造矩形OACB.点E为OA上一点,满足BE=BC.过点C作CF⊥BE,垂足为点F.已知 .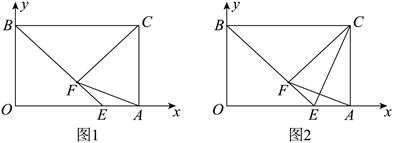 (1)、求证:CA=CF.(2)、如图2,连结CE,当∠BCF=2∠ECF时,求AE的长.(3)、在(2)的条件下,连结AF,在坐标平面内是否存在一点M,使得以点M、A、F为顶点的三角形与△CBE相似?若存在,请求出点M的坐标;若不存在,请说明理由.
(1)、求证:CA=CF.(2)、如图2,连结CE,当∠BCF=2∠ECF时,求AE的长.(3)、在(2)的条件下,连结AF,在坐标平面内是否存在一点M,使得以点M、A、F为顶点的三角形与△CBE相似?若存在,请求出点M的坐标;若不存在,请说明理由.