浙江省杭州市萧山区2022年初中毕业文化监测一模数学试卷

试卷更新日期：2022-05-24 类型：中考模拟

进入出卷网下载

一、单选题

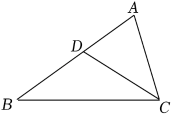
1. 有理数2022的相反数是（）

A、2022 B、-2022 C、 $\frac{1}{2022}$ D、 $- \frac{1}{2022}$

查看试题解析
2. 2022年1月28日，北京冬奥组委发布《北京冬奥会低碳管理报告（赛前）》，根据本次“绿色办奥”理念，以及疫情下筹办和举办北京冬奥会的实际情况，修订后的基准线排放量约为130.6万吨二氧化碳当量，其中“130.6万”用科学记数法表示为（）

A、 $13.06 \times 1 0^{5}$ B、 $130.6 \times 1 0^{4}$ C、 $1.306 \times 1 0^{6}$ D、 $1.306 \times 1 0^{5}$

查看试题解析
3. 下列因式分解正确的是（）

A、 $a^{3} b - a b = a b (a^{2} - 1)$ B、 $x^{2} - 2 x + 4 = {(x - 2)}^{2}$ C、 $- 9 + y^{2} = (3 + y) (y - 3)$ D、 $4 a^{2} - b^{2} = (4 a + b) (4 a - b)$

查看试题解析
4. 下列计算正确的是（）

A、 $2^{2} + 2^{3} = 2^{5}$ B、 $2^{3} - 2^{2} = 2$ C、 $2^{3} \cdot 2^{2} = 2^{5}$ D、 $2^{- 1} = - 2$

查看试题解析
5. 如图，在△ABC中，∠ACB＝2∠B，CD平分∠ACB，AD＝2，BD＝3，则AC的长为（）

A、3 B、 $\sqrt{10}$ C、4 D、 $2 \sqrt{3}$

查看试题解析
6. "桃花流水窅然去，别有天地非人间."桃花园景点2017年三月共接待游客 $a$ 万人，2018年三月比2017年三月旅游人数增加5%，已知2017年三月至2019年三月欣赏桃花的游客人数平均年增长率为8%，设2019年三月比2018年三月游客人数增加 $b %$ ，则可列方程为（）

A、 $a (1 + 5 %) (1 + b %) = a (1 + 8 % \times 2)$ B、 $a (1 + 5 %) (1 + b %) = a {(1 + 8 %)}^{2}$ C、 $a (1 + 5 %) (1 + 8 %) = a (1 + b % \times 2)$ D、 $a (1 + 5 %) (1 + 8 %) = 2 a (1 + b %)$

查看试题解析
7. 将分别标有“中”“国”…“全”“面”“小”“康”汉字的六个小球装在一个不透明的口袋中，这些球除汉字外无其他差别，每次摸球前先搅拌均匀，随机摸出一球，然后放回，再随机摸出一球，两次摸出的球上的汉字是“小”和“康”的概率是（）

A、 $\frac{1}{4}$ B、 $\frac{1}{6}$ C、 $\frac{1}{9}$ D、 $\frac{1}{18}$

查看试题解析
8. 当 $1 \leq x \leq 3$ 时，二次函数 $y = x^{2} - 2 a x + 3$ 的最小值为-1，则 $a$ 的值为（）

A、2 B、±2 C、2 或 $\frac{5}{2}$ D、2 或 $\frac{13}{6}$

查看试题解析
9. 图1是第七届国际数学教育大会(ICME)的会徽，主体图案是由如图2的一连串直角三角形演化而成，其中 $O A_{1} = A_{1} A_{2} = A_{2} A_{3} = \cdot \cdot \cdot = A_{8} A_{9} = 1$ ，现把图2中的直角三角形继续作下去如图3所示，若 $O A_{3} \cdot O A_{n}$ 的值是整数，且1≤n≤30，则符合条件的n有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
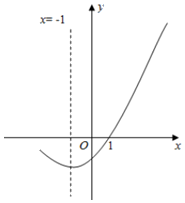
10. 如图，二次函数y＝ax²+bx+c（a≠0）图象的一部分与x轴的一个交点坐标为（1，0），对称轴为直线x＝﹣1，结合图象给出下列结论：
①a+b+c＝0；②a﹣2b+c＞0；③关于x的一元二次方程ax²+bx+c＝0（a≠0）的两根分别为3和1；④若点（﹣4，y₁），（﹣2，y₂），（3，y₃）均在二次函数图象上，则y₁＜y₂＜y₃；⑤a﹣b＜m（am+b）（m为任意实数）．
其中正确的结论有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

11. 计算： $\sqrt{8} - 2 c o s 45 ° =$ ．

查看试题解析
12. 解方程： $\frac{1}{x - 2} = 1$ 的解是 $x =$ .

查看试题解析
13. 已知数据x₁ ， x₂ ， ....，x_n的方差为3，则数据2x₁﹣7，2x₂﹣7，…，2x_n﹣7的方差为．

查看试题解析
14. 春节期间，某超市推出了甲、乙、丙三种腊味套盒，各套盒均含有香肠、腊肉、腊排骨、腊猪脚等四种腊味各若干袋，每袋腊味的重量为500克，一袋腊肉的售价不低于30元，一袋香肠的售价比一袋腊肉的售价贵，单袋腊味的售价均为整数元，套盒的售价即为单袋腊味的售价之和，甲套盒中含有香肠2袋，腊肉5袋，腊排骨2袋，腊猪脚2袋，乙套盒中含有香肠4袋，腊肉5袋，腊排骨1袋，腊猪脚1袋，丙套盒中含有香肠3袋，腊肉5袋，腊排骨2袋，腊猪脚1袋，甲、乙礼盒售价均为415元，丙礼盒售价比甲礼盒贵10元，则腊排骨每袋元.

查看试题解析
15. 如图，已知⊙O上有三点A、B、C，半径OC＝2，∠ABC＝30°，切线AP交OC延长线于点P，则△OAP的周长为

查看试题解析
16. 如图，正方形 $A B C D$ 的边长为4，点E是对角线 $A C$ 上的动点（点E不与A，C重合），连接 $B E ， E F ⊥ B E$ 交 $C D$ 于点F，线段 $E F$ 绕点F逆时针旋转 $90 °$ 得到线段 $F G$ ，连接 $B G$ ．下列结论：① $B E = E F$ ；② $∠ A C G = 90 °$ ；③若四边形 $B E F G$ 的面积是正方形 $A B C D$ 面积的一半，则 $A E$ 的长为 $4 \sqrt{2} - 4$ ；④ $C G + C E = \sqrt{2} A B$ ．其中正确的是．（填写所有正确结论的序号）

查看试题解析

三、解答题

17. 解不等式组 ${\begin{array}{l} 5 x - 1 < 3 (x + 1) \\ \frac{2 x - 1}{3} - \frac{5 x + 1}{2} ⩽ 1 \end{array}$ ，并把它们的解集表示在数轴上．

查看试题解析
18. 已知：Rt $△$ ABC中，∠B＝90°，D是BC上一点，DF⊥BC交AC于点H，且DF＝BC，FG⊥AC交BC于点E.求证：AB＝DE.

查看试题解析
19. 疫情当前，为了贯彻落实教育部关于“停课不停学”的要求，某市为学生提供以下四类在线学习方式：腾讯课堂，钉钉在线课堂，校讯通以及名校同步课堂.为了解决学生需求，该市随机对部分学生发起了“你对哪类在线学习方式最感兴趣？”的调查问卷，并根据调查结果绘制出如图两幅不完整的统计图，请你根据图中提供的信息解决下列问题：

(1)、在这次调查中，一共抽取了名学生；

(2)、请你补全条形统计图；

(3)、m=；n=；

(4)、某校共有学生2000人，请你估计该校对“名校同步课堂”最感兴趣的学生有多少名？

查看试题解析
20. 享有“安徽第一楼”之称的安徽省国际金融大厦，它由高度不同的两座楼组成，如图，从左楼顶C处测得右楼楼顶A处的仰角为60°，在左楼楼底D处测得A处的仰角为75°，已知左楼CD高126米，请你利用已知数据估算右楼AB的高．（结果精确到1米， $\sqrt{3}$ ≈1.7）

查看试题解析
21. 如图，直线 $l_{1}$ 分别与x轴，y轴交于A､B两点，A､B的坐标分别为 $(2 ， 0)$ 、 $(0 ， 3)$ ，过点B的直线 $l_{2} ： y = \frac{1}{2} x + 3$ 交x轴于点C，点 $D (n ， 6)$ 是直线l上的一点，连接 $C D$ ．

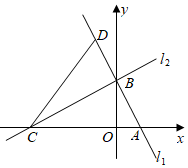(1)、求 $l_{1}$ 的解析式；

(2)、求C､D的坐标；

(3)、求 $△ B C D$ 的面积．

查看试题解析
22. 已知抛物线 $y = a {(x - 1)}^{2} + 3 a$ ，其顶点为 $E$ ，与 $y$ 轴交于点 $D (0 ， 4)$ ．

(1)、求抛物线的解析式；

(2)、若直线 $l$ ： $y = - \frac{1}{3} x + 8$ 与抛物线第一象限交于点 $B$ ，交 $y$ 轴于点 $A$ ，求 $∠ A B D - ∠ D B E$ 的值；

(3)、若有两个定点 $F (1 ， \frac{13}{4})$ ， $A (0 ， 8)$ ，请在抛物线上找一点 $K$ ，使得 $△ K F A$ 的周长最小，并求出周长的最小值．

查看试题解析
23. 已知：如图，在△OAB中，OA=OB，⊙O经过AB的中点C，与OB交于点D，且与BO的延长线交于点E，连接EC，CD．

(1)、试判断AB与⊙O的位置关系，并加以证明；

(2)、若tanE= $\frac{1}{2}$ ，⊙O的半径为3，求OA的长．

查看试题解析