浙江省杭州市上城区2022年中考一模数学试卷

试卷更新日期：2022-05-24 类型：中考模拟

进入出卷网下载

一、单选题

1. 2022年2月5日，杭州某区最高气温为8℃，最低气温为－1℃，那么这天的最高气温比最低气温高（）

A、7℃ B、－7℃ C、9℃ D、－9℃

查看试题解析
2. 下列调查适合抽样调查的是（）

A、某封控区全体人员的核酸检测情况 B、我国“神舟十三号”载人航天飞船各零部件的质量情况 C、审查书稿中的错别字 D、一批节能灯管的使用寿命

查看试题解析
3. 下列代数式相等的是（）

A、 $3 a$ 与 $3 + a$ B、 $a^{4}$ 与 $a^{2} \cdot a^{2}$ C、 $- 3 (a - b)$ 与 $- 3 a - 3 b$ D、 ${(a - 1)}^{2}$ 与 $a^{2} - 1$

查看试题解析
4. 二元一次方程 $4 x - y = 2$ 的解可以是（）

A、 ${\begin{array}{l} x = - 2 \\ y = 10 \end{array}$ B、 ${\begin{array}{l} x = - 1 \\ y = 2 \end{array}$ C、 ${\begin{array}{l} x = 1 \\ y = 2 \end{array}$ D、 ${\begin{array}{l} x = 2 \\ y = - 6 \end{array}$

查看试题解析
5. 某校举行男女混合长跑接力赛，901班为参赛同学买了A，B两款运动服，A款共花费648元，B款共花费500元，A款比B款多2件，A款单价为B款的1.2倍. 若设B款的单价为x元，一根据题意可列方程为（）

A、 $\frac{648}{1.2 x} - \frac{500}{x} = 2$ B、 $\frac{500}{x} - \frac{648}{1.2 x} = 2$ C、 $\frac{500}{1.2 x} - \frac{648}{x} = 2$ D、 $\frac{648}{x} - \frac{500}{1.2 x} = 2$

查看试题解析
6. 在平面直角坐标系中，已知点E（－6，2），F（－2，－2），以原点O为位似中心，位似比为 $\frac{1}{2}$ ，把△EFO缩小，则点F的对应点F′的坐标是（）

A、（－1，－1） B、（1，1） C、（－4，－4）或（4，4） D、（－1，－1）或（1，1）

查看试题解析
7. 如图（1）是2022年杭州亚运会徽标的示意图，若AO＝5，BO＝2，∠AOD＝120°，则阴影部分面积为（）

A、 $14 π$ B、 $7 π$ C、 $\frac{25}{3} π$ D、 $2 π$

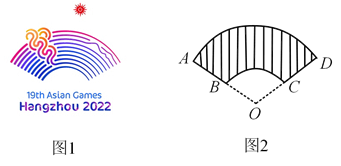查看试题解析
8. 斑马线前“车让人”，反映了城市的文明程度，但行人一般都会在红灯亮起前通过马路，某人行横道全长24米，小明以1.2m/s的速度过该人行横道，行至 $\frac{1}{3}$ 处时，9秒倒计时灯亮了，小明要在红灯亮起前通过马路，他的速度至少要提高到原来的（）

A、1.1倍 B、1.4倍 C、1.5倍 D、1.6倍

查看试题解析
9. 如图，在正方形ABCD内部，以边长为斜边构造两个全等的直角三角形，已知正方形边长为5，较短的直角边长为3，则两个直角顶点之间的距离EF为（）

A、1 B、 $\sqrt{2}$ C、1.5 D、 $\sqrt{3}$

查看试题解析
10. 在直角坐标系中，一次函数 $y = k x + 1 - 2 k (k \neq 0)$ 的图象记作G，以原点O为圆心，作半径为1的圆，有以下几种说法：
①当G与⊙O相交时，y随x增大而增大；②当G与⊙O相切时， $k = \frac{5}{4}$ ③当G与⊙O相离时， $k > \frac{4}{3}$ 或 $k < 0$ . 其中正确的说法是（）

A、① B、①② C、①③ D、②③

查看试题解析

二、填空题

11. 因式分解： $x^{2} - 4 =$ .

查看试题解析
12. 疫情防控期间，杭州市红十字会陆续收到了爱心市民的捐款.某位爱心市民于2022年3月份通过杭红捐赠平台累计捐款6000元3次，3000元2次，8000元1次，5000元4次，则这位爱心市民平均每次捐款元.

查看试题解析
13. 心理学家发现，学生对概念的接受能力y与提出概念所用时间x(分)之间满足关系y=-0.1x ²+2.6x+43(0≤x≤30)，y值越大，表示接受能力越强，在第分钟时，学生接受能力最强.

查看试题解析
14. 如图为《北京2022年冬残奥会会徽》纪念邮票，其规格为边长14.92毫米的正八边形，则正八边形的内角和为.

查看试题解析
15. 如图1，把标准纸（长与宽之比为 $\sqrt{2}$ ）一次又一次对开，按图2叠放，可以发现，这些叠放起来的矩形的右上顶点与左下顶点在同一直线上. 若以图2最大矩形的左下顶点为原点，以宽和长所在直线分别为x轴和y轴，则这组矩形的右上顶点所在直线的函数表达式为.

查看试题解析
16. 两块全等的等腰直角三角板如图放置，∠BAC＝∠EDF＝90°，△DEF的顶点E与△ABC的斜边BC的中点重合，将△DEF绕点E旋转，旋转过程中，当点D落在直线AB上时，若BC＝2，则AD＝.

查看试题解析

三、解答题

17. 计算：

(1)、 $\sqrt{9} + 2^{2} - \sqrt[3]{8}$ ；

(2)、 $\sin 30 ° + \tan 45 °$

查看试题解析
18. 《最强大脑第9季》推出Level K（最高阶思维策略）冲击挑战，其中包含A，B，C，D四个挑战项目，每位选手随机选择其中一个项目参加.

(1)、若选手甲任意选择一个项目，请列出甲选择项目的所有可能情况.

(2)、求选手乙和选手丙选择同一项目的概率.

查看试题解析
19. 如图，AD平分∠BAC，且∠C＝∠D，点E为AD上一点.

(1)、求证：△ABD∽△AEC.

(2)、若AC// BD，AB＝5，AC＝6，CE＝4，求AD的长.

查看试题解析

20. 某同学设计了如下杠杆平衡实验：如图，取一根长65cm的质地，均匀木杆，用细绳绑在木杆的中点O处并将其吊起来，在中点的左侧，距离中点20cm处挂一个重9N的物体，在中点的右侧，用一个弹簧测力计向下拉，使木杆保持平衡（动力×动力臂＝阻力×阻力臂），改变弹簧测力计与中点O的距离L（单位：cm），观察弹簧测力计的示数F（单位：N）. 通过实验，得到下表数据：

	第1组	第2组	第3组	第4组	第5组
L/cm	20	24	25	28	30
F/N	9	7.5	10	6

(1)、你认为表中哪组数据是明显错误的.

(2)、在已学过的函数中选择合适的模型，求F关于L的函数表达式.

(3)、若弹簧测力计的量程是10N，求L的取值范围.

查看试题解析

21. 如图，将Rt△ABC的直角边AC沿过点A的直线折叠，使点C恰好落在斜边AB上.

(1)、请用直尺和圆规作出折痕（只要求作出图形，并保留作图痕迹）.

(2)、若∠B＝50°，求折痕与直角边BC所形成的锐角度数.

查看试题解析
22. 如图1用一个平面截取圆锥，得到的图形可能是圆、椭圆、双曲线，而当平面与圆锥的母线平行，且不过圆锥顶点时，所截得的图形为抛物线，即图2中曲线ACB为抛物线的一部分，交母线于点C，交底面⊙P于点A，B，AB垂直于底面⊙P的直径EF，垂足为点O. 已知底面⊙P的半径为5，OP＝3.

(1)、求弦AB的长.

(2)、以AB所在直线为x轴，OC所在直线为y轴，建立直角坐标系，当OC＝8时，求经过点A，C，B的抛物线的函数表达式.

(3)、若抛物线上有一点H（m，6），求m的值.

查看试题解析
23. 如图1，已知矩形ABCD对角线AC和BD相交于点O，点E是边AB上一点，CE与BD相交于点F，连结OE.

(1)、若点E为AB的中点，求 $\frac{O F}{F B}$ 的值.

(2)、如图2，若点F为OB中点，求证：AE＝2BE.

(3)、如图2，若OE⊥AC，BE＝1，且OF＝k·BF，请用k的代数式表示AC².

查看试题解析