四川省宜宾市叙州区2022年中考数学模拟试卷
试卷更新日期:2022-05-24 类型:中考模拟
一、单选题
-
1. 3≤m≤5,化简|m﹣5|+|2m﹣6|的结果是( )A、 m﹣1 B、1﹣m C、3m﹣11 D、11﹣3m2. “一带一路”涉及沿线65个国家,总涉及人口约4500000000,将4500000000用科学记数法表示为( )A、 B、 C、 D、3. 数据3、3、5、8、11的中位数是( )A、3 B、4 C、5 D、64. 线段AB∥x轴,且AB=3,若点A的坐标为(﹣2,3),则点B的坐标为( )A、(1,3) B、(﹣5,3) C、(1,3)或(﹣5,3) D、(﹣2,0)或(﹣2,6)5. 下列事件是必然事件的为( )A、明天早上会下雨 B、任意一个三角形,它的内角和等于 C、踯一枚硬币,正面朝上 D、打开电视机,正在播放“新闻联播”6. 如图,在△ABC中,AD是边BC上的中线,E是AD的中点,过点E作EF⊥BC于点F.若BC=10,△ABD的面积为24,则EF的长为( )
 A、1.2 B、2.4 C、3.6 D、4.87. 为了治理城市污水,需要铺设一段全长为300米的污水排放管道,铺设120米后,为了尽可能减少施工对城市交通所造成的影响,后来每天的工作量比原来增加20%,结果共用了27天完成了这一任务,求原来每天铺设管道多少米?设原来每天铺设管道x米,所列方程为( )A、 B、 C、 D、8. 如图,⊙O的半径为 ,BD是⊙O的切线,D为切点,过圆上一点C作BD的垂线,垂足为B,BC=3,点A是优弧CD的中点,则sin∠A的值是( )
A、1.2 B、2.4 C、3.6 D、4.87. 为了治理城市污水,需要铺设一段全长为300米的污水排放管道,铺设120米后,为了尽可能减少施工对城市交通所造成的影响,后来每天的工作量比原来增加20%,结果共用了27天完成了这一任务,求原来每天铺设管道多少米?设原来每天铺设管道x米,所列方程为( )A、 B、 C、 D、8. 如图,⊙O的半径为 ,BD是⊙O的切线,D为切点,过圆上一点C作BD的垂线,垂足为B,BC=3,点A是优弧CD的中点,则sin∠A的值是( ) A、 B、 C、 D、9. 设 , 是方程 的两根,则 的值是( )A、0 B、1 C、2000 D、400000010. 下列四个函数图象中,当x>0时,y随x的增大而增大的是( )A、
A、 B、 C、 D、9. 设 , 是方程 的两根,则 的值是( )A、0 B、1 C、2000 D、400000010. 下列四个函数图象中,当x>0时,y随x的增大而增大的是( )A、 B、
B、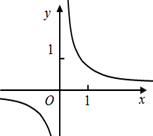 C、
C、 D、
D、 11. 如图,在▱ABCD中,E是AD边上的中点,连接BE,并延长BE交CD的延长线于点F,那么 的值是( )
11. 如图,在▱ABCD中,E是AD边上的中点,连接BE,并延长BE交CD的延长线于点F,那么 的值是( ) A、 B、 C、 D、12. 下表中列出的是一个二次函数 的自变量x与函数y的几组对应值:
A、 B、 C、 D、12. 下表中列出的是一个二次函数 的自变量x与函数y的几组对应值:…
…
…
…
下列各选项中,正确的是( )
A、 B、当 或 时, C、关于x的方程 的解为 D、当 时,y的值随x值的增大而减小二、填空题
-
13. 若 有意义,则m的值可以是.(填一个你喜欢的数)14. 因式分解:xy2﹣4xy+4x= .15. 如果关于x的方程 有两个相等的实数根,那么 的值等于.16. 若不等式组 的解集是 ,则m的取值范围是 .17. 如图,线段OA分别交反比例函数y1= (x>0),y2= (x>0)的图象于点A,B,过点B作CD⊥x轴于点D,交反比例函数y1= (x>0)的图象于点C,若OB=2AB,则△OBD与△ABC的面积之比为.
 18. 如图, 中, , , 于点D,点E是线段CD的一个动点,则 的最小值是.
18. 如图, 中, , , 于点D,点E是线段CD的一个动点,则 的最小值是.
三、解答题
-
19.(1)、计算:2sin60°+ +|2﹣ |﹣ ;(2)、化简: ÷(a﹣ ).20. 为了提高学生身体素质,北关中学开展了课间跑步活动,初三年级针对同学们在这个活动中完成的跑步圈数展开调查,随机抽取了部分学生了解情况,并将调查结果绘制成图1,图2的统计图(未画完整),请结合图中的信息解答下列问题:
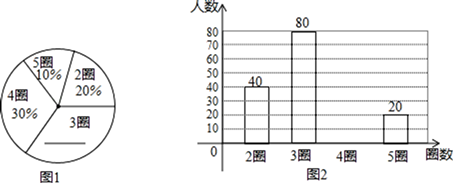 (1)、这次调查中,一共调查了名学生;(2)、请补全两幅统计图;(3)、某班学生有5个跑5圈,其中3名男生,2名女生,现从这5名学生中任意抽取2名来带领其他同学训练,求恰好抽到一男一女的概率.21. 如图,在甲建筑物上从A到E悬挂一条条幅,在乙建筑物顶部D点测得条幅顶端A点的仰角为30º,测得条幅底端E点的俯角为45º,若甲、乙两建筑物之间的水平距离为30米,求条幅AE的长.(结果精确到个位,参考数据 =1.732)
(1)、这次调查中,一共调查了名学生;(2)、请补全两幅统计图;(3)、某班学生有5个跑5圈,其中3名男生,2名女生,现从这5名学生中任意抽取2名来带领其他同学训练,求恰好抽到一男一女的概率.21. 如图,在甲建筑物上从A到E悬挂一条条幅,在乙建筑物顶部D点测得条幅顶端A点的仰角为30º,测得条幅底端E点的俯角为45º,若甲、乙两建筑物之间的水平距离为30米,求条幅AE的长.(结果精确到个位,参考数据 =1.732)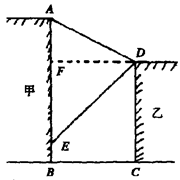 22. 工艺商场按标价销售某种工艺品时,每件可获利45元;按标价的八五折销售该工艺品8件与将标价降低35元销售该工艺品12件所获利润相等.(1)、该工艺品每件的进价、标价分别是多少元?(2)、若每件工艺品按(1)中求得的进价进货,标价售出,工艺商场每天可售出该工艺品100件.若每件工艺品降价1元,则每天可多售出该工艺品4件.问每件工艺品降价多少元出售,每天获得的利润可为4000元且成本较低?23. 如图所示,已知一次函数y=kx+b(k≠0)的图象与反比例函数y= 的图象交于A、B两点,且点A的横坐标和B点的纵坐标都是﹣2,求△AOB的面积.
22. 工艺商场按标价销售某种工艺品时,每件可获利45元;按标价的八五折销售该工艺品8件与将标价降低35元销售该工艺品12件所获利润相等.(1)、该工艺品每件的进价、标价分别是多少元?(2)、若每件工艺品按(1)中求得的进价进货,标价售出,工艺商场每天可售出该工艺品100件.若每件工艺品降价1元,则每天可多售出该工艺品4件.问每件工艺品降价多少元出售,每天获得的利润可为4000元且成本较低?23. 如图所示,已知一次函数y=kx+b(k≠0)的图象与反比例函数y= 的图象交于A、B两点,且点A的横坐标和B点的纵坐标都是﹣2,求△AOB的面积. 24. 如图,AB为的直径,AC平分交于点C, , 垂足为点D.求证:CD是的切线.
24. 如图,AB为的直径,AC平分交于点C, , 垂足为点D.求证:CD是的切线. 25. 如图1,在平面直角坐标系中,抛物线y=ax2-2ax+3与x轴交于点A,B(点A在点B的左侧),交y轴于点C,点A的坐标为(-1,0),点D为抛物线的顶点,对称轴与x轴交于点E.
25. 如图1,在平面直角坐标系中,抛物线y=ax2-2ax+3与x轴交于点A,B(点A在点B的左侧),交y轴于点C,点A的坐标为(-1,0),点D为抛物线的顶点,对称轴与x轴交于点E.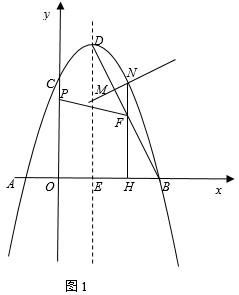
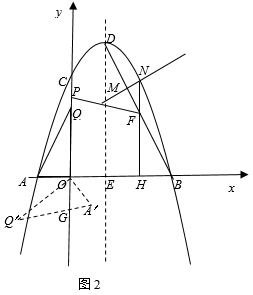 (1)、填空:a= , 点B的坐标是;(2)、连结BD,点M是线段BD上一动点(点M不与端点B,D重合),过点M作MN⊥BD,交抛物线于点N(点N在对称轴的右侧),过点N作NH⊥x轴,垂足为H,交BD于点F,点P是y轴上一动点,当△MNF的周长取得最大值时,求FP+ PC的最小值;(3)、在(2)中,当△MNF的周长取得最大值时,FP+ PC取得最小值时,如图2,把点P向下平移 个单位得到点Q,连结AQ,把△AOQ绕点O顺时针旋转一定的角度α(0°<α<360°),得到△A′OQ′,其中边A′Q′交坐标轴于点G.在旋转过程中,是否存在一点G,使得GQ′=OG?若存在,请直接写出所有满足条件的点Q′的坐标;若不存在,请说明理由.
(1)、填空:a= , 点B的坐标是;(2)、连结BD,点M是线段BD上一动点(点M不与端点B,D重合),过点M作MN⊥BD,交抛物线于点N(点N在对称轴的右侧),过点N作NH⊥x轴,垂足为H,交BD于点F,点P是y轴上一动点,当△MNF的周长取得最大值时,求FP+ PC的最小值;(3)、在(2)中,当△MNF的周长取得最大值时,FP+ PC取得最小值时,如图2,把点P向下平移 个单位得到点Q,连结AQ,把△AOQ绕点O顺时针旋转一定的角度α(0°<α<360°),得到△A′OQ′,其中边A′Q′交坐标轴于点G.在旋转过程中,是否存在一点G,使得GQ′=OG?若存在,请直接写出所有满足条件的点Q′的坐标;若不存在,请说明理由.