四川省眉山市2022年中考数学摸底试卷
试卷更新日期:2022-05-24 类型:中考模拟
一、单选题
-
1. 的倒数是()A、 B、 C、2022 D、2. 近年来,中国高铁发展迅速,高铁技术不断走出国门,成为展示我国实力的新名片.现在中国高速铁路营运里程将达到23000公里,将23000用科学记数法表示应为( )A、 B、 C、 D、3. 下列图案中,既是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 4. 下列长度的三条线段,能组成三角形的是( )A、3,4,8 B、5,6,10 C、5,5,11 D、5,6,115. 方差是刻画数据波动程度的量.对于一组数据 , , ,…, ,可用如下算式计算方差: ,其中“5”是这组数据的( )A、最小值 B、平均数 C、中位数 D、众数6. 一道来自课本的习题:
4. 下列长度的三条线段,能组成三角形的是( )A、3,4,8 B、5,6,10 C、5,5,11 D、5,6,115. 方差是刻画数据波动程度的量.对于一组数据 , , ,…, ,可用如下算式计算方差: ,其中“5”是这组数据的( )A、最小值 B、平均数 C、中位数 D、众数6. 一道来自课本的习题:从甲地到乙地有一段上坡与一段平路,如果保持上坡每小时走3km,平路每小时走4km,下坡每小时走5km,那么从甲地到乙地需54min,从乙地到甲地需42min,甲地到乙地全程是多少?
小红将这个实际问题转化为二元一次方程组问题,设未知数x,y,已经列出一个方程 ,则另一个方程正确的是( )
A、 B、 C、 D、7. 实数 在数轴上对应点的位置如图所示,则下列判断正确的是( )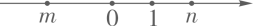 A、 B、 C、 D、8. 若关于x的一元二次方程 有实数根,则实数m的取值范围是( )A、 B、 C、 D、9. 如一次函数 与反比例函数 的图象如图所示,则二次函数 的大致图象是( )
A、 B、 C、 D、8. 若关于x的一元二次方程 有实数根,则实数m的取值范围是( )A、 B、 C、 D、9. 如一次函数 与反比例函数 的图象如图所示,则二次函数 的大致图象是( ) A、
A、 B、
B、 C、
C、 D、
D、 10. 如图,有两张矩形纸片 和 , , .把纸片 交叉叠放在纸片 上,使重叠部分为平行四边形,且点D与点G重合.当两张纸片交叉所成的角 最小时, 等于( )
10. 如图,有两张矩形纸片 和 , , .把纸片 交叉叠放在纸片 上,使重叠部分为平行四边形,且点D与点G重合.当两张纸片交叉所成的角 最小时, 等于( )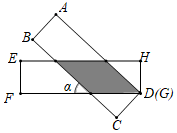 A、 B、 C、 D、11. 已知某函数的图象C与函数 的图象关于直线 对称.下列命题:①图象C与函数 的图象交于点 ;②点 在图象C上;③图象C上的点的纵坐标都小于4;④ , 是图象 上任意两点,若 ,则 .其中真命题是( )A、①② B、①③④ C、②③④ D、①②③④12. 如图是用8块A型瓷砖(白色四边形)和8块B型瓷砖(黑色三角形)不重叠、无空隙拼接而成的一个正方形图案,图案中A型瓷砖的总面积与B型瓷砖的总面积之比为( )
A、 B、 C、 D、11. 已知某函数的图象C与函数 的图象关于直线 对称.下列命题:①图象C与函数 的图象交于点 ;②点 在图象C上;③图象C上的点的纵坐标都小于4;④ , 是图象 上任意两点,若 ,则 .其中真命题是( )A、①② B、①③④ C、②③④ D、①②③④12. 如图是用8块A型瓷砖(白色四边形)和8块B型瓷砖(黑色三角形)不重叠、无空隙拼接而成的一个正方形图案,图案中A型瓷砖的总面积与B型瓷砖的总面积之比为( )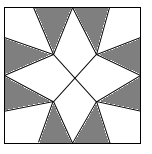 A、 :1 B、3:2 C、 :1 D、 :2
A、 :1 B、3:2 C、 :1 D、 :2二、填空题
-
13. 分解因式: .14. 若一个数的平方等于5,则这个数等于。
15. 一个不透明的布袋中仅有2个红球,1个黑球,这些球除颜色外无其它差别.先随机摸出一个小球,记下颜色后放回搅匀,再随机摸出一个小球,则两次摸出的小球颜色不同的概率是.16. 某活动小组购买4个篮球和5个足球,一共花费了466元,其中篮球的单价比足球的单价多4元,求篮球的单价和足球的单价.设篮球的单价为 元,足球的单价为 元,依题意,可列方程组为 .17. 如图,在Rt△ABC中,∠ACB=90°,AB=10,BC=6,CD∥AB,∠ABC的平分线BD交AC于点E,DE=. 18. 如图,由10个完全相同的正三角形构成的网格图中, 如图所示,则 =.
18. 如图,由10个完全相同的正三角形构成的网格图中, 如图所示,则 =.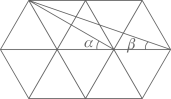
三、解答题
-
19. 计算: .20. 解方程: .21. 如图,⊙O中,弦 与 相交于点E, ,连接 .

求证:(1)、 ;(2)、 .22. 安全使用电瓶车可以大幅度减少因交通事故引发的人身伤害,为此交警部门在全市范围开展了安全使用电瓶车专项宣传活动.在活动前和活动后分别随机抽取了部分使用电瓶车的市民,就骑电瓶车戴安全帽情况进行问卷调查,将收集的数据制成如下统计图表.

活动前骑电瓶车戴安全帽情况统计表
类别
人数
A
68
B
245
C
510
D
177
合计
1000
(1)、宣传活动前,在抽取的市民中哪一类别的人数最多?占抽取人数的百分之几?(2)、该市约有30万人使用电瓶车,请估计活动前全市骑电瓶车“都不戴”安全帽的总人数;(3)、小明认为,宣传活动后骑电瓶车“都不戴”安全帽的人数为178,比活动前增加了1人,因此交警部门开展的宣传活动没有效果.小明分析数据的方法是否合理?请结合统计图表,对小明分析数据的方法及交警部门宣传活动的效果谈谈你的看法.23. 如图,在平面直角坐标系中,一次函数 的图象与反比例函数 的图象相交于第一、三象限内的 两点,与 轴交于点 . (1)、求该反比例函数和一次函数的解析式;(2)、在 轴上找一点 使 最大,求 的最大值及点 的坐标;(3)、直接写出当 时, 的取值范围.24. 如图,正方形ABCD的边长为2,E为AB的中点,P是BA延长线上的一点,连接PC交AD于点F,AP=FD.
(1)、求该反比例函数和一次函数的解析式;(2)、在 轴上找一点 使 最大,求 的最大值及点 的坐标;(3)、直接写出当 时, 的取值范围.24. 如图,正方形ABCD的边长为2,E为AB的中点,P是BA延长线上的一点,连接PC交AD于点F,AP=FD. (1)、求 的值;(2)、如图1,连接EC,在线段EC上取一点M,使EM=EB,连接MF,求证:MF=PF;(3)、如图2,过点E作EN⊥CD于点N,在线段EN上取一点Q,使AQ=AP,连接BQ,BN.将△AQB绕点A旋转,使点Q旋转后的对应点Q'落在边AD上.请判断点B旋转后的对应点B'是否落在线段BN上,并说明理由.25. 如图,已知直线 与抛物线C: 相交于 和点 两点.
(1)、求 的值;(2)、如图1,连接EC,在线段EC上取一点M,使EM=EB,连接MF,求证:MF=PF;(3)、如图2,过点E作EN⊥CD于点N,在线段EN上取一点Q,使AQ=AP,连接BQ,BN.将△AQB绕点A旋转,使点Q旋转后的对应点Q'落在边AD上.请判断点B旋转后的对应点B'是否落在线段BN上,并说明理由.25. 如图,已知直线 与抛物线C: 相交于 和点 两点. (1)、求抛物线C的函数表达式;(2)、若点M是位于直线 上方抛物线上的一动点,以 为相邻两边作平行四边形 ,当平行四边形 的面积最大时,求此时四边形 的面积S及点 的坐标;(3)、在抛物线C的对称轴上是否存在定点F,使抛物线C上任意一点P到点F的距离等于到直线 的距离,若存在,求出定点F的坐标;若不存在,请说明理由.
(1)、求抛物线C的函数表达式;(2)、若点M是位于直线 上方抛物线上的一动点,以 为相邻两边作平行四边形 ,当平行四边形 的面积最大时,求此时四边形 的面积S及点 的坐标;(3)、在抛物线C的对称轴上是否存在定点F,使抛物线C上任意一点P到点F的距离等于到直线 的距离,若存在,求出定点F的坐标;若不存在,请说明理由.