四川省乐山市五通桥区2022年中考数学模拟试卷

试卷更新日期：2022-05-24 类型：中考模拟

进入出卷网下载

一、单选题

1. $- 3 \frac{1}{2}$ 的相反数是（）

A、 $3 \frac{1}{2}$ B、 $\frac{2}{7}$ C、 $- \frac{2}{7}$ D、 $- \frac{7}{2}$

查看试题解析
2. 下列图形中，是轴对称图形，但不是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 芝麻被称为“八谷之冠”，是世界上最古老的油料作物之一．它作为食品和药物，得到广泛的使用．经测算，一粒芝麻的质量约为 $0.000 002 01$ kg，将100粒芝麻的质量用科学记数法表示约为（）

A、 $20.1 \times 10^{- 3}$ kg B、 $2.01 \times 10^{- 4}$ kg C、 $0.201 \times 10^{- 5}$ kg D、 $2.01 \times 10^{- 6}$ kg

查看试题解析
4. 将一张长方形纸片（足够长）折叠成如图所示图形，重叠部分是一个三角形（△ABC），BC为折痕，若∠1＝42°，则∠2的度数为（）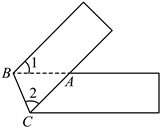

A、48° B、58° C、60° D、69°

查看试题解析
5. 下列调查中，适合用全面调查方式的是（）

A、了解一批灯泡的使用寿命 B、了解一批炮弹的杀伤半径 C、了解某班学生50米跑的成绩 D、了解一批袋装食品是否含有防腐剂

查看试题解析
6. 如图，AB是⊙O的直径， $\overset{⌢}{A C} = 3 \overset{⌢}{B C}$ ，则∠BAC的度数为（　　）

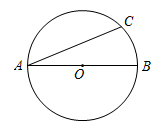A、22.5° B、30° C、45° D、67.5°

查看试题解析
7. 某厂今年3月的产值为50万元，5月份上升到72万元，这两个月平均每月增长的百分率是多少？若设平均每月增长的百分率为x，则列出的方程正确的是（）

A、50（1+x）=72 B、50（1+x）＋50（1+x）²=72 C、50（1+x）×2=72 D、50（1+x）²=72

查看试题解析
8. 如图，正方形ABCD的边长为3，点E，F分别在边BC，CD上，将AB，AD分别沿AE，AF折叠，点B，D恰好都落在点G处，已知BE＝1，则EF的长为（）

A、 $\frac{3}{2}$ B、 $\frac{5}{2}$ C、 $\frac{9}{4}$ D、3

查看试题解析
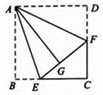9. 对于实数 $a ， b$ ，定义运算“*”； $a * b = {\begin{array}{l} a^{2} - a b (a \leq b) \\ b^{2} - a b (a > b) \end{array}$ 关于x的方程 $(2 x + 1) * (x - 1) = t$ 恰好有三个不相等的实数根，则t的取值范围是（）

A、 $- 2 < t < - \frac{1}{2}$ B、 $t > - \frac{1}{2}$ C、 $0 < t < 2 \frac{1}{4}$ D、 $- 2 \frac{1}{4} < t < 0$

查看试题解析
10. 如图1，在等边三角形ABC和矩形DEFG中，AC＝DE，点C，D，G都在直线l上，且AC⊥l于点C，DE⊥l于点D，且D，B，E三点共线，将矩形DEFG以每秒1个单位长度的速度从左向右匀速运动，直至矩形DEFG和△ABC无重叠部分，设矩形DEFG运动的时间为t秒，矩形DEFG和△ABC重叠部分的面积为S，图2为S随t的变化而变化的函数图象，则函数图象中点H的纵坐标是（）

A、 $\frac{4}{3} \sqrt{3}$ B、 $2 \sqrt{3}$ C、 $\frac{8}{3} \sqrt{3}$ D、3 $\sqrt{3}$

查看试题解析

二、填空题

11. 分解因式： $a^{3} - 4 a$ ＝.

查看试题解析
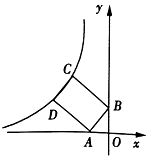
12. 不等式组 ${\begin{cases} x - 1 \geq 0 \\ 3 x - 6 < 0 \end{cases}$ 的整数解是.

查看试题解析
13. 若一组数据4，7，6，a，8的平均数为6，则这组数据的方差为.

查看试题解析
14. 在直径为10cm的⊙O中，弦AB的长为5 $\sqrt{2}$ cm，则AB所对的圆周角是．

查看试题解析
15. 如图，四边形ABCD是矩形，BC＝2AB，A，B两点的坐标分别是（﹣1，0），（0，1），C，D两点在反比例函数y＝ $\frac{k}{x}$ （x＜0）的图象上，则k的值是.

查看试题解析
16. 若 $m < - 1$ ，则下列函数① $y = \frac{m}{x} (x > 0)$ ；② $y = - m x + 1$ ；③ $y = m x$ ；④ $y = (m + 1) x$ 中，随x的增大而增大的是（填写编号）.

查看试题解析
17. 已知△ABC为直角三角形，它的内切圆的半径为2cm，两直角边的长分别是关于x的方程x²﹣17x+6m＝0的两个根，则△ABC的面积为（cm²）.

查看试题解析

三、解答题

18. 计算： $4 \sin 60 ° + {(- 2019)}^{0} - {(\frac{1}{2})}^{- 1} - | - 2 \sqrt{3} |$ ．

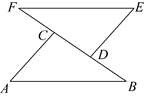
查看试题解析
19. 如图，点B，D，C，F在一条直线上，AB＝EF，AC＝ED，∠CAB＝∠DEF，求证：AC∥DE.

查看试题解析
20. 先化简，再求值： $\frac{x - 2}{x^{2} - 4 x + 4} \div (x + 2 - \frac{x^{2} + x - 4}{x - 2}) + \frac{1}{x + 1}$ ，其中 $x^{2} + x - 5 = 0$ .

查看试题解析
21.
中学生上学带手机的现象越来越受到社会的关注，为此媒体记者随机调查了某校若干名学生上学带手机的目的，分为四种类型：A接听电话；B收发短信；C查阅资料；D游戏聊天．并将调查结果绘制成图1和图2的统计图（不完整），请根据图中提供的信息，解答下列问题：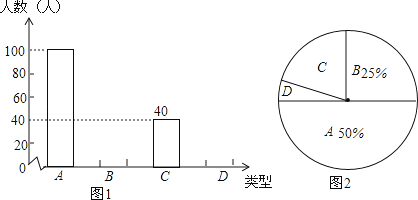

(1)、此次抽样调查中，共调查了名学生.

(2)、将图1、图2补充完整；

(3)、现有4名学生，其中A类两名，B类两名，从中任选2名学生，求这两名学生为同一类型的概率（用列表法或树状图法）．

查看试题解析
22. 如图，已知∠ABC=90°，AB=BC.直线l与以BC为直径的圆O相切于点C.点F是圆O上异于B、C的动点，直线BF与l相交于点E，过点F作AF的垂线交直线BC于点D.

(1)、如果BE=15，CE=9，求EF的长；

(2)、证明：①△CDF∽△BAF；②CD=CE；

(3)、探求动点F在什么位置时，相应的点D位于线段BC的延长线上，且使BC= $\sqrt{3}$ CD，请说明你的理由.

查看试题解析
23. 已知：△ABC内接于⊙O，过点B作⊙O的切线，交CA的延长线于点D，连接OB.

(1)、如图1，求证：∠DAB＝∠DBC；

(2)、如图2，过点D作DM⊥AB于点M，连接AO，交BC于点N，BM＝AM+AD，求证：BN＝CN；

(3)、如图3，在（2）的条件下，点E为⊙O上一点，过点E的切线交DB的延长线于点P，连接CE，交AO的延长线于点Q，连接PQ，PQ⊥OQ，点F为AN上一点，连接CF，若∠DCF+∠CDB＝90°，tan∠ECF＝2， $\frac{O N}{O Q} = \frac{1}{2}$ ，PQ+OQ＝6 $\sqrt{10}$ ，求CF的长.

查看试题解析
24. 已知二次函数y₁＝ax²+bx+c.

(1)、若二次函数y₁的图象经过A（﹣1，0），B（3，0），C（0，2），判定点D（2，2）是否在二次函数y₁的图象上；

(2)、一次函数y₂＝ax+b+c经过二次函数y₁的顶点.
①求二次函数y₁的对称轴；

②当b＜0，1＜x＜2时，比较y₁与y₂的大小.

查看试题解析
25. 如图1和图2，在平面直角坐标系中，点C的坐标为（0，4），A是x轴上的一个动点，M是线段AC的中点.把线段AM以A为旋转中心、按顺时针方向旋转90°得到AB.过B作x轴的垂线、过点C作y轴的垂线，两直线交于点D，直线DB交x轴于点E.设A点的横坐标为m.

(1)、求证：△AOC∽△BEA；

(2)、若m=3，则点B的坐标为；若m=﹣3，则点B的坐标为；

(3)、若m＞0，△BCD的面积为S，则m为何值时，S=6？

(4)、是否存在m，使得以B、C、D为顶点的三角形与△AOC相似？若存在，求此时m的值；若不存在，请说明理由.

查看试题解析
26. 如图1，在平面直角坐标系中，经过点D（﹣2，m）的抛物线y＝ax²+bx+4与x轴交于A（2，0），B（点B在点A的左侧）两点，AD交y轴正半轴于点E，过点D作DC⊥x轴于点C，AC＝DC.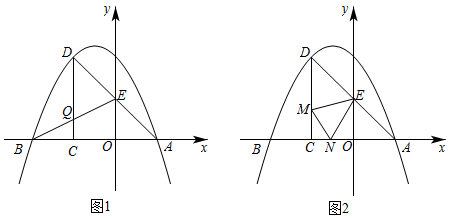

(1)、求抛物线的表达式.

(2)、连接BE交DC于点Q，抛物线上存在点P，满足PB＝PE，求点P的坐标.

(3)、如图2，M，N分别是线段DC，AC上的点，且∠MEN＝45°，连接MN，若△MCN中有一个锐角的正切值为2，直接写出S_△DME的值.

查看试题解析