四川省江油市2022年九年级下学期中考适应性考试数学试卷
试卷更新日期:2022-05-24 类型:中考模拟
一、单选题
-
1. 中国人最早使用负数,可追溯到两千多年前的秦汉时期,﹣0.5的相反数是( )A、0.5 B、±0.5 C、﹣0.5 D、52. 整式 的系数是( )A、-3 B、3 C、 D、3. 若 有意义,则a的取值范围是( )A、a≥1 B、a≤1 C、a≥0 D、a≤﹣14. 已知 , ,其中 , 为正整数,则 ( )A、 B、 C、 D、5. 如图,二次函数 的图象与 轴交于两点 , ,其中 .下列四个结论:① ;② ;③ ;④ ,正确的个数是( )
 A、1 B、2 C、3 D、46. 在平面直角坐标系中,以原点为对称中心,把点A(3,4)逆时针旋转90°,得到点B,则点B的坐标为( )A、(4,-3) B、(-4,3) C、(-3,4) D、(-3,-4)7. 近年来,网购的蓬勃发展方便了人们的生活.某快递分派站现有包裹若干件需快递员派送,若每个快递员派送10件,还剩6件;若每个快递员派送12件,还差6件,那么该分派站现有包裹( )A、60件 B、66件 C、68件 D、72件8. 下列运算正确的是( )A、a2.a3=a6 B、a3+a2=a5 C、(a2)4=a8 D、a3-a2=a9. 甲、乙二人同驾一辆车出游,各匀速行驶一半路程,共用3小时,到达目的地后,甲对乙说:“我用你所花的时间,可以行驶180km”,乙对甲说:“我用你所花的时间,只能行驶80km”.从他们的交谈中可以判断,乙驾车的时长为( )A、1.2小时 B、1.6小时 C、1.8小时 D、2小时10. 已知x是整数,当 取最小值时,x的值是( )A、5 B、6 C、7 D、811. 将全体正奇数排成一个三角形数阵
A、1 B、2 C、3 D、46. 在平面直角坐标系中,以原点为对称中心,把点A(3,4)逆时针旋转90°,得到点B,则点B的坐标为( )A、(4,-3) B、(-4,3) C、(-3,4) D、(-3,-4)7. 近年来,网购的蓬勃发展方便了人们的生活.某快递分派站现有包裹若干件需快递员派送,若每个快递员派送10件,还剩6件;若每个快递员派送12件,还差6件,那么该分派站现有包裹( )A、60件 B、66件 C、68件 D、72件8. 下列运算正确的是( )A、a2.a3=a6 B、a3+a2=a5 C、(a2)4=a8 D、a3-a2=a9. 甲、乙二人同驾一辆车出游,各匀速行驶一半路程,共用3小时,到达目的地后,甲对乙说:“我用你所花的时间,可以行驶180km”,乙对甲说:“我用你所花的时间,只能行驶80km”.从他们的交谈中可以判断,乙驾车的时长为( )A、1.2小时 B、1.6小时 C、1.8小时 D、2小时10. 已知x是整数,当 取最小值时,x的值是( )A、5 B、6 C、7 D、811. 将全体正奇数排成一个三角形数阵1
3 5
7 9 11
13 15 17 19
21 23 25 27 29
… … … … … …
根据以上排列规律,数阵中第25行的第20个数是( )
A、639 B、637 C、635 D、63312. “赶陀螺”是一项深受人们喜爱的运动.如图所示是一个陀螺的立体结构图.已知底面圆的直径AB=8 cm,圆柱的高BC=6 cm,圆锥的高CD=3 cm,则这个陀螺的表面积是( )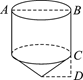 A、68π cm2 B、74π cm2 C、84π cm2 D、100π cm2
A、68π cm2 B、74π cm2 C、84π cm2 D、100π cm2二、填空题
-
13. 因式分解: 。14. 若多项式 是关于x,y的三次多项式,则 .15. 如图, , 的平分线与 的平分线交于点E,则 .
 16. 如图,将平行四边形ABCO放置在平面直角坐标系xOy中,O为坐标原点,若点A的坐标是(6,0),点C的坐标是(1,4),则点B的坐标是 .
16. 如图,将平行四边形ABCO放置在平面直角坐标系xOy中,O为坐标原点,若点A的坐标是(6,0),点C的坐标是(1,4),则点B的坐标是 .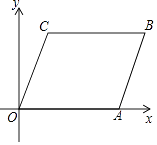 17. 在直角 中, , , 的角平分线交 于点 ,且 ,斜边 的值是.18. 若不等式 >﹣x﹣ 的解都能使不等式(m﹣6)x<2m+1成立,则实数m的取值范围是 .
17. 在直角 中, , , 的角平分线交 于点 ,且 ,斜边 的值是.18. 若不等式 >﹣x﹣ 的解都能使不等式(m﹣6)x<2m+1成立,则实数m的取值范围是 .三、解答题
-
19.(1)、计算: ;(2)、先化简,再求值: ,其中 , .20. 4月23日是“世界读书日”,甲、乙两个书店在这一天举行了购书优惠活动.甲书店:所有书籍按标价8折出售;乙书店:一次购书中标价总额不超过100元的按原价计费,超过100元后的部分打6折.(1)、以x(单位:元)表示标价总额,y(单位:元)表示应支付金额,分别就两家书店的优惠方式,求y关于x的函数解析式;(2)、“世界读书日”这一天,如何选择这两家书店去购书更省钱?21. 辰星旅游度假村有甲种风格客房15间,乙种风格客房20间.按现有定价:若全部入住,一天营业额为8500元;若甲、乙两种风格客房均有10间入住,一天营业额为5000元.(1)、求甲、乙两种客房每间现有定价分别是多少元?(2)、度假村以乙种风格客房为例,市场情况调研发现:若每个房间每天按现有定价,房间会全部住满;当每个房间每天的定价每增加20元时,就会有两个房间空闲.如果游客居住房间,度假村需对每个房间每天支出80元的各种费用.当每间房间定价为多少元时,乙种风格客房每天的利润m最大,最大利润是多少元?22. 如图,已知△ABC的顶点坐标分别为A(3,0),B(0,4),C(-3,0)。动点M,N同时从A点出发,M沿A→C,N沿折线A→B→C,均以每秒1个单位长度的速度移动,当一个动点到达终点C时,另一个动点也随之停止移动,移动时间记为t秒。连接MN。
 (1)、求直线BC的解析式;(2)、移动过程中,将△AMN沿直线MN翻折,点A恰好落在BC边上点D处,求此时t值及点D的坐标;(3)、当点M,N移动时,记△ABC在直线MN右侧部分的面积为S,求S关于时间t的函数关系式。23. 如图,AB是⊙O 的直径,点D在⊙O 上(点D不与A,B重合),直线AD交过点B的切线于点C,过点D作⊙O 的切线DE交BC于点E.
(1)、求直线BC的解析式;(2)、移动过程中,将△AMN沿直线MN翻折,点A恰好落在BC边上点D处,求此时t值及点D的坐标;(3)、当点M,N移动时,记△ABC在直线MN右侧部分的面积为S,求S关于时间t的函数关系式。23. 如图,AB是⊙O 的直径,点D在⊙O 上(点D不与A,B重合),直线AD交过点B的切线于点C,过点D作⊙O 的切线DE交BC于点E. (1)、求证:BE=CE;(2)、若DE平行AB,求sin∠ACO 的值.24. 如图,设反比例函数的解析式为y= (k>0).
(1)、求证:BE=CE;(2)、若DE平行AB,求sin∠ACO 的值.24. 如图,设反比例函数的解析式为y= (k>0).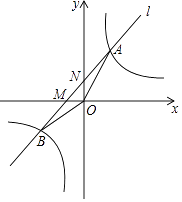 (1)、若该反比例函数与正比例函数y=2x的图象有一个交点的纵坐标为2,求k的值;(2)、若该反比例函数与过点M(﹣2,0)的直线l:y=kx+b的图象交于A,B两点,如图所示,当△ABO的面积为 时,求直线l的解析式.25. 如图,二次函数y=﹣x2﹣2x+4﹣a2的图象与一次函数y=﹣2x的图象交于点A、B(点B在右侧),与y轴交于点C,点A的横坐标恰好为a.动点P、Q同时从原点O出发,沿射线OB分别以每秒 和2 个单位长度运动,经过t秒后,以PQ为对角线作矩形PMQN,且矩形四边与坐标轴平行.
(1)、若该反比例函数与正比例函数y=2x的图象有一个交点的纵坐标为2,求k的值;(2)、若该反比例函数与过点M(﹣2,0)的直线l:y=kx+b的图象交于A,B两点,如图所示,当△ABO的面积为 时,求直线l的解析式.25. 如图,二次函数y=﹣x2﹣2x+4﹣a2的图象与一次函数y=﹣2x的图象交于点A、B(点B在右侧),与y轴交于点C,点A的横坐标恰好为a.动点P、Q同时从原点O出发,沿射线OB分别以每秒 和2 个单位长度运动,经过t秒后,以PQ为对角线作矩形PMQN,且矩形四边与坐标轴平行. (1)、求a的值及t=1秒时点P的坐标;(2)、当矩形PMQN与抛物线有公共点时,求时间t的取值范围;(3)、在位于x轴上方的抛物线图象上任取一点R,作关于原点(0,0)的对称点为R′,当点M恰在抛物线上时,求R′M长度的最小值,并求此时点R的坐标.
(1)、求a的值及t=1秒时点P的坐标;(2)、当矩形PMQN与抛物线有公共点时,求时间t的取值范围;(3)、在位于x轴上方的抛物线图象上任取一点R,作关于原点(0,0)的对称点为R′,当点M恰在抛物线上时,求R′M长度的最小值,并求此时点R的坐标.